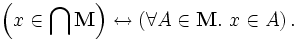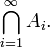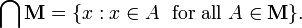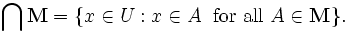Intersection (set theory)
Background to the schools Wikipedia
The articles in this Schools selection have been arranged by curriculum topic thanks to SOS Children volunteers. SOS Child sponsorship is cool!
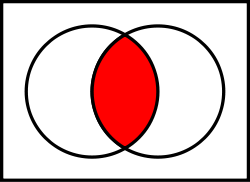
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements.
For explanation of the symbols used in this article, refer to the table of mathematical symbols.
Basic definition
The intersection of A and B is written "A ∩ B". Formally:
- x is an element of A ∩ B if and only if
- x is an element of A and
- x is an element of B.
- For example:
- The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
- The number 9 is not in the intersection of the set of prime numbers {2, 3, 5, 7, 11, …} and the set of odd numbers {1, 3, 5, 7, 9, 11, …}.
If the intersection of two sets A and B is empty, that is they have no elements in common, then they are said to be disjoint, denoted: A ∩ B = Ø. For example the sets {1, 2} and {3, 4} are disjoint, written
{1, 2} ∩ {3, 4} = Ø.
More generally, one can take the intersection of several sets at once. The intersection of A, B, C, and D, for example, is A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)). Intersection is an associative operation; thus,
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
Arbitrary intersections
The most general notion is the intersection of an arbitrary nonempty collection of sets. If M is a nonempty set whose elements are themselves sets, then x is an element of the intersection of M if and only if for every element A of M, x is an element of A. In symbols:
This idea subsumes the above paragraphs, in that for example, A ∩ B ∩ C is the intersection of the collection {A,B,C}.
The notation for this last concept can vary considerably. Set theorists will sometimes write "∩M", while others will instead write "∩A∈M A". The latter notation can be generalized to "∩i∈I Ai", which refers to the intersection of the collection {Ai : i ∈ I}. Here I is a nonempty set, and Ai is a set for every i in I.
In the case that the index set I is the set of natural numbers, you might see notation analogous to that of an infinite series:
When formatting is difficult, this can also be written "A1 ∩ A2 ∩ A3 ∩ ...", even though strictly speaking, A1 ∩ (A2 ∩ (A3 ∩ ... makes no sense. (This last example, an intersection of countably many sets, is actually very common; for an example see the article on σ-algebras.)
Finally, let us note that whenever the symbol "∩" is placed before other symbols instead of between them, it should be of a larger size (⋂).
Nullary intersection
Note that in the previous section we excluded the case where M was the empty set (∅). The reason is as follows. The intersection of the collection M is defined as the set (see set-builder notation)
If M is empty there are no sets A in M, so the question becomes "which x's satisfy the stated condition?" The answer seems to be every possible x. When M is empty the condition given above is an example of a vacuous truth. So the intersection of the empty family should be the "set of everything". The problem is, there is no such set. Assuming such a set exists leads to a famous problem in naive set theory known as Russell's paradox. For this reason the intersection of the empty set is left undefined.
A partial fix for this problem can be found if we agree to restrict our attention to subsets of a fixed set U called the universe. In this case the intersection of a family of subsets of U can be defined as
Now if M is empty there is no problem. The intersection is just the entire universe U, which is a well-defined set by assumption.