
File:Golden mean.png
Size of this preview: 480 × 480 pixels.
| |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help. |
Summary
| Description |
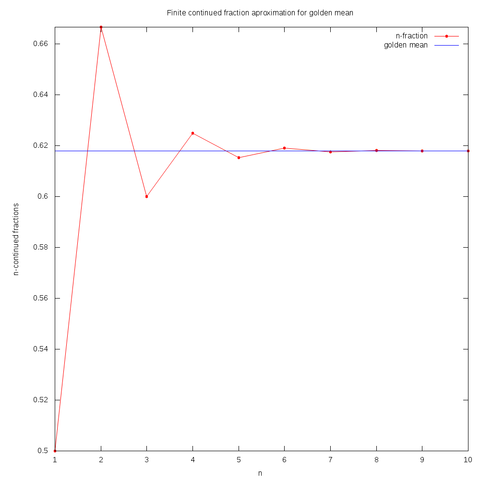
English: Approximation of golden mean by finite continued fractions :
|
| Date | 21 October 2011 |
| Source | Own work |
| Author | Adam majewski |
Licensing
|
Maxima CAS src code
/* golden ratio conjugate = ((sqrt(5)-1)/2 = 0.618033988749895 It is approximated by finite continued fractions : [0;1,1,1,....] */ kill(all); iMax : 10; /* continuead fraction - goldem mean */ f(i_Max):= ( [a,i], i:1, a:[0,1,1], while iWe have helped children in Africa for many years - you can help too...
