Adding and Subtracting Radical Expressions

8.3 Adding and Subtracting Radical Expressions

Learning Objectives

Add and subtract like radicals.
Simplify radical expressions involving like radicals.

Adding and Subtracting Radical Expressions

Adding and subtracting radical expressions is similar to adding and subtracting like terms. Radicals are considered to be like radicalsRadicals that share the same index and radicand., or similar radicalsTerm used when referring to like radicals., when they share the same index and radicand. For example, the terms $3 \sqrt{5}$ and $4 \sqrt{5}$ contain like radicals and can be added using the distributive property as follows:

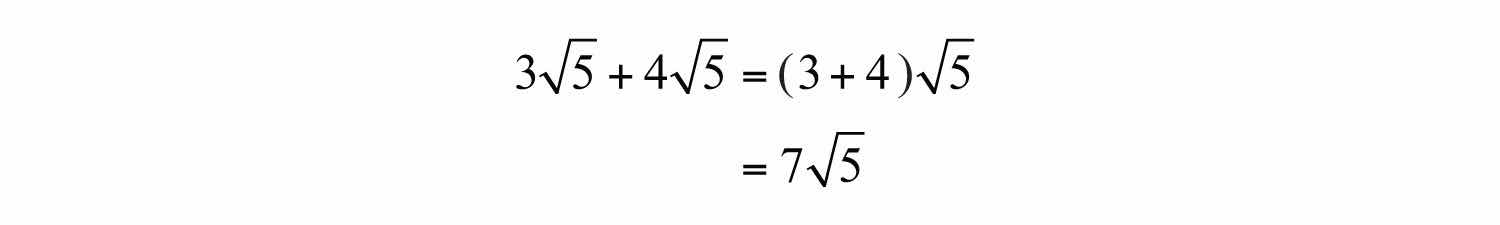
Typically, we do not show the step involving the distributive property and simply write

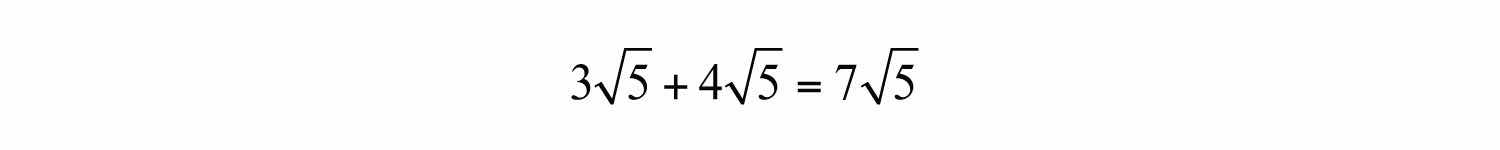
When adding terms with like radicals, add only the coefficients; the radical part remains the same.

Example 1: Add: $3 \sqrt{2} + 2 \sqrt{2}$ .

Solution: The terms contain like radicals; therefore, add the coefficients.

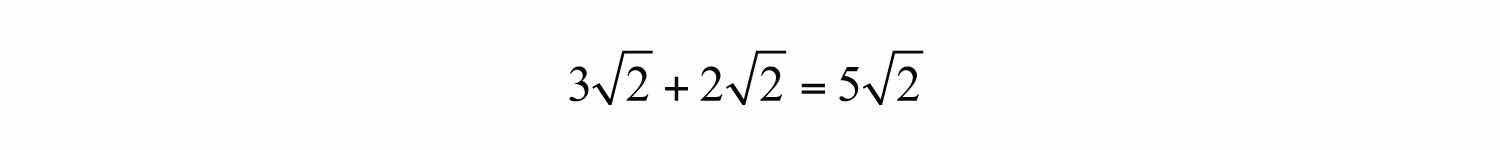
Answer: $5 \sqrt{2}$

Subtraction is performed in a similar manner.

Example 2: Subtract: $2 \sqrt{7} - 3 \sqrt{7}$ .

Solution:

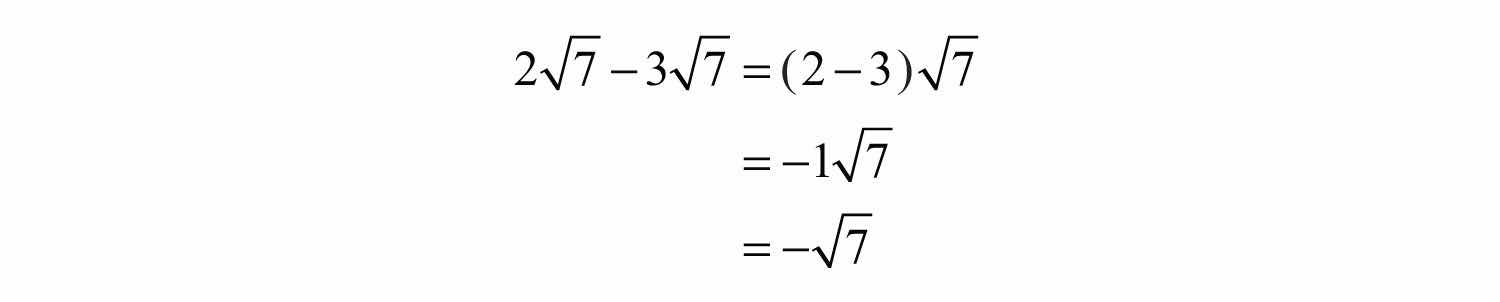
Answer: $- \sqrt{7}$

If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.

Example 3: Simplify: $10 \sqrt{5} + 6 \sqrt{2} - 9 \sqrt{5} - 7 \sqrt{2}$ .

Solution:

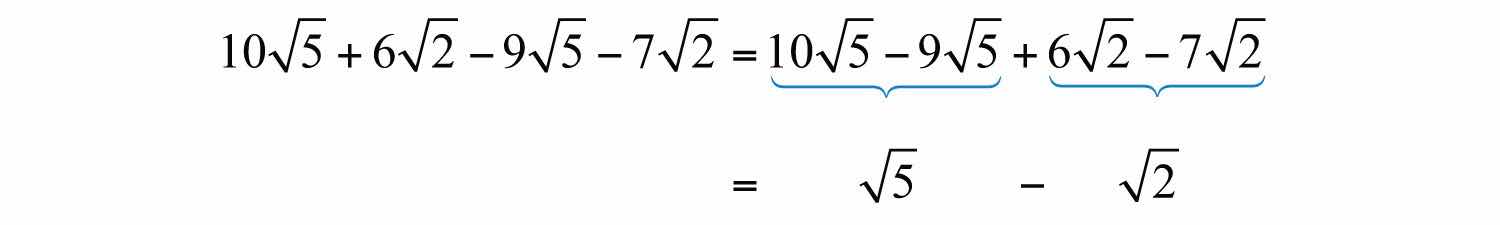
We cannot simplify any further because $\sqrt{5}$ and $\sqrt{2}$ are not like radicals; the radicands are not the same.

Answer: $\sqrt{5} - \sqrt{2}$

Caution

It is important to point out that $\sqrt{5} - \sqrt{2} \neq \sqrt{5 - 2}$ . We can verify this by calculating the value of each side with a calculator.

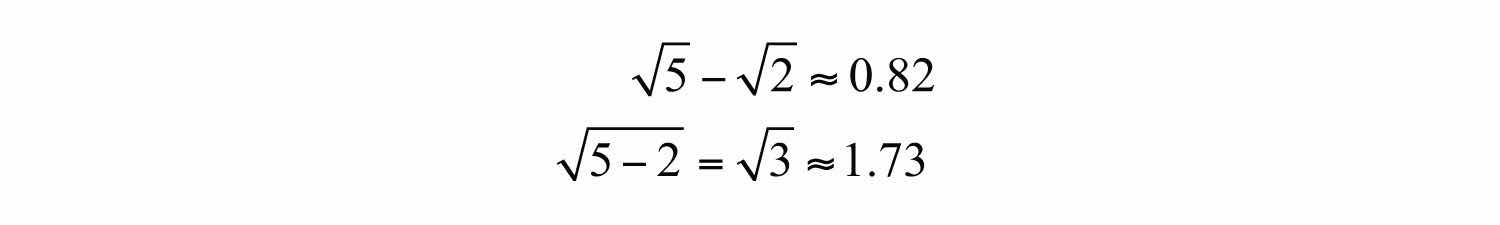
In general, note that $\sqrt[n]{a} \pm \sqrt[n]{b} \neq \sqrt[n]{a \pm b}$ .

Example 4: Simplify: $3 \sqrt[3]{6} + 2 \sqrt{6} - \sqrt[3]{6} - 3 \sqrt{6}$ .

Solution:

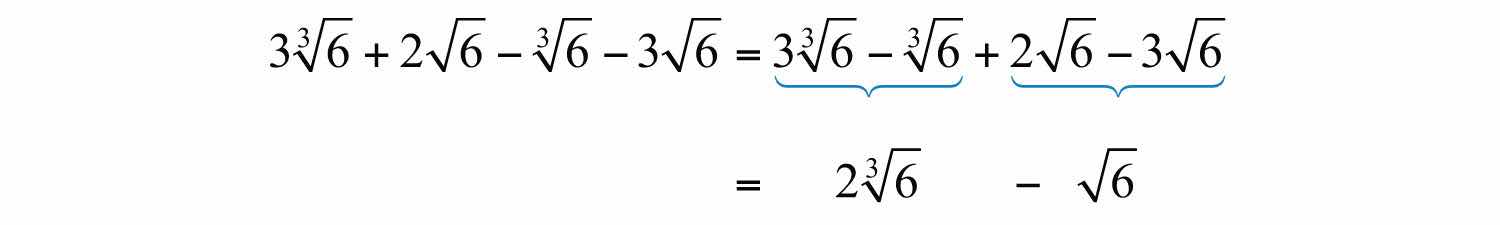
We cannot simplify any further because $\sqrt[3]{6}$ and $\sqrt{6}$ are not like radicals; the indices are not the same.

Answer: $2 \sqrt[3]{6} - \sqrt{6}$

Often we will have to simplify before we can identify the like radicals within the terms.

Example 5: Subtract: $\sqrt{12} - \sqrt{48}$ .

Solution: At first glance, the radicals do not appear to be similar. However, after simplifying completely, we will see that we can combine them.

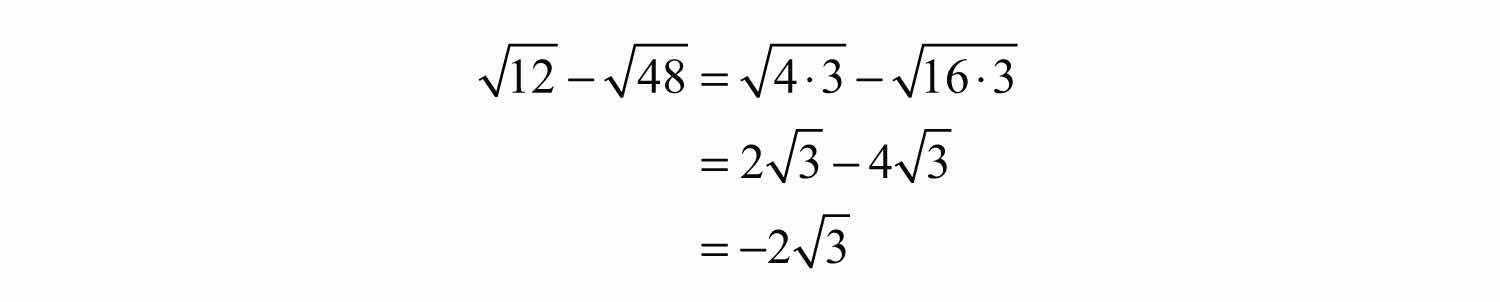
Answer: $- 2 \sqrt{3}$

Example 6: Simplify: $\sqrt{20} + \sqrt{27} - 3 \sqrt{5} - 2 \sqrt{12}$ .

Solution:

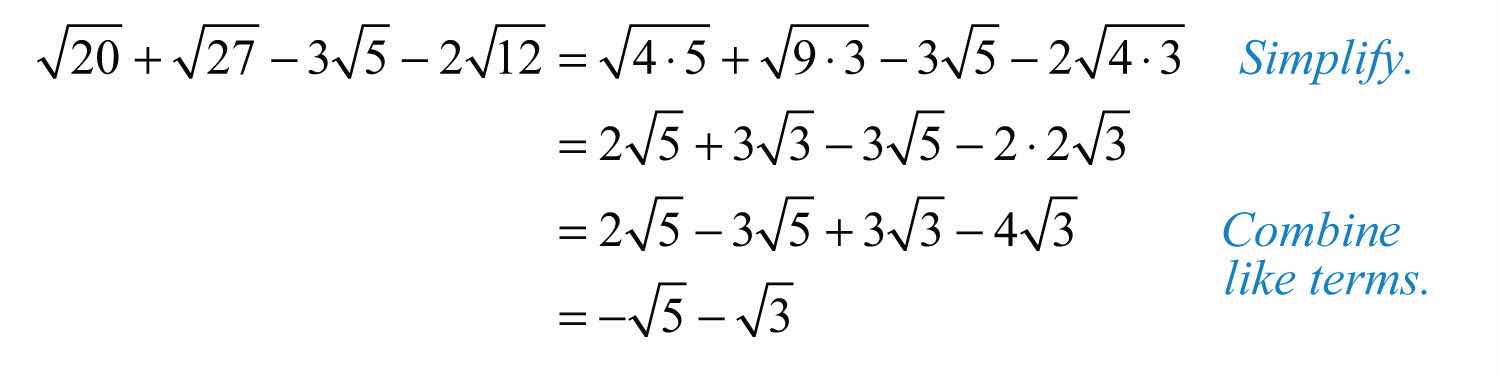
Answer: $- \sqrt{5} - \sqrt{3}$

Try this! Subtract: $2 \sqrt{50} - 6 \sqrt{8}$ .

Answer: $- 2 \sqrt{2}$

Video Solution

(click to see video)

Next, we work with radical expressions involving variables. In this section, assume all radicands containing variable expressions are not negative.

Example 7: Simplify: $- 6 \sqrt[3]{2 x} - \sqrt[3]{3 x} + 7 \sqrt[3]{2 x}$ .

Solution:

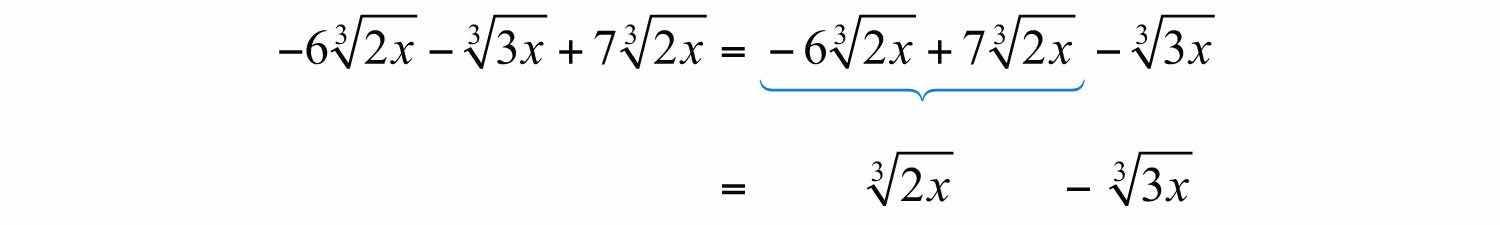
We cannot combine any further because the remaining radical expressions do not share the same radicand; they are not like radicals. Note that $\sqrt[3]{2 x} - \sqrt[3]{3 x} \neq \sqrt[3]{2 x - 3 x}$ .

Answer: $\sqrt[3]{2 x} - \sqrt[3]{3 x}$

We will often find the need to subtract a radical expression with multiple terms. If this is the case, remember to apply the distributive property before combining like terms.

Example 8: Simplify: $(9 \sqrt{x} - 2 \sqrt{y}) - (10 \sqrt{x} + 7 \sqrt{y})$ .

Solution:

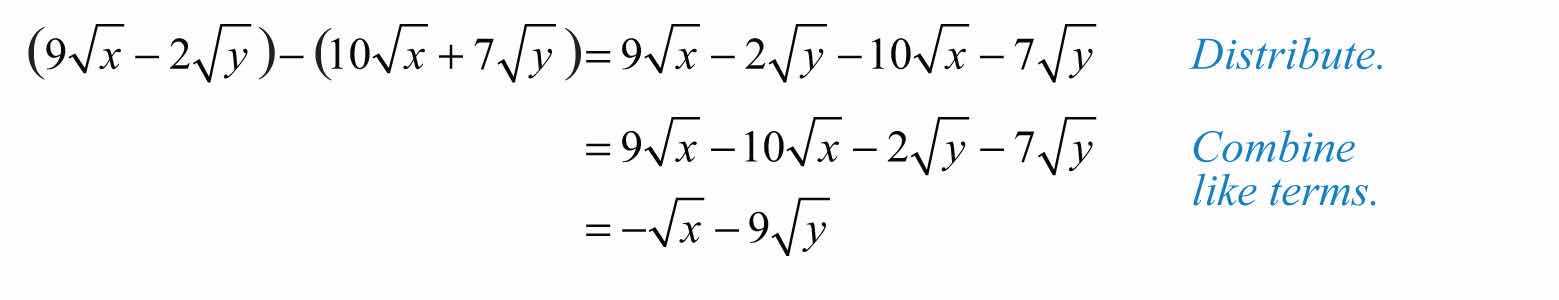
Answer: $- \sqrt{x} - 9 \sqrt{y}$

Until we simplify, it is often unclear which terms involving radicals are similar.

Example 9: Simplify: $5 \sqrt[3]{2 y} - (\sqrt[3]{54 y} - \sqrt[3]{16})$ .

Solution:

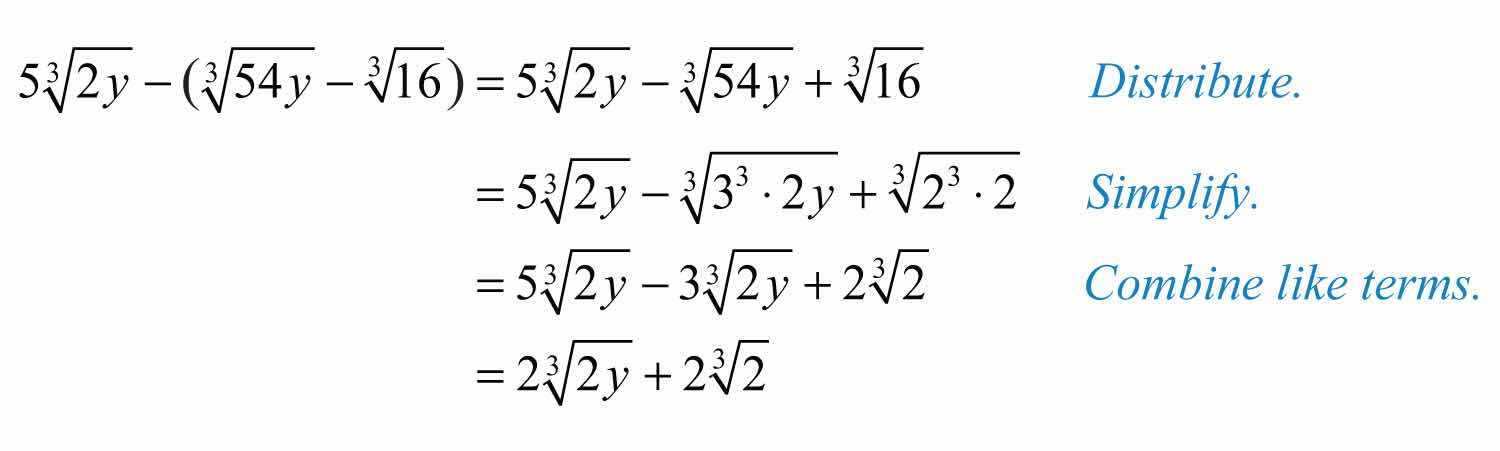
Answer: $2 \sqrt[3]{2 y} + 2 \sqrt[3]{2}$

Example 10: Simplify: $2 a \sqrt{125 a^{2} b} - a^{2} \sqrt{80 b} + 4 \sqrt{20 a^{4} b}$ .

Solution:

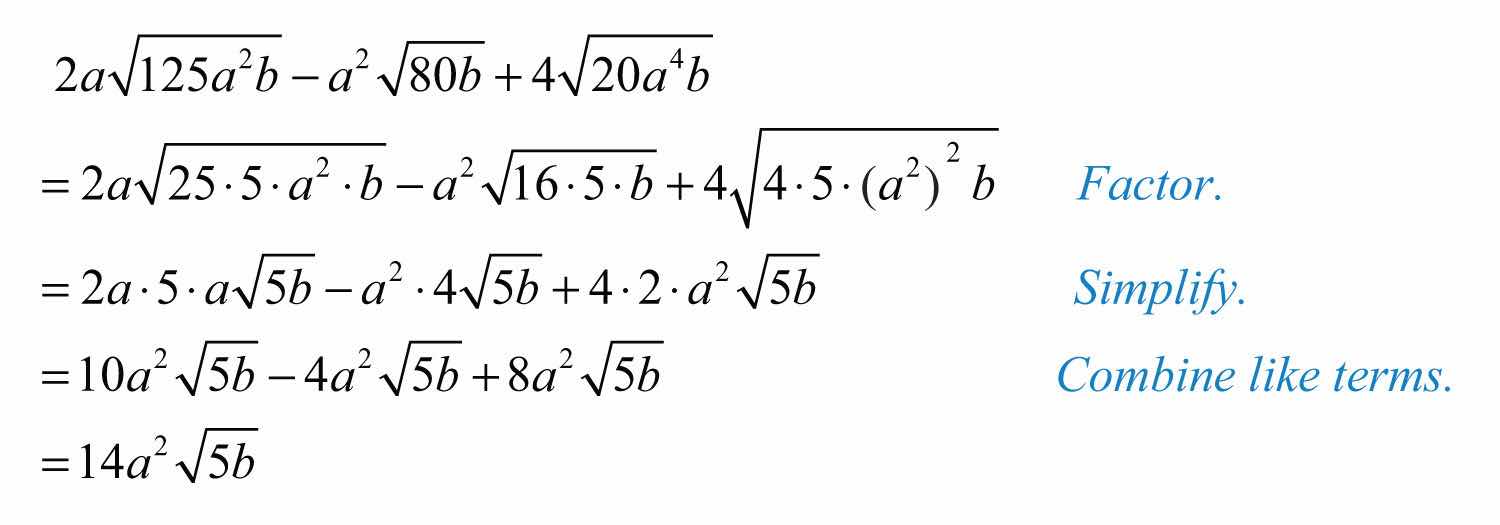
Answer: $14 a^{2} \sqrt{5 b}$

Try this! Simplify: $\sqrt{45 x^{3}} - (\sqrt{20 x^{3}} - \sqrt{80 x})$ .

Answer: $x \sqrt{5 x} + 4 \sqrt{5 x}$

Video Solution

(click to see video)

Tip

Take careful note of the differences between products and sums within a radical.

Products	Sums
$\begin{array}{l} \sqrt{x^{2} y^{2}} = x y \\ \sqrt[3]{x^{3} y^{3}} = x y \end{array}$	$\begin{array}{l} \sqrt{x^{2} + y^{2}} \neq x + y \\ \sqrt[3]{x^{3} + y^{3}} \neq x + y \end{array}$

The property $\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}$ says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.

Key Takeaways

Add and subtract terms that contain like radicals just as you do like terms. If the index and radicand are exactly the same, then the radicals are similar and can be combined. This involves adding or subtracting only the coefficients; the radical part remains the same.
Simplify each radical completely before combining like terms.

Topic Exercises

Part A: Adding and Subtracting Like Radicals

Simplify.

1. $9 \sqrt{3} + 5 \sqrt{3}$

2. $12 \sqrt{6} + 3 \sqrt{6}$

3. $4 \sqrt{5} - 7 \sqrt{5}$

4. $3 \sqrt{10} - 8 \sqrt{10}$

5. $\sqrt{6} - 4 \sqrt{6} + 2 \sqrt{6}$

6. $5 \sqrt{10} - 15 \sqrt{10} - 2 \sqrt{10}$

7. $13 \sqrt{7} - 6 \sqrt{2} - 5 \sqrt{7} + 5 \sqrt{2}$

8. $10 \sqrt{13} - 12 \sqrt{15} + 5 \sqrt{13} - 18 \sqrt{15}$

9. $6 \sqrt{5} - (4 \sqrt{3} - 3 \sqrt{5})$

10. $- 12 \sqrt{2} - (6 \sqrt{6} + \sqrt{2})$

11. $(2 \sqrt{5} - 3 \sqrt{10}) - (\sqrt{10} + 3 \sqrt{5})$

12. $(- 8 \sqrt{3} + 6 \sqrt{15}) - (\sqrt{3} - \sqrt{15})$

13. $4 \sqrt[3]{6} - 3 \sqrt[3]{5} + 6 \sqrt[3]{6}$

14. $\sqrt[3]{10} + 5 \sqrt[3]{10} - 4 \sqrt[3]{10}$

15. $(7 \sqrt[3]{9} - 4 \sqrt[3]{3}) - (\sqrt[3]{9} - 3 \sqrt[3]{3})$

16. $(- 8 \sqrt[3]{5} + \sqrt[3]{25}) - (2 \sqrt[3]{5} + 6 \sqrt[3]{25})$

Simplify. (Assume all radicands containing variable expressions are positive.)

17. $9 \sqrt{x} + 7 \sqrt{x}$

18. $- 8 \sqrt{y} + 4 \sqrt{y}$

19. $7 x \sqrt{y} - 3 x \sqrt{y} + x \sqrt{y}$

20. $10 y^{2} \sqrt{x} - 12 y^{2} \sqrt{x} - 2 y^{2} \sqrt{x}$

21. $2 \sqrt{a b} - 5 \sqrt{a} + 6 \sqrt{a b} - 10 \sqrt{a}$

22. $- 3 x \sqrt{y} + 6 \sqrt{y} - 4 x \sqrt{y} - 7 \sqrt{y}$

23. $5 \sqrt{x y} - (3 \sqrt{x y} - 7 \sqrt{x y})$

24. $- 8 a \sqrt{b} - (2 a \sqrt{b} - 4 \sqrt{a b})$

25. $(3 \sqrt{2 x} - \sqrt{3 x}) - (\sqrt{2 x} - 7 \sqrt{3 x})$

26. $(\sqrt{y} - 4 \sqrt{2 y}) - (\sqrt{y} - 5 \sqrt{2 y})$

27. $5 \sqrt[3]{x} - 12 \sqrt[3]{x}$

28. $- 2 \sqrt[3]{y} - 3 \sqrt[3]{y}$

29. $a \cdot \sqrt[5]{3 b} + 4 a \cdot \sqrt[5]{3 b} - a \cdot \sqrt[5]{3 b}$

30. $- 8 \sqrt[4]{a b} + 3 \sqrt[4]{a b} - 2 \sqrt[4]{a b}$

31. $6 \sqrt{2 a} - 4 \sqrt[3]{2 a} + 7 \sqrt{2 a} - \sqrt[3]{2 a}$

32. $4 \sqrt[5]{3 a} + \sqrt[3]{3 a} - 9 \sqrt[5]{3 a} + \sqrt[3]{3 a}$

33. $(\sqrt[4]{4 x y} - \sqrt[3]{x y}) - (2 \sqrt[4]{4 x y} - \sqrt[3]{x y})$

34. $(5 \sqrt[6]{6 y} - 5 \sqrt{y}) - (2 \sqrt[6]{6 y} + 3 \sqrt{y})$

Part B: Adding and Subtracting Rational Expressions

Simplify.

35. $\sqrt{75} - \sqrt{12}$

36. $\sqrt{24} - \sqrt{54}$

37. $\sqrt{32} + \sqrt{27} - \sqrt{8}$

38. $\sqrt{20} + \sqrt{48} - \sqrt{45}$

39. $\sqrt{28} - \sqrt{27} + \sqrt{63} - \sqrt{12}$

40. $\sqrt{90} + \sqrt{24} - \sqrt{40} - \sqrt{54}$

41. $\sqrt{45} - \sqrt{80} + \sqrt{245} - \sqrt{5}$

42. $\sqrt{108} + \sqrt{48} - \sqrt{75} - \sqrt{3}$

43. $4 \sqrt{2} - (\sqrt{27} - \sqrt{72})$

44. $- 3 \sqrt{5} - (\sqrt{20} - \sqrt{50})$

45. $\sqrt[3]{16} - \sqrt[3]{54}$

46. $\sqrt[3]{81} - \sqrt[3]{24}$

47. $\sqrt[3]{135} + \sqrt[3]{40} - \sqrt[3]{5}$

48. $\sqrt[3]{108} - \sqrt[3]{32} - \sqrt[3]{4}$

49. $2 \sqrt{27} - 2 \sqrt{12}$

50. $3 \sqrt{50} - 4 \sqrt{32}$

51. $3 \sqrt{243} - 2 \sqrt{18} - \sqrt{48}$

52. $6 \sqrt{216} - 2 \sqrt{24} - 2 \sqrt{96}$

53. $2 \sqrt{18} - 3 \sqrt{75} - 2 \sqrt{98} + 4 \sqrt{48}$

54. $2 \sqrt{45} - \sqrt{12} + 2 \sqrt{20} - \sqrt{108}$

55. $(2 \sqrt{363} - 3 \sqrt{96}) - (7 \sqrt{12} - 2 \sqrt{54})$

56. $(2 \sqrt{288} + 3 \sqrt{360}) - (2 \sqrt{72} - 7 \sqrt{40})$

57. $3 \sqrt[3]{54} + 5 \sqrt[3]{250} - 4 \sqrt[3]{16}$

58. $4 \sqrt[3]{162} - 2 \sqrt[3]{384} - 3 \sqrt[3]{750}$

Simplify. (Assume all radicands containing variable expressions are positive.)

59. $\sqrt{81 b} + \sqrt{4 b}$

60. $\sqrt{100 a} + \sqrt{a}$

61. $\sqrt{9 a^{2} b} - \sqrt{36 a^{2} b}$

62. $\sqrt{50 a^{2}} - \sqrt{18 a^{2}}$

63. $\sqrt{49 x} - \sqrt{9 y} + \sqrt{x} - \sqrt{4 y}$

64. $\sqrt{9 x} + \sqrt{64 y} - \sqrt{25 x} - \sqrt{y}$

65. $7 \sqrt{8 x} - (3 \sqrt{16 y} - 2 \sqrt{18 x})$

66. $2 \sqrt{64 y} - (3 \sqrt{32 y} - \sqrt{81 y})$

67. $2 \sqrt{9 m^{2} n} - 5 m \sqrt{9 n} + \sqrt{m^{2} n}$

68. $4 \sqrt{18 n^{2} m} - 2 n \sqrt{8 m} + n \sqrt{2 m}$

69. $\sqrt{4 x^{2} y} - \sqrt{9 x y^{2}} - \sqrt{16 x^{2} y} + \sqrt{y^{2} x}$

70. $\sqrt{32 x^{2} y^{2}} + \sqrt{12 x^{2} y} - \sqrt{18 x^{2} y^{2}} - \sqrt{27 x^{2} y}$

71. $(\sqrt{9 x^{2} y} - \sqrt{16 y}) - (\sqrt{49 x^{2} y} - 4 \sqrt{y})$

72. $(\sqrt{72 x^{2} y^{2}} - \sqrt{18 x^{2} y}) - (\sqrt{50 x^{2} y^{2}} + x \sqrt{2 y})$

73. $\sqrt{12 m^{4} n} - m \sqrt{75 m^{2} n} + 2 \sqrt{27 m^{4} n}$

74. $5 n \sqrt{27 m n^{2}} + 2 \sqrt{12 m n^{4}} - n \sqrt{3 m n^{2}}$

75. $2 \sqrt{27 a^{3} b} - a \sqrt{48 a b} - a \sqrt{144 a^{3} b}$

76. $2 \sqrt{98 a^{4} b} - 2 a \sqrt{162 a^{2} b} + a \sqrt{200 b}$

77. $\sqrt[3]{125 a} - \sqrt[3]{27 a}$

78. $\sqrt[3]{1000 a^{2}} - \sqrt[3]{64 a^{2}}$

79. $2 x \cdot \sqrt[3]{54 x} - 2 \sqrt[3]{16 x^{4}} + 5 \sqrt[3]{2 x^{4}}$

80. $x \cdot \sqrt[3]{54 x^{3}} - \sqrt[3]{250 x^{6}} + x^{2} \cdot \sqrt[3]{2}$

81. $\sqrt[4]{16 y^{2}} + \sqrt[4]{81 y^{2}}$

82. $\sqrt[5]{32 y^{4}} - \sqrt[5]{y^{4}}$

83. $\sqrt[4]{32 a^{3}} - \sqrt[4]{162 a^{3}} + 5 \sqrt[4]{2 a^{3}}$

84. $\sqrt[4]{80 a^{4} b} + \sqrt[4]{5 a^{4} b} - a \cdot \sqrt[4]{5 b}$

85. $\sqrt[3]{27 x^{3}} + \sqrt[3]{8 x} - \sqrt[3]{125 x^{3}}$

86. $\sqrt[3]{24 x} - \sqrt[3]{128 x} - \sqrt[3]{81 x}$

87. $\sqrt[3]{27 x^{4} y} - \sqrt[3]{8 x y^{3}} + x \cdot \sqrt[3]{64 x y} - y \cdot \sqrt[3]{x}$

88. $\sqrt[3]{125 x y^{3}} + \sqrt[3]{8 x^{3} y} - \sqrt[3]{216 x y^{3}} + 10 x \cdot \sqrt[3]{y}$

89. $(\sqrt[3]{162 x^{4} y} - \sqrt[3]{250 x^{4} y^{2}}) - (\sqrt[3]{2 x^{4} y^{2}} - \sqrt[3]{384 x^{4} y})$

90. $(\sqrt[5]{32 x^{2} y^{6}} - \sqrt[5]{243 x^{6} y^{2}}) - (\sqrt[5]{x^{2} y^{6}} - x \cdot \sqrt[5]{x y^{2}})$

Part C: Discussion Board

91. Choose values for x and y and use a calculator to show that $\sqrt{x + y} \neq \sqrt{x} + \sqrt{y}$ .

92. Choose values for x and y and use a calculator to show that $\sqrt{x^{2} + y^{2}} \neq x + y$ .

Answers

1: $14 \sqrt{3}$

3: $- 2 \sqrt{5}$

5: $- \sqrt{6}$

7: $8 \sqrt{7} - \sqrt{2}$

9: $9 \sqrt{5} - 4 \sqrt{3}$

11: $- \sqrt{5} - 4 \sqrt{10}$

13: $10 \sqrt[3]{6} - 3 \sqrt[3]{5}$

15: $6 \sqrt[3]{9} - \sqrt[3]{3}$

17: $16 \sqrt{x}$

19: $5 x \sqrt{y}$

21: $8 \sqrt{a b} - 15 \sqrt{a}$

23: $9 \sqrt{x y}$

25: $2 \sqrt{2 x} + 6 \sqrt{3 x}$

27: $- 7 \sqrt[3]{x}$

29: $4 a \cdot \sqrt[5]{3 b}$

31: $13 \sqrt{2 a} - 5 \sqrt[3]{2 a}$

33: $- \sqrt[4]{4 x y}$

35: $3 \sqrt{3}$

37: $2 \sqrt{2} + 3 \sqrt{3}$

39: $5 \sqrt{7} - 5 \sqrt{3}$

41: $5 \sqrt{5}$

43: $10 \sqrt{2} - 3 \sqrt{3}$

45: $- \sqrt[3]{2}$

47: $4 \sqrt[3]{5}$

49: $2 \sqrt{3}$

51: $23 \sqrt{3} - 6 \sqrt{2}$

53: $- 8 \sqrt{2} + \sqrt{3}$

55: $8 \sqrt{3} - 6 \sqrt{6}$

57: $26 \sqrt[3]{2}$

59: $11 \sqrt{b}$

61: $- 3 a \sqrt{b}$

63: $8 \sqrt{x} - 5 \sqrt{y}$

65: $20 \sqrt{2 x} - 12 \sqrt{y}$

67: $- 8 m \sqrt{n}$

69: $- 2 x \sqrt{y} - 2 y \sqrt{x}$

71: $- 4 x \sqrt{y}$

73: $3 m^{2} \sqrt{3 n}$

75: $2 a \sqrt{3 a b} - 12 a^{2} \sqrt{a b}$

77: $2 \sqrt[3]{a}$

79: $7 x \cdot \sqrt[3]{2 x}$

81: $5 \sqrt[4]{y^{2}}$

83: $4 \sqrt[4]{2 a^{3}}$

85: $- 2 x + 2 \sqrt[3]{x}$

87: $7 x \cdot \sqrt[3]{x y} - 3 y \cdot \sqrt[3]{x}$

89: $7 x \cdot \sqrt[3]{6 x y} - 6 x \cdot \sqrt[3]{2 x y^{2}}$