Adding and subtracting rational expressions is similar to adding and subtracting fractions. Recall that if the denominators are the same, we can add or subtract the numerators and write the result over the common denominator.
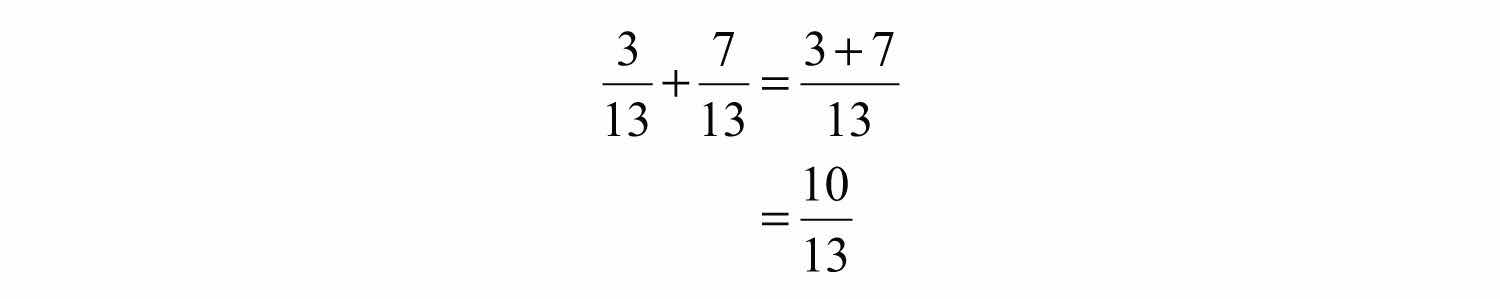
When working with rational expressions, the common denominator will be a polynomial. In general, given polynomials P, Q, and R, where , we have the following:
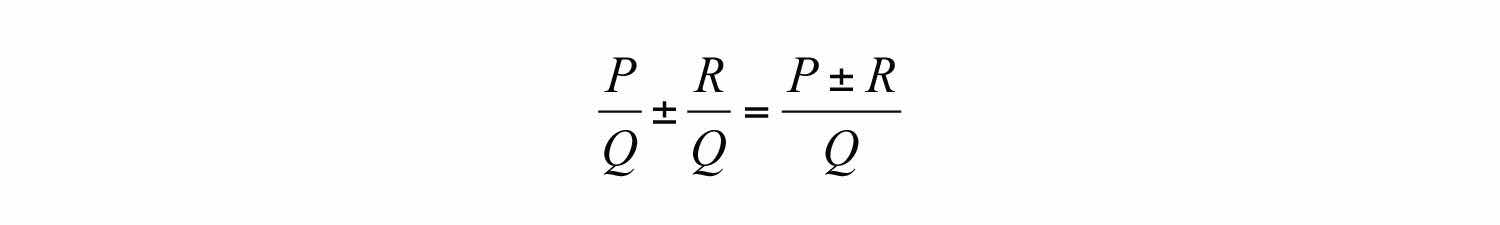
In this section, assume that all variable factors in the denominator are nonzero.
Example 1: Add: .
Solution: Add the numerators 3 and 7, and write the result over the common denominator, y.
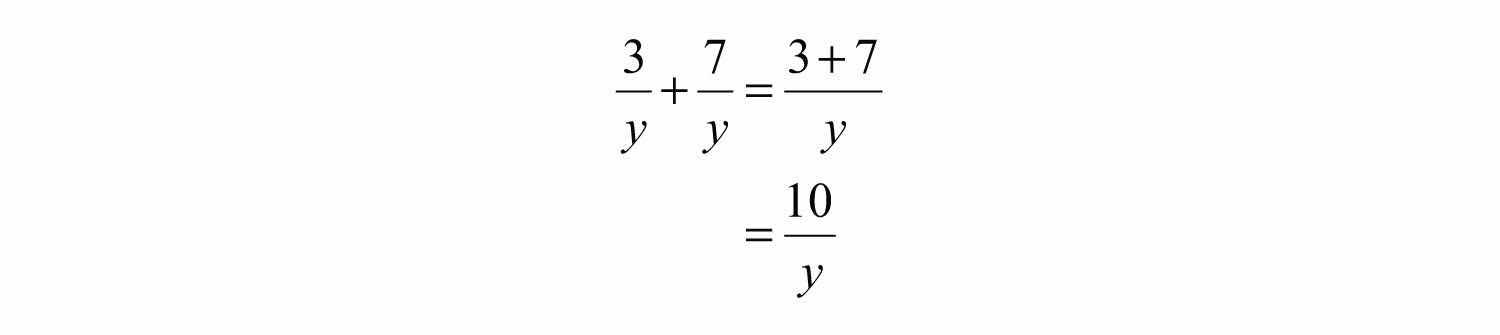
Answer:
Example 2: Subtract: .
Solution: Subtract the numerators and 1, and write the result over the common denominator, .
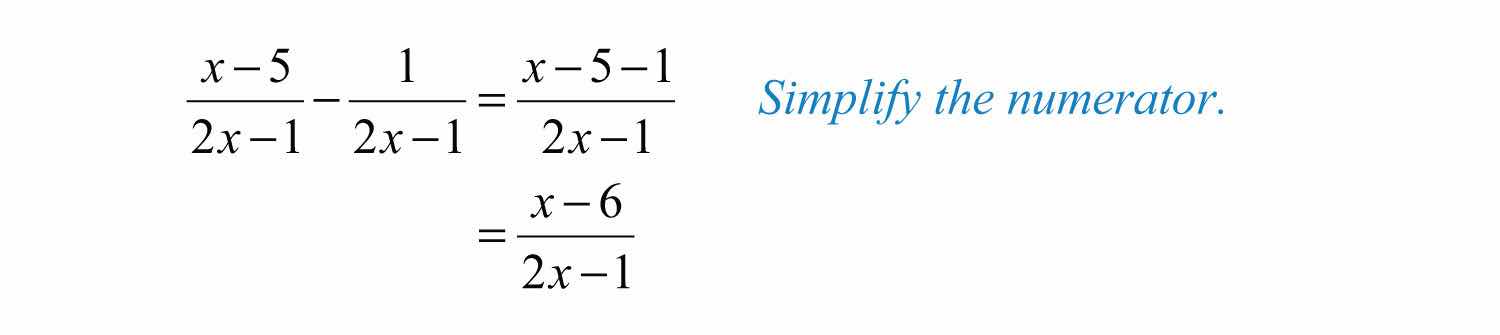
Answer:
Example 3: Subtract: .
Solution: We use parentheses to remind us to subtract the entire numerator of the second rational expression.
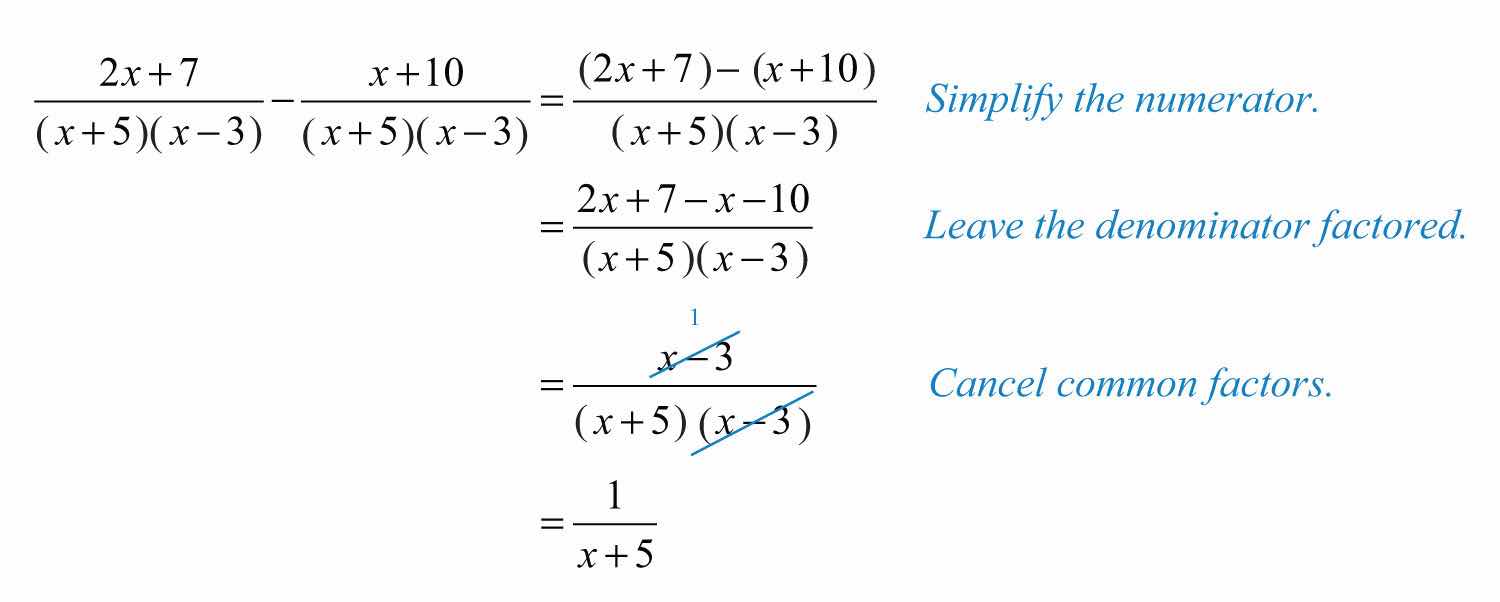
Answer:
Example 4: Simplify: .
Solution: Subtract and add the numerators. Make use of parentheses and write the result over the common denominator, .
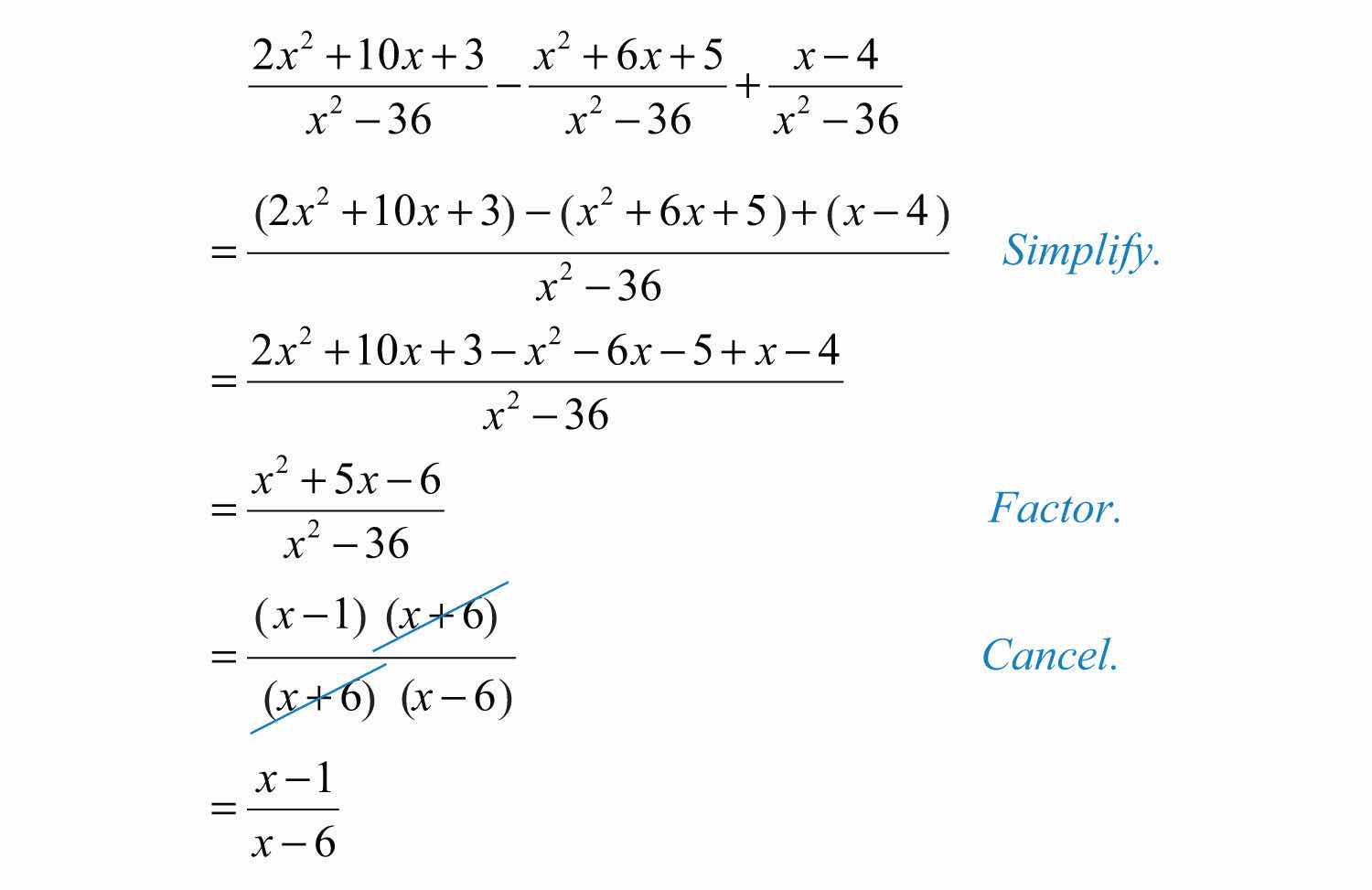
Answer:
Try this! Subtract: .
Answer:
To add rational expressions with unlike denominators, first find equivalent expressions with common denominators. Do this just as you have with fractions. If the denominators of fractions are relatively prime, then the least common denominator (LCD) is their product. For example,
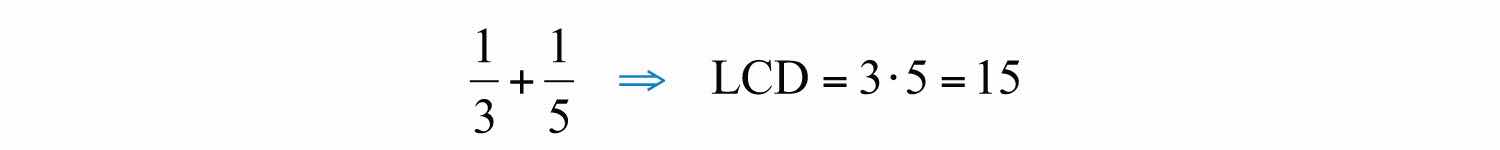
Multiply each fraction by the appropriate form of 1 to obtain equivalent fractions with a common denominator.

The process of adding and subtracting rational expressions is similar. In general, given polynomials P, Q, R, and S, where and , we have the following:
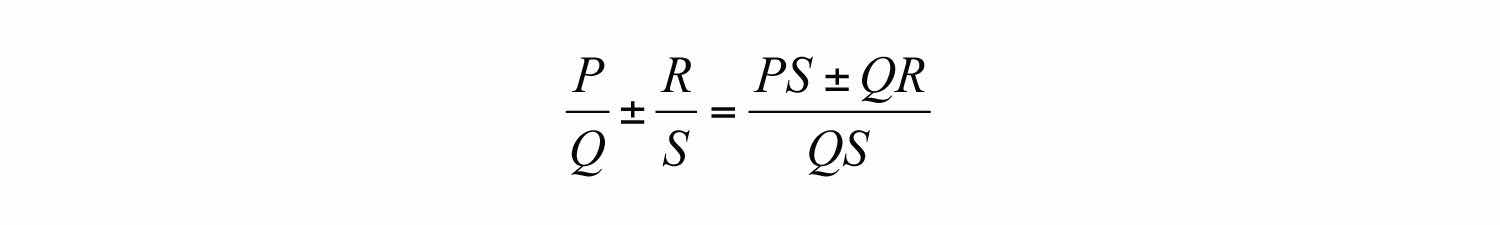
In this section, assume that all variable factors in the denominator are nonzero.
Example 5: Add: .
Solution: In this example, the . To obtain equivalent terms with this common denominator, multiply the first term by and the second term by .

Answer:
Example 6: Subtract: .
Solution: Since the , multiply the first term by 1 in the form of and the second term by .
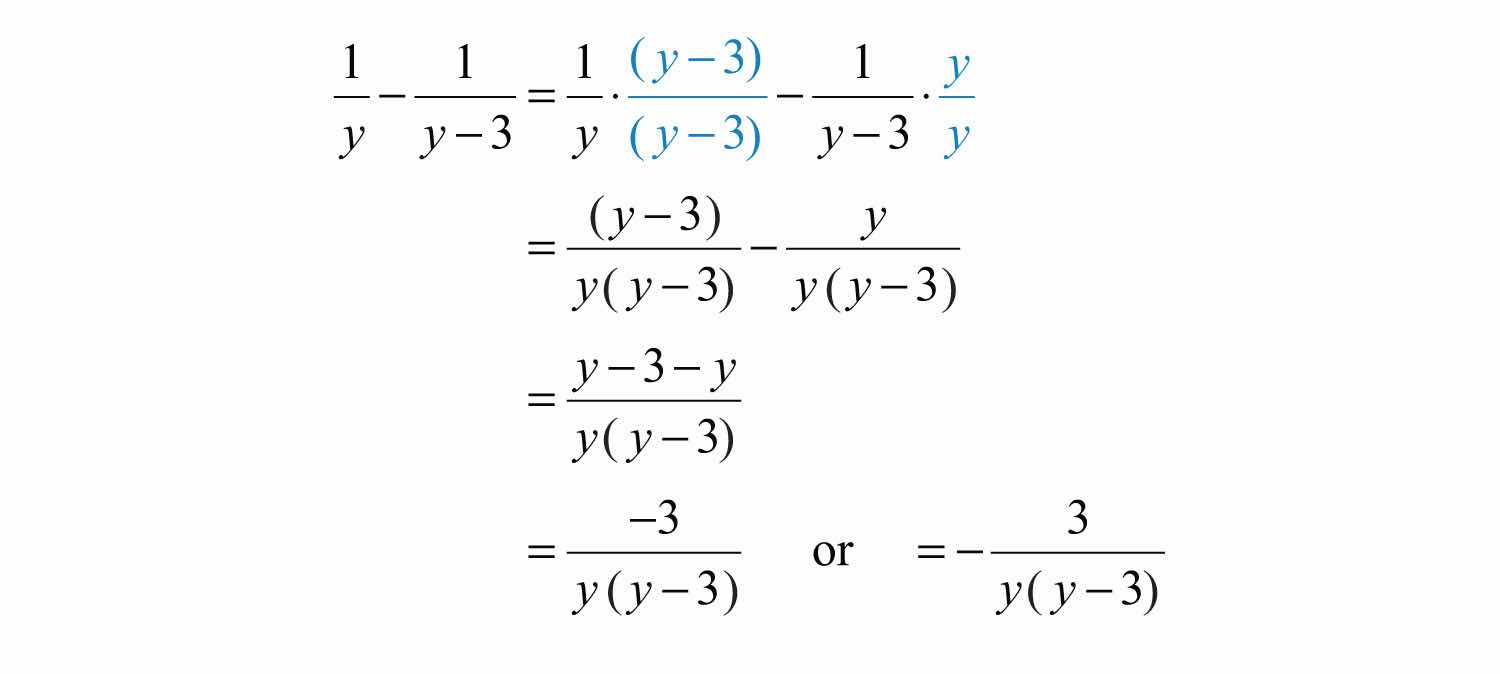
Answer:
It is not always the case that the LCD is the product of the given denominators. Typically, the denominators are not relatively prime; thus determining the LCD requires some thought. Begin by factoring all denominators. The LCD is the product of all factors with the highest power. For example, given
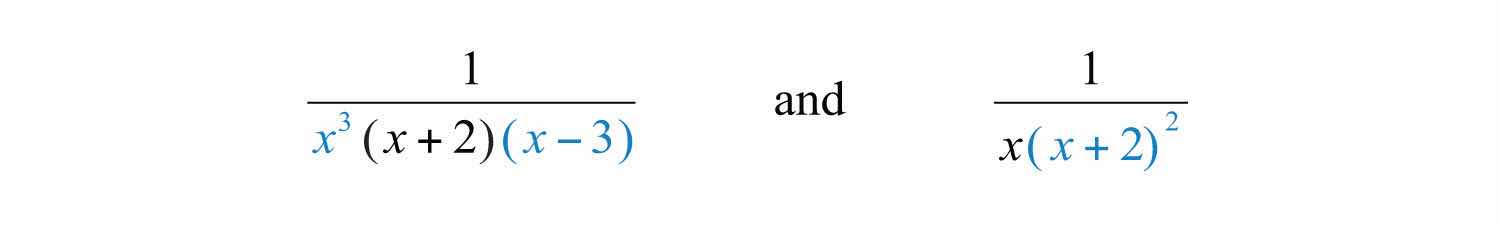
there are three base factors in the denominator: , , and . The highest powers of these factors are , , and . Therefore,
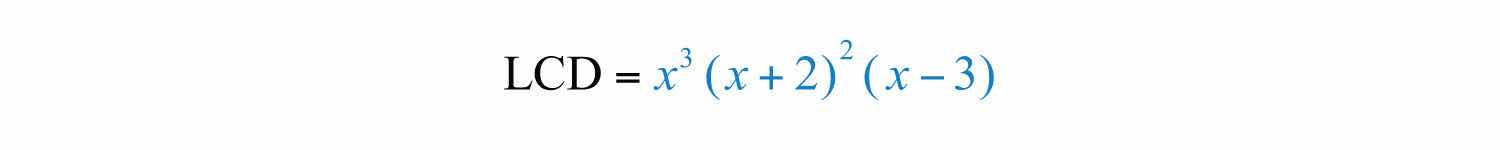
The general steps for adding or subtracting rational expressions are illustrated in the following example.
Example 7: Subtract: .
Solution:
Step 1: Factor all denominators to determine the LCD.
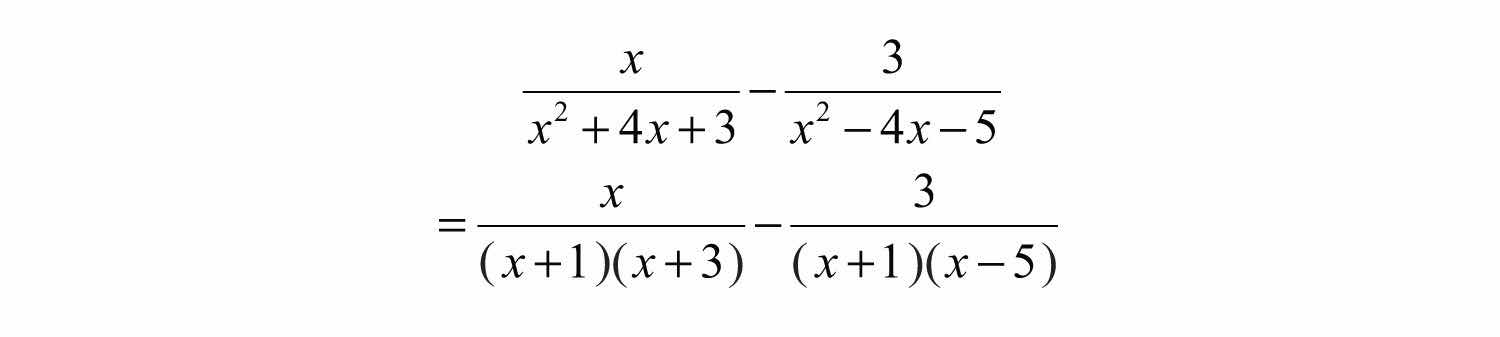
The .
Step 2: Multiply by the appropriate factors to obtain equivalent terms with a common denominator. To do this, multiply the first term by and the second term by .
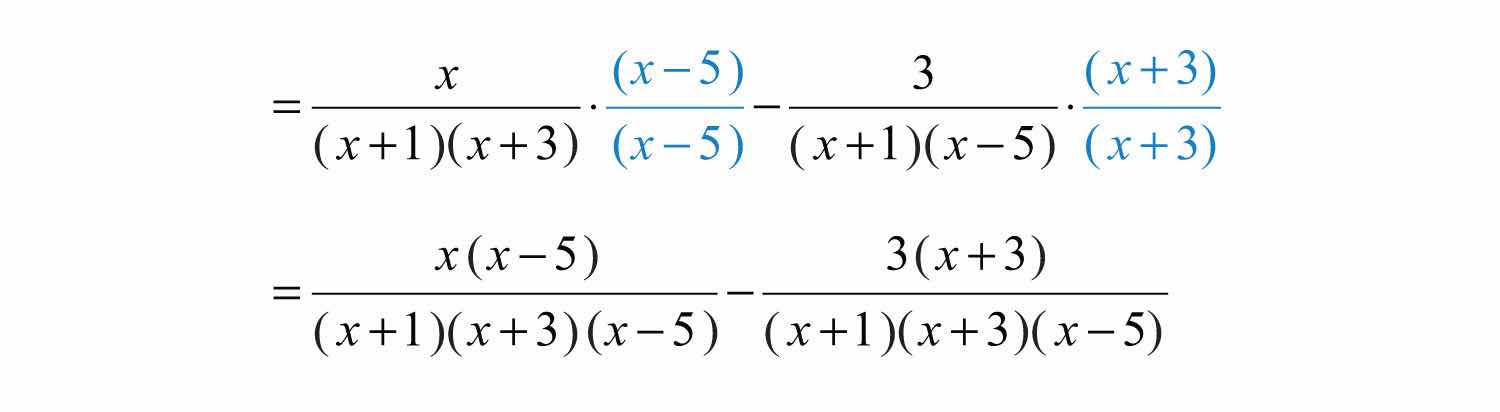
Step 3: Add or subtract the numerators and place the result over the common denominator.
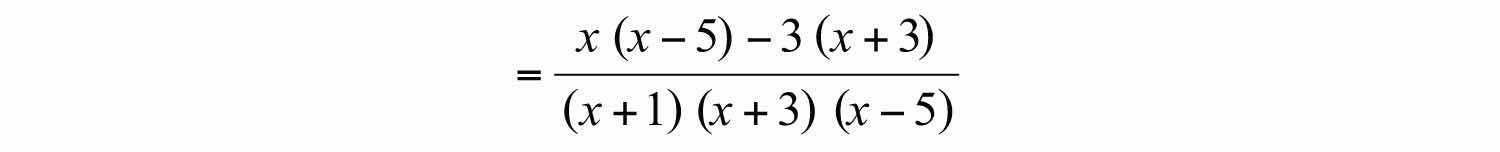
Step 4: Simplify the resulting algebraic fraction.

Answer:
Example 8: Subtract: .
Solution: It is best not to factor the numerator, , because we will most likely need to simplify after we subtract.

Answer:
Example 9: Subtract: .
Solution: First, factor the denominators and determine the LCD. Notice how the opposite binomial property is applied to obtain a more workable denominator.
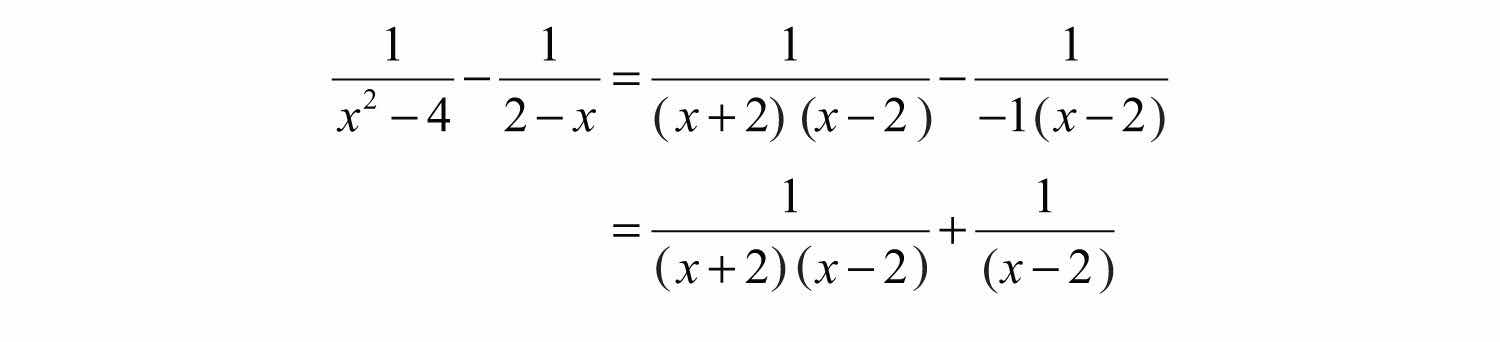
The LCD is . Multiply the second term by 1 in the form of .
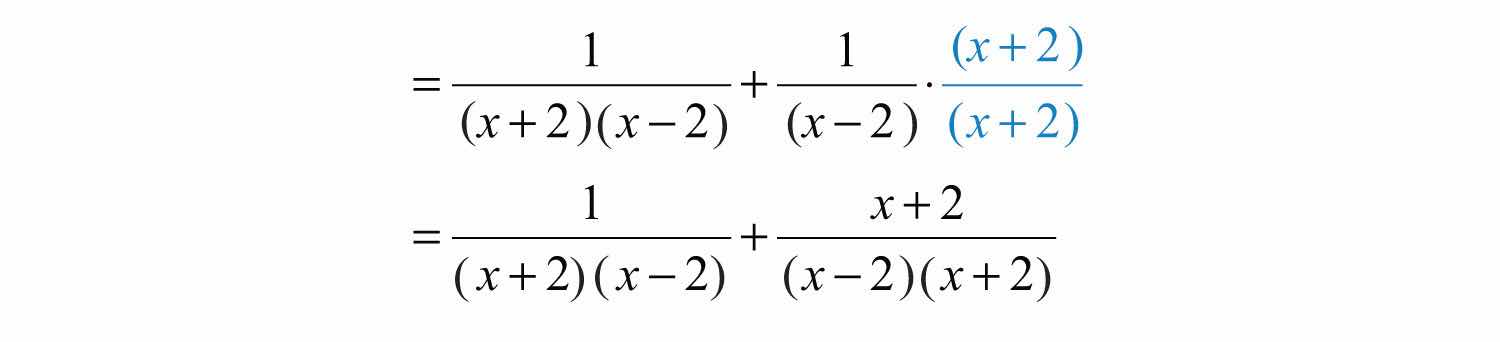
Now that we have equivalent terms with a common denominator, add the numerators and write the result over the common denominator.
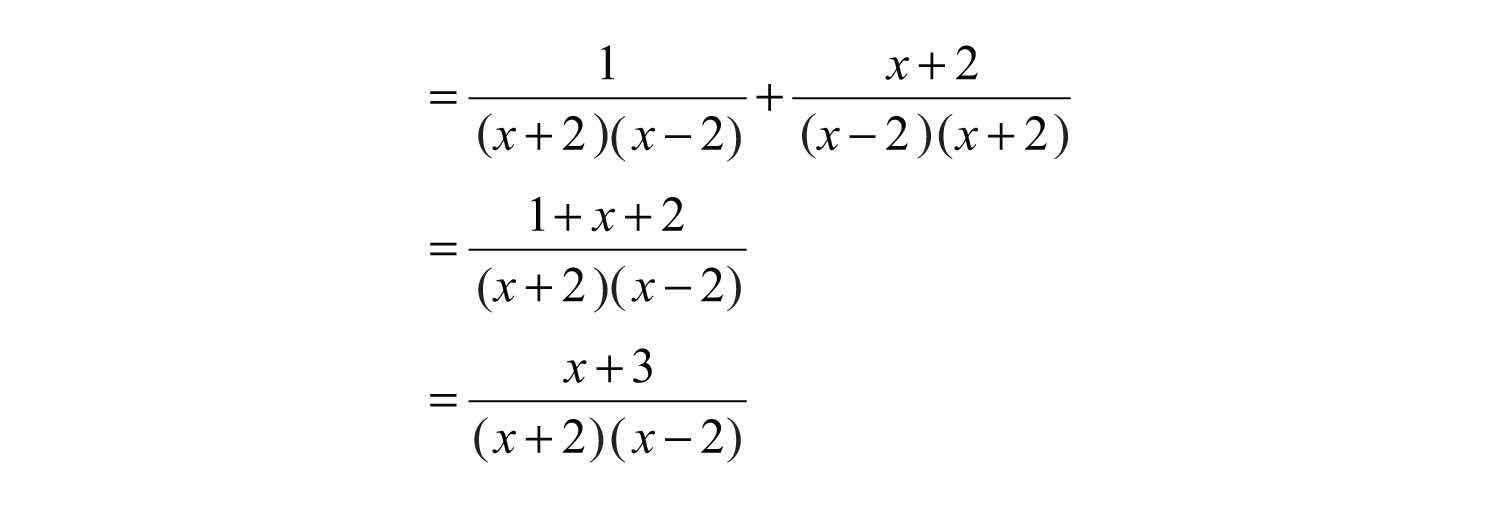
Answer:
Example 10: Simplify: .
Solution: Begin by factoring the denominator.
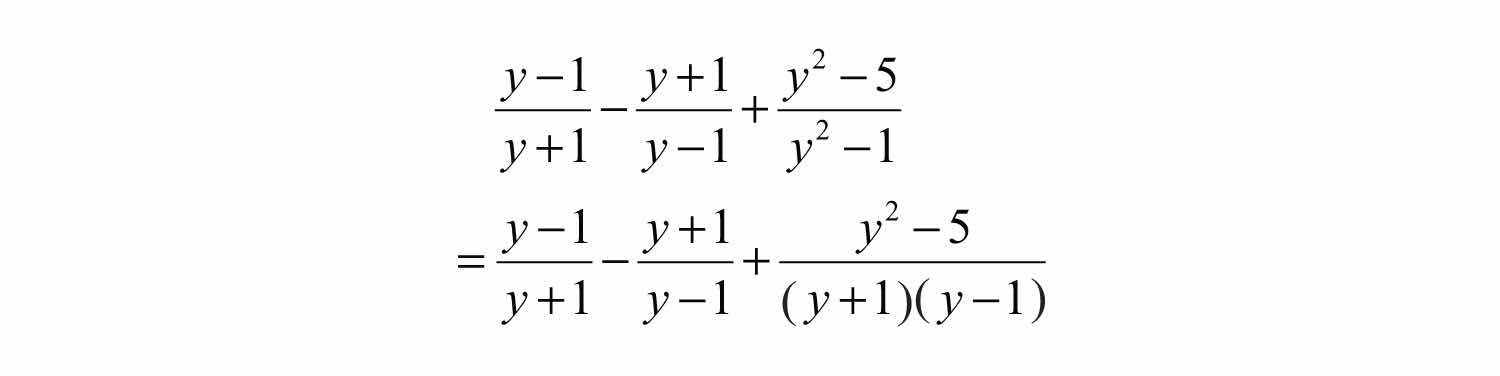
We can see that the . Find equivalent fractions with this denominator.
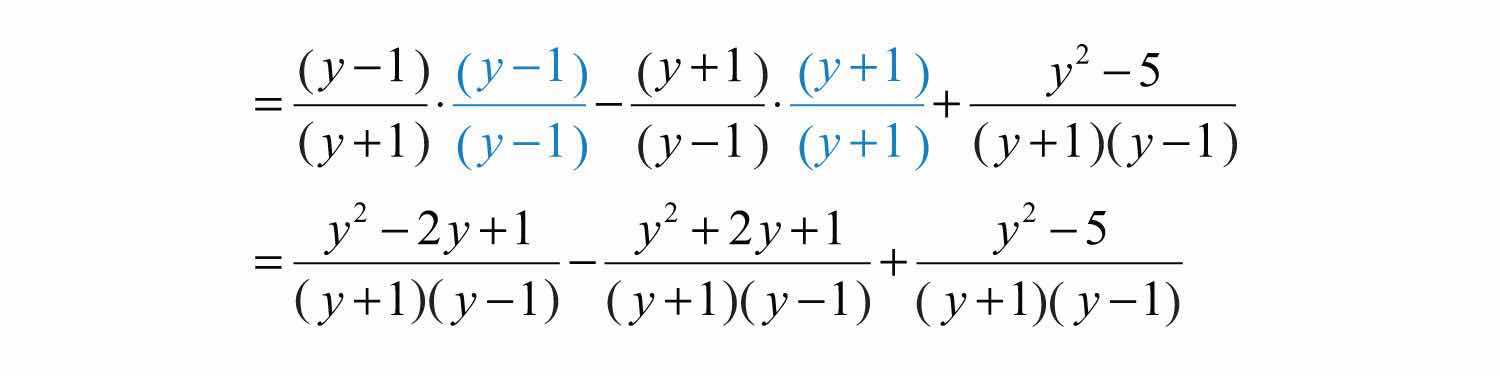
Next, subtract and add the numerators and place the result over the common denominator.
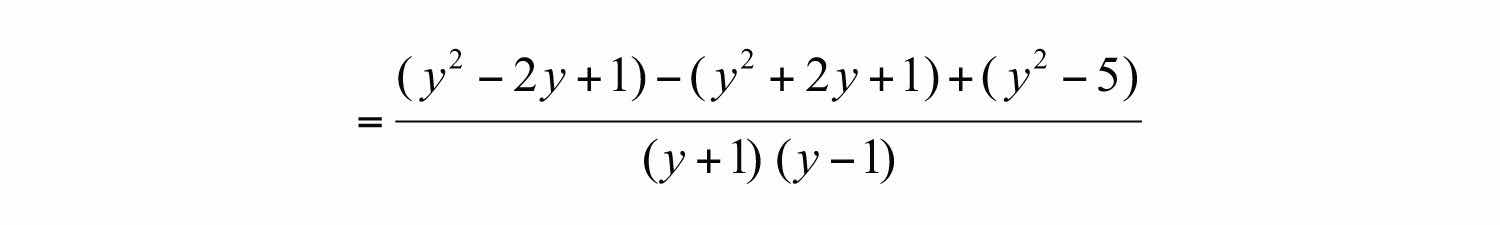
Finish by simplifying the resulting rational expression.

Answer:
Try this! Simplify: .
Answer:
Rational expressions are sometimes expressed using negative exponents. In this case, apply the rules for negative exponents before simplifying the expression.
Example 11: Simplify: .
Solution: Recall that . We begin by rewriting the negative exponents as rational expressions.

Answer:
We can simplify sums or differences of rational functions using the techniques learned in this section. The restrictions of the result consist of the restrictions to the domains of each function.
Example 12: Calculate , given and , and state the restrictions.
Solution:
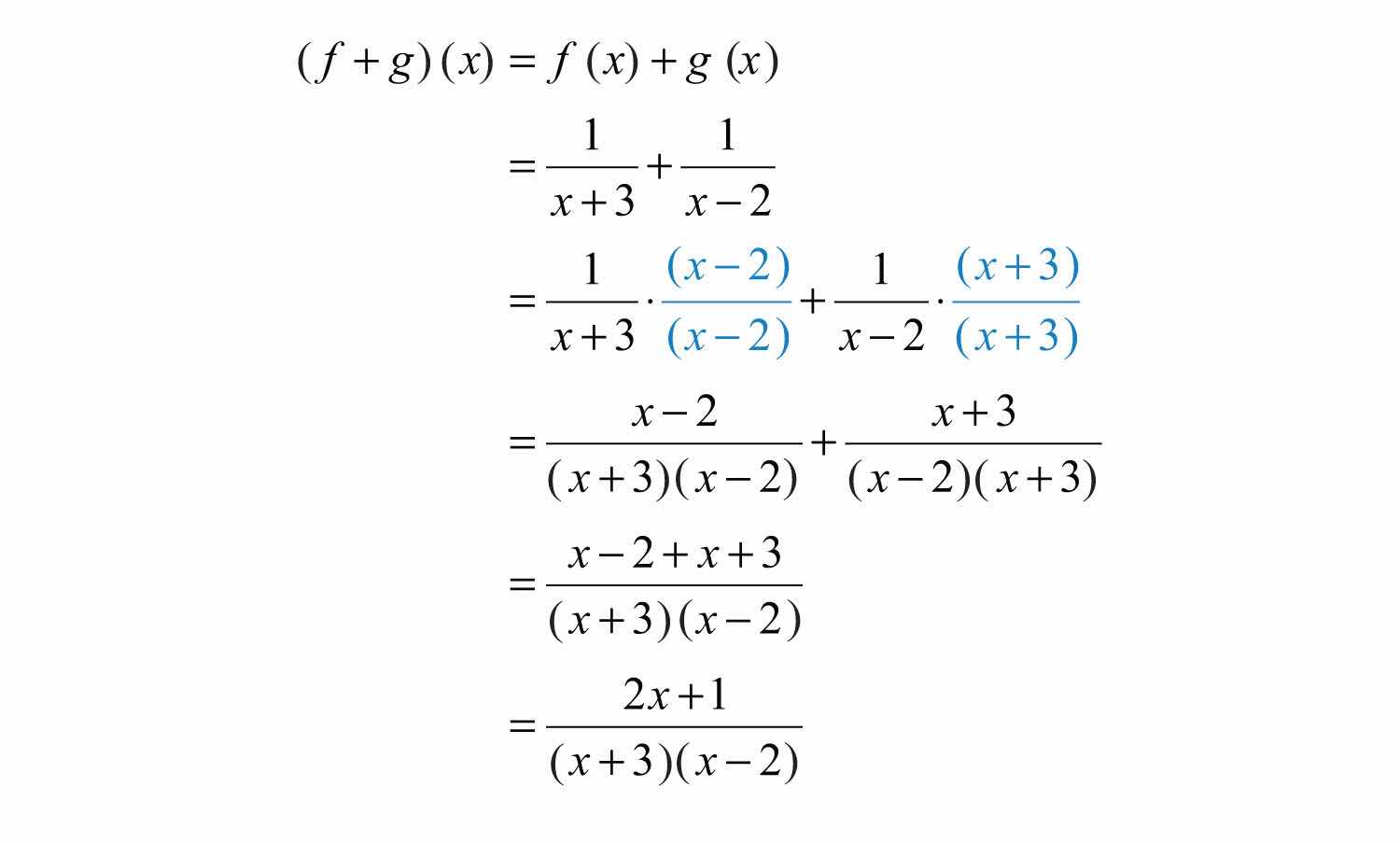
Here the domain of f consists of all real numbers except −3, and the domain of g consists of all real numbers except 2. Therefore, the domain of f + g consists of all real numbers except −3 and 2.
Answer: , where
Example 13: Calculate , given and , and state the restrictions to the domain.
Solution:
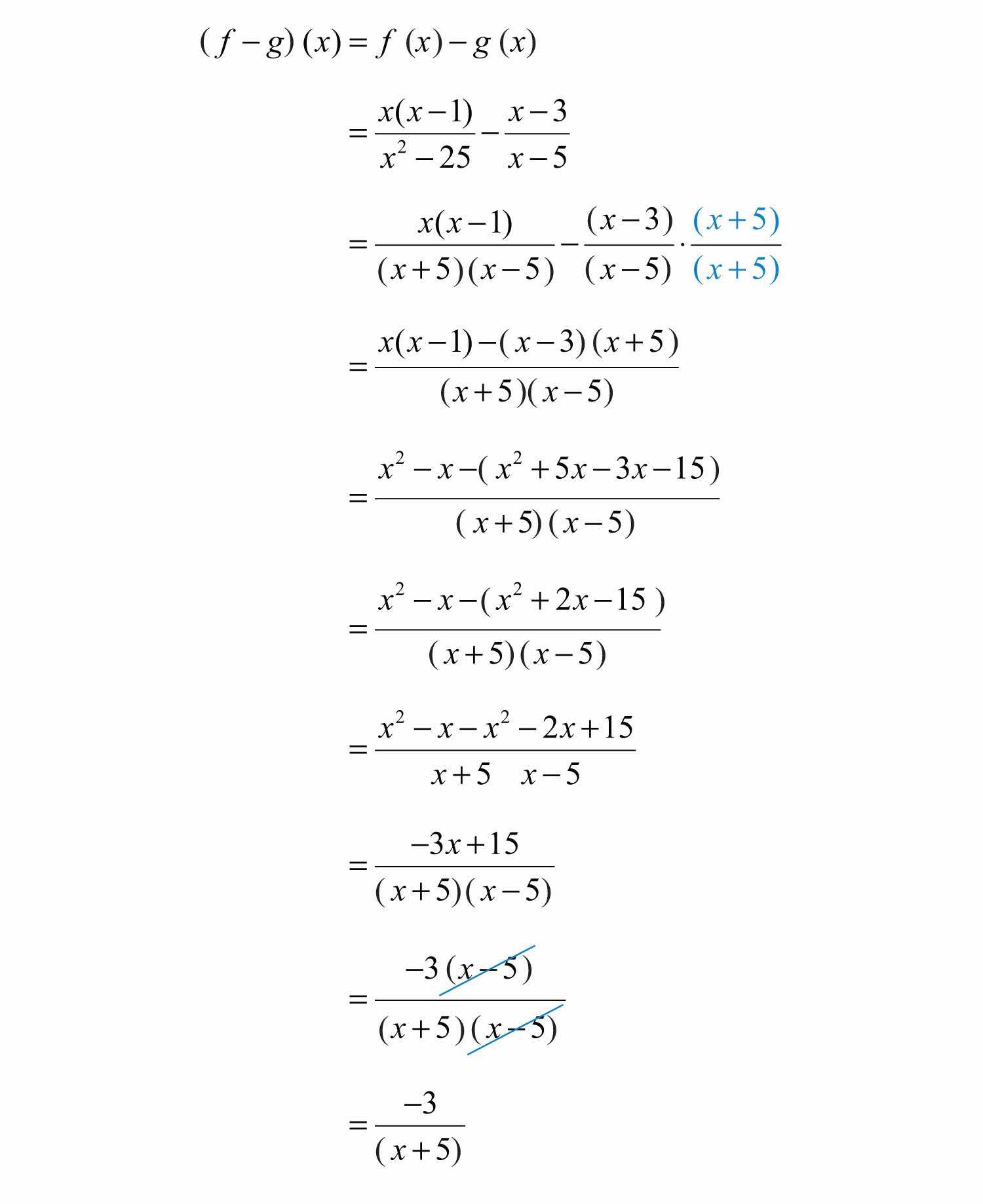
The domain of f consists of all real numbers except 5 and −5, and the domain of g consists of all real numbers except 5. Therefore, the domain of f − g consists of all real numbers except −5 and 5.
Answer: , where
Part A: Adding and Subtracting with Common Denominators
Simplify. (Assume all denominators are nonzero.)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Part B: Adding and Subtracting with Unlike Denominators
Simplify. (Assume all denominators are nonzero.)
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
Part C: Adding and Subtracting Rational Functions
Calculate and and state the restrictions to the domain.
81. and
82. and
83. and
84. and
85. and
86. and
Calculate and state the restrictions to the domain.
87.
88.
89.
90.
Part D: Discussion Board
91. Explain to a classmate why this is incorrect: .
92. Explain to a classmate how to find the common denominator when adding algebraic expressions. Give an example.
1:
3:
5:
7: 1
9:
11:
13:
15:
17:
19:
21:
23:
25:
27:
29:
31:
33:
35:
37:
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77:
79:
81: ; ;
83: ; ;
85: ; ;
87: ;
89: ;