Introduction to Polynomials

5.2 Introduction to Polynomials

Learning Objectives

Identify a polynomial and determine its degree.
Evaluate a polynomial for given values of the variables.
Evaluate a polynomial using function notation.

Definitions

A polynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. is a special algebraic expression with terms that consist of real number coefficients and variable factors with whole number exponents.

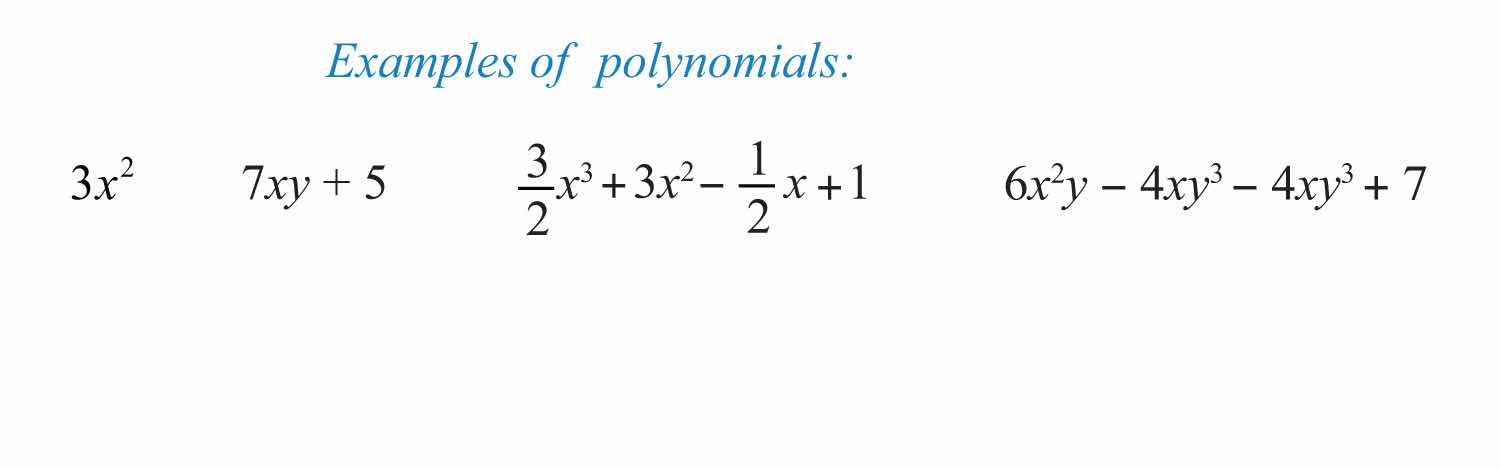
Polynomials do not have variables in the denominator of any term.

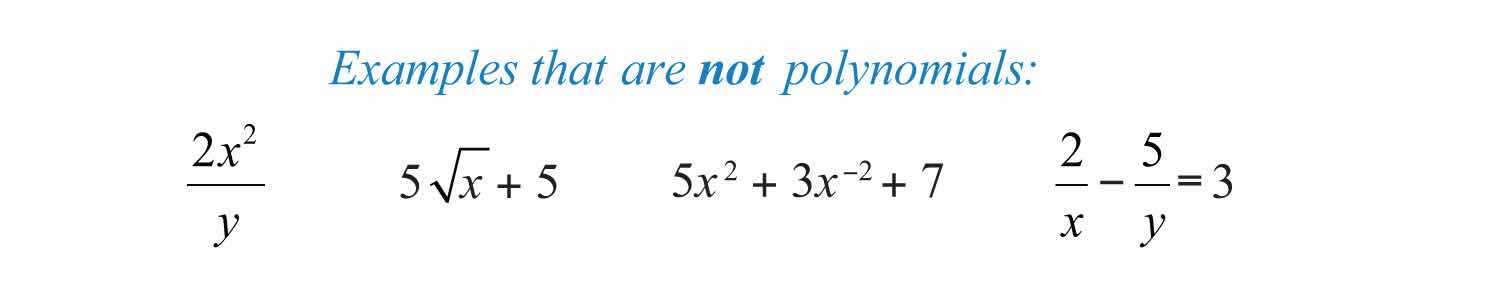
The degree of a termThe exponent of the variable; if there is more than one variable in the term, the degree of the term is the sum their exponents. in a polynomial is defined to be the exponent of the variable, or if there is more than one variable in the term, the degree is the sum of their exponents. Recall that $x^{0} = 1$ ; any constant term can be written as a product of $x^{0}$ and itself. Hence the degree of a constant term is 0.

Term	Degree
$3 x^{2}$	$2$
$6 x^{2} y$	$2 + 1 = 3$
$7 a^{2} b^{3}$	$2 + 3 = 5$
$8$	$0$ , since $8 = 8 x^{0}$
$2 x$	1, since $x = x^{1}$

The degree of a polynomialThe largest degree of all of its terms. is the largest degree of all of its terms.

Polynomial	Degree
$4 x^{5} - 3 x^{3} + 2 x - 1$	$5$
$6 x^{2} y - 5 x y^{3} + 7$	$4$ , because $5 x y^{3}$ has degree 4.
$\frac{1}{2} x + \frac{5}{4}$	1, because $x = x^{1}$

We classify polynomials by the number of terms and the degree as follows:

Expression	Classification	Degree
$5 x^{7}$	MonomialPolynomial with one term. (one term)	7
$8 x^{6} - 1$	BinomialPolynomial with two terms. (two terms)	6
$- 3 x^{2} + x - 1$	TrinomialPolynomial with three terms. (three terms)	2
$5 x^{3} - 2 x^{2} + 3 x - 6$	PolynomialAn algebraic expression consisting of terms with real number coefficients and variables with whole number exponents. (many terms)	3

In this text, we will call polynomials with four or more terms simply polynomials.

Example 1: Classify and state the degree: $7 x^{2} - 4 x^{5} - 1$ .

Solution: Here there are three terms. The highest variable exponent is 5. Therefore, this is a trinomial of degree 5.

Answer: Trinomial; degree 5

Example 2: Classify and state the degree: $12 a^{5} b c^{3}$ .

Solution: Since the expression consists of only multiplication, it is one term, a monomial. The variable part can be written as $a^{5} b^{1} c^{3}$ ; hence its degree is $5 + 1 + 3 = 9$ .

Answer: Monomial; degree 9

Example 3: Classify and state the degree: $4 x^{2} y - 6 x y^{4} + 5 x^{3} y^{3} + 4$ .

Solution: The term $4 x^{2} y$ has degree 3; $- 6 x y^{4}$ has degree 5; $5 x^{3} y^{3}$ has degree 6; and the constant term 4 has degree 0. Therefore, the polynomial has 4 terms with degree 6.

Answer: Polynomial; degree 6

Of particular interest are polynomials with one variableA polynomial where each term has the form $a_{n} x^{n}$ , where $a_{n}$ is any real number and n is any whole number., where each term is of the form $a_{n} x^{n}$ . Here $a_{n}$ is any real number and n is any whole number. Such polynomials have the standard form

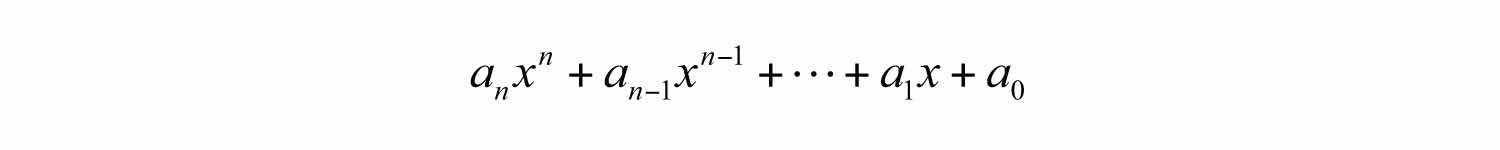
Typically, we arrange terms of polynomials in descending order based on the degree of each term. The leading coefficientThe coefficient of the term with the largest degree. is the coefficient of the variable with the highest power, in this case, $a_{n}$ .

Example 4: Write in standard form: $3 x - 4 x^{2} + 5 x^{3} + 7 - 2 x^{4}$ .

Solution: Since terms are separated by addition, write the following:

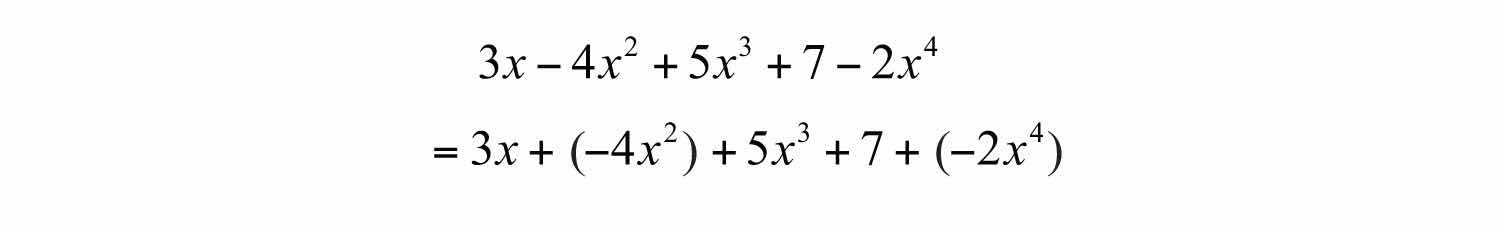
In this form, we can see that the subtraction in the original corresponds to negative coefficients. Because addition is commutative, we can write the terms in descending order based on the degree of each term as follows:

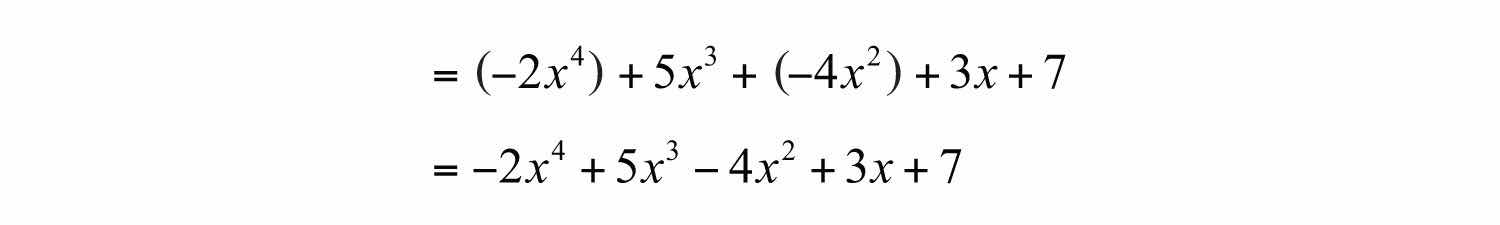
Answer: $- 2 x^{4} + 5 x^{3} - 4 x^{2} + 3 x + 7$

We can further classify polynomials with one variable by their degree as follows:

Polynomial	Name
5	Constant (degree 0)
$2 x + 1$	Linear (degree 1)
$3 x^{2} + 5 x - 3$	Quadratic (degree 2)
$x^{3} + x^{2} + x + 1$	Cubic (degree 3)
$7 x^{4} + 3 x^{3} - 7 x + 8$	Fourth-degree polynomial

In this text, we call any polynomial of degree $n \geq 4$ an nth-degree polynomial. In other words, if the degree is 4, we call the polynomial a fourth-degree polynomial. If the degree is 5, we call it a fifth-degree polynomial, and so on.

Evaluating Polynomials

Given the values for the variables in a polynomial, we can substitute and simplify using the order of operations.

Example 5: Evaluate: $3 x - 1$ , where $x = - \frac{3}{2}$ .

Solution: First, replace the variable with parentheses and then substitute the given value.

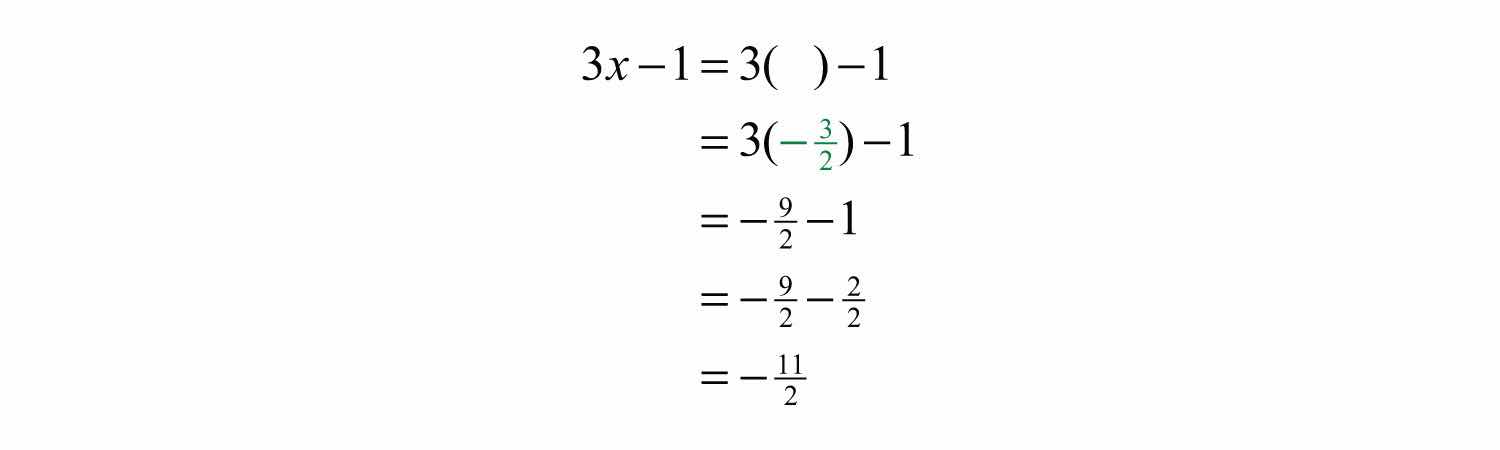
Answer: −11/2

Example 6: Evaluate: $3 x^{2} + 2 x - 1$ , where $x = - 1$ .

Solution:

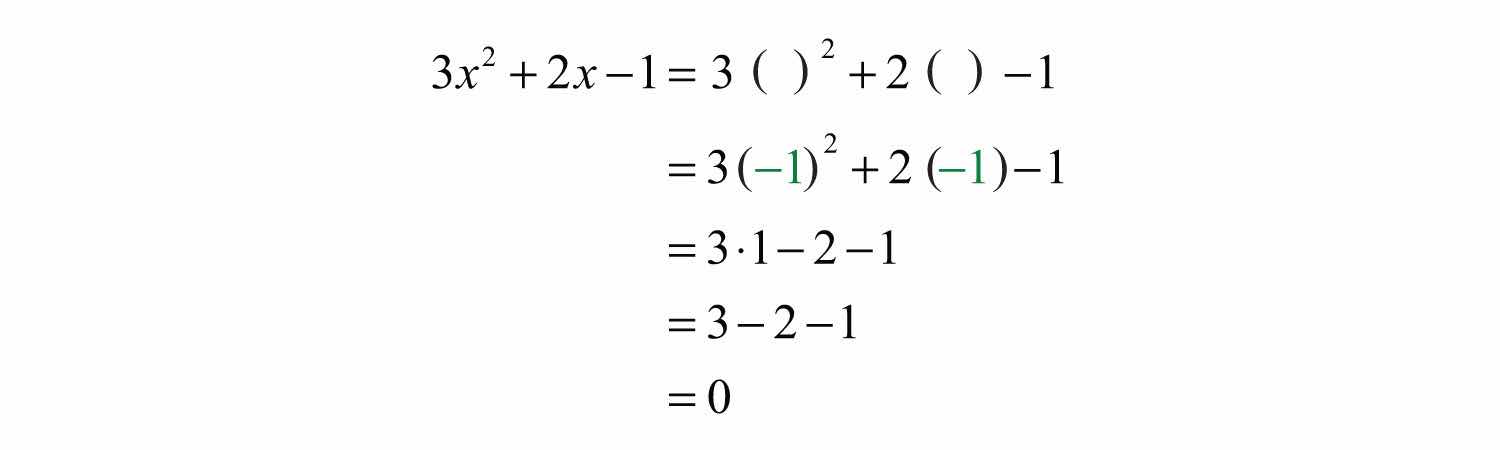
Answer: 0

Example 7: Evaluate: $- 2 a^{2} b + a b^{2} - 7$ , where $a = 3$ and $b = - 2$ .

Solution:

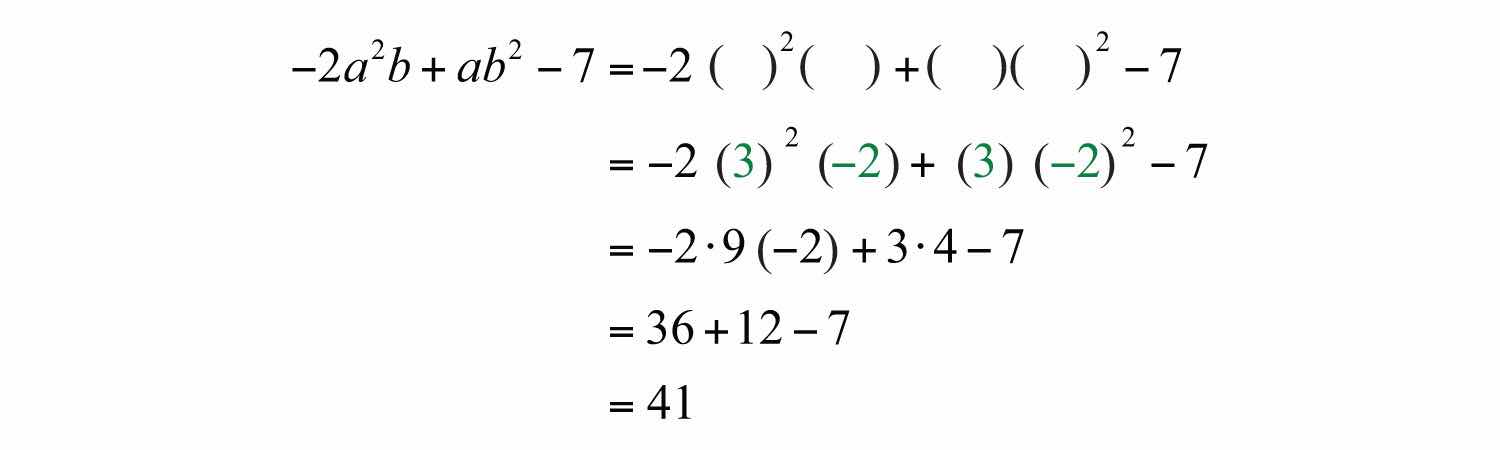
Answer: 41

Example 8: The volume of a sphere in cubic units is given by the formula $V = \frac{4}{3} π r^{3}$ , where r is the radius. Calculate the volume of a sphere with radius $r = \frac{3}{2}$ meters.

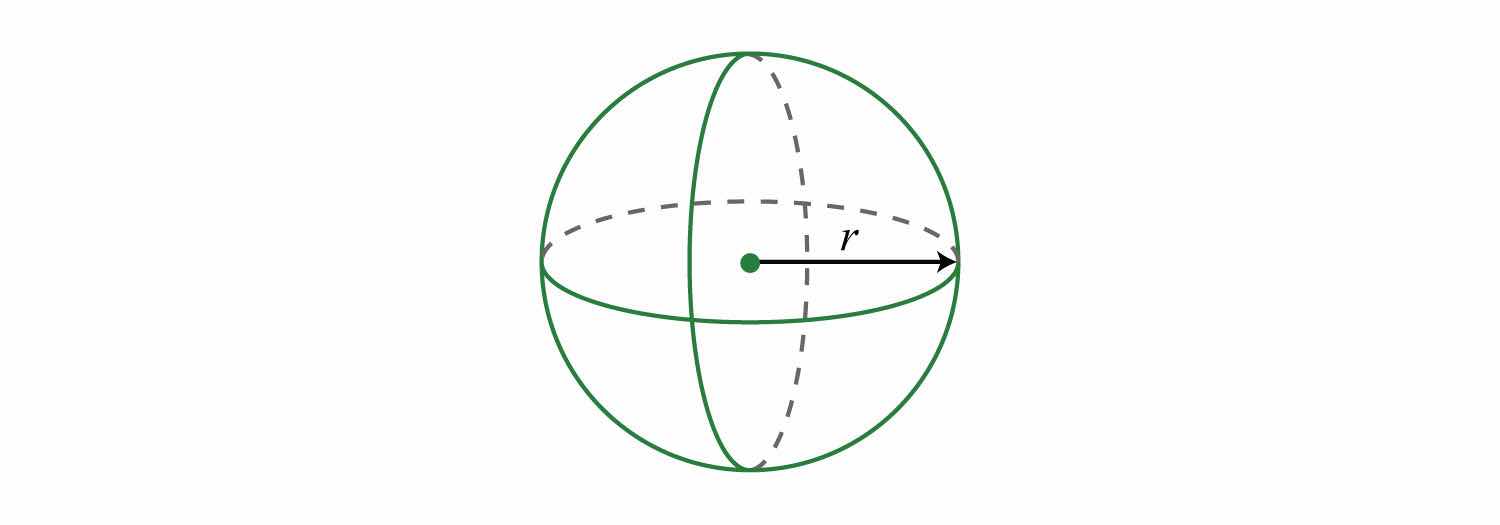
Solution:

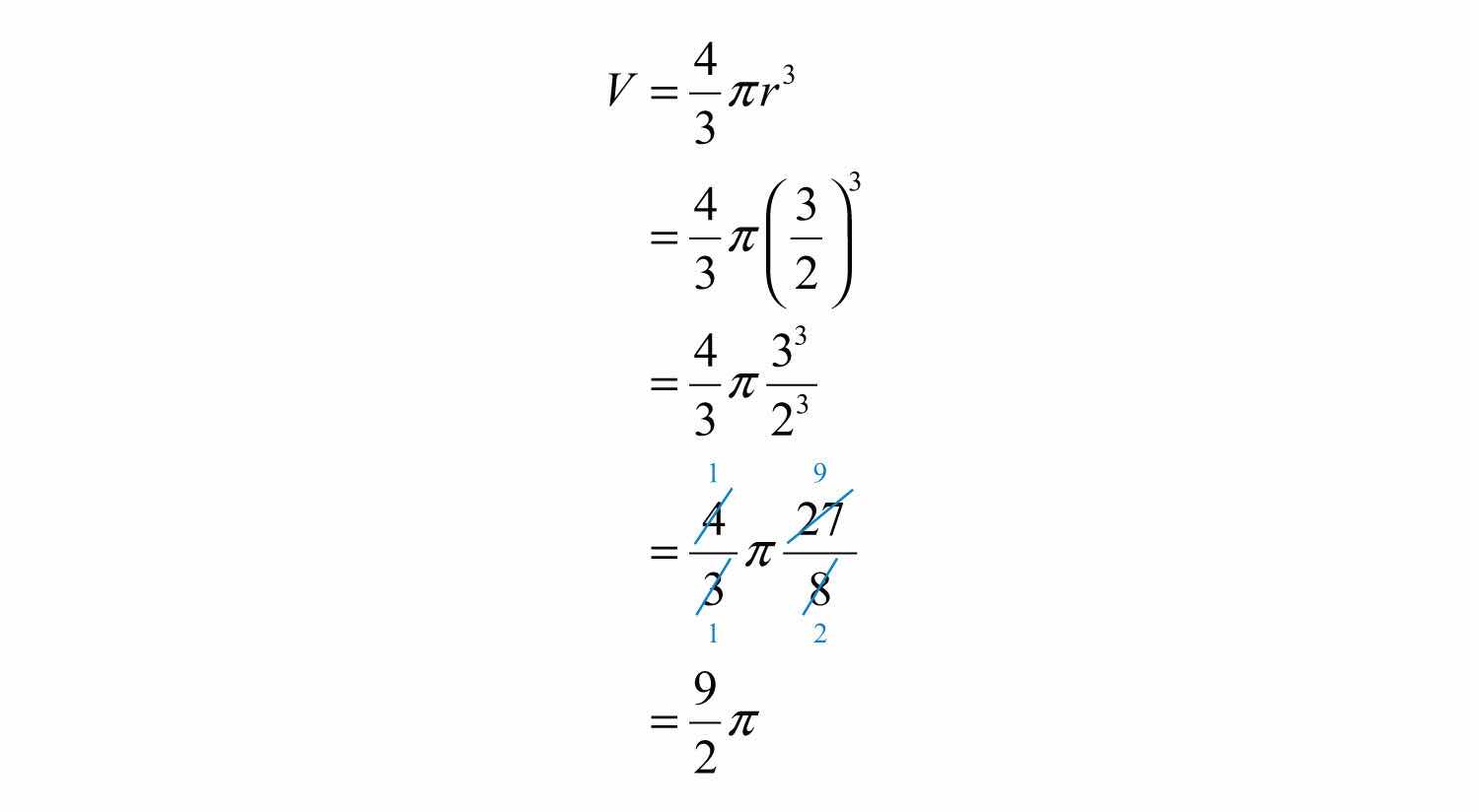
Answer: $\frac{9}{2} π$ cubic meters

Try this! Evaluate: $x^{3} - x^{2} + 4 x - 2$ , where $x = - 3$ .

Answer: −50

Video Solution

(click to see video)

Polynomial Functions

Polynomial functions with one variable are functions that can be written in the form

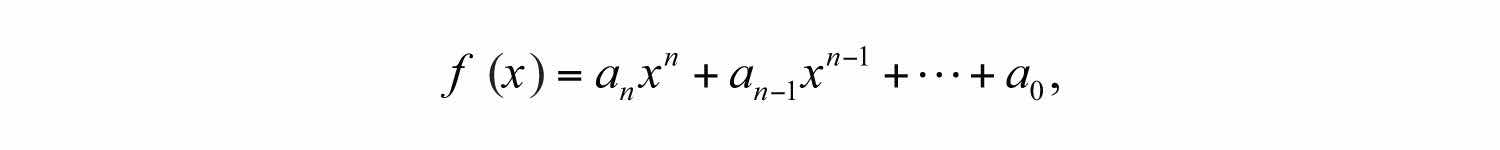
where $a_{n}$ is any real number and n is any whole number. Some examples of the different classes of polynomial functions are listed below:

Polynomial function	Name
$f (x) = 5$	Constant functionA polynomial function with degree 0. (degree 0)
$f (x) = - 2 x + 1$	Linear functionA polynomial function with degree 1. (degree 1)
$f (x) = 5 x^{2} + 4 x - 3$	Quadratic functionA polynomial function with degree 2. (degree 2)
$f (x) = x^{3} - 1$	Cubic functionA polynomial function with degree 3. (degree 3)
$f (x) = 4 x^{5} + 3 x^{4} - 7$	Polynomial function

Since there are no restrictions on the values for x, the domain of any polynomial function consists of all real numbers.

Example 9: Calculate: $f (5)$ , given $f (x) = - 2 x^{2} + 5 x + 10$ .

Solution: Recall that the function notation $f (5)$ indicates we should evaluate the function when $x = 5$ . Replace every instance of the variable x with the value 5.

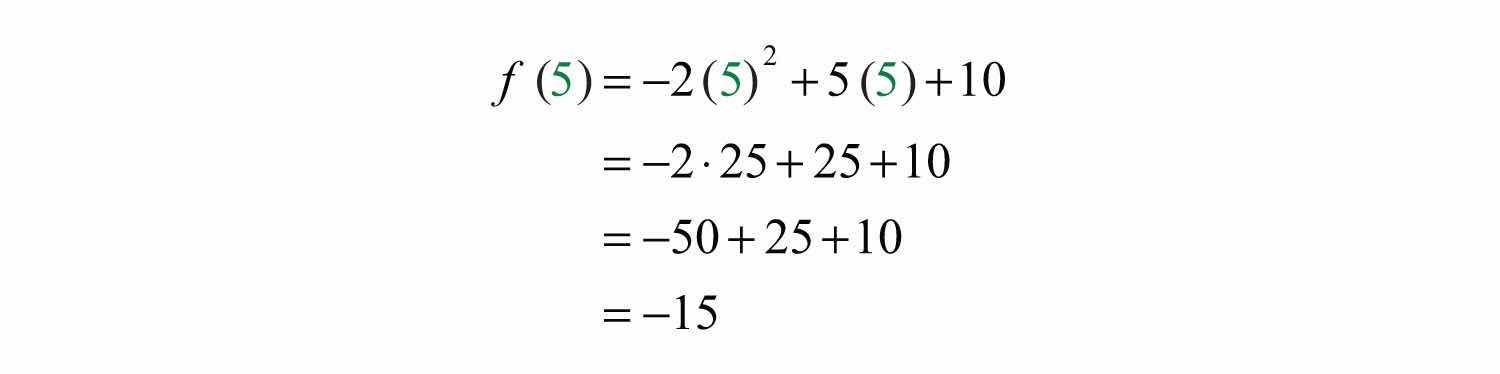
Answer: $f (5) = - 15$

Example 10: Calculate: $f (- 1)$ , given $f (x) = - x^{3} + 2 x^{2} - 4 x + 1$ .

Solution: Replace the variable x with −1.

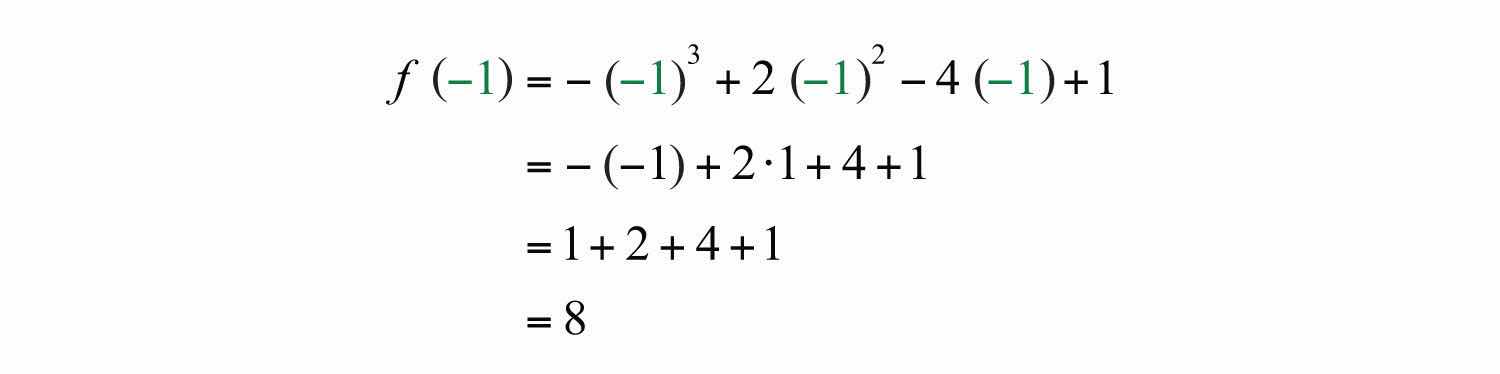
Answer: $f (- 1) = 8$

Try this! Given $g (x) = x^{3} - 2 x^{2} - x - 4$ , calculate $g (- 1)$ .

Answer: $g (- 1) = - 6$

Video Solution

(click to see video)

Key Takeaways

Polynomials are special algebraic expressions where the terms are the products of real numbers and variables with whole number exponents.
The degree of a polynomial with one variable is the largest exponent of the variable found in any term.
The terms of a polynomial are typically arranged in descending order based on the degree of each term.
When evaluating a polynomial, it is a good practice to replace all variables with parentheses and then substitute the appropriate values.
All polynomials are functions.

Topic Exercises

Part A: Definitions

Classify the given polynomial as linear, quadratic, or cubic.

1. $2 x + 1$

2. $x^{2} + 7 x + 2$

3. $2 - 3 x^{2} + x$

4. $4 x$

5. $x^{2} - x^{3} + x + 1$

6. $5 - 10 x^{3}$

Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.

7. $x^{3} - 1$

8. $x^{2} y^{2}$

9. $x - x^{5} + 1$

10. $x^{2} + 3 x - 1$

11. $5 a b^{4}$

12. $\frac{1}{3} x - \frac{1}{2}$

13. $- 5 x^{3} + 2 x + 1$

14. $8 x^{2} - 9$

15. $4 x^{5} - 5 x^{3} + 6 x$

16. $8 x^{4} - x^{5} + 2 x - 3$

17. $9 x + 7$

18. $x^{5} + x^{4} + x^{3} + x^{2} - x + 1$

19. $6 x^{- 1} + 5 x^{4} - 8$

20. $\frac{4}{x} - 3 x^{2} + 3$

21. $7$

22. $x^{2}$

23. $4 x^{2} y - 3 x^{3} y^{3} + x y^{3}$

24. $a^{3} b^{2} - 6 a b$

25. $a^{3} b^{3}$

26. $\frac{x^{2}}{y} - \frac{y^{2}}{x}$

27. $x y - 3$

28. $a^{5} b c^{2} + 3 a^{9} - 5 a^{4} b^{3} c$

29. $- 3 x^{10} y^{2} z - x y^{12} z + 9 x^{13} + 30$

30. $7 x^{0}$

Write the following polynomials in standard form.

31. $1 - 6 x + 7 x^{2}$

32. $x - 9 x^{2} - 8$

33. $7 - x^{3} + x^{7} - x^{2} + x - 5 x^{5}$

34. $a^{3} - a^{9} + 6 a^{5} - a + 3 - a^{4}$

Part B: Evaluating Polynomials

35. Fill in the following chart:

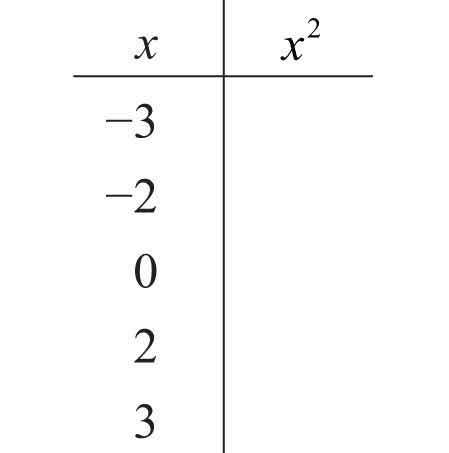
36. Fill in the following chart:

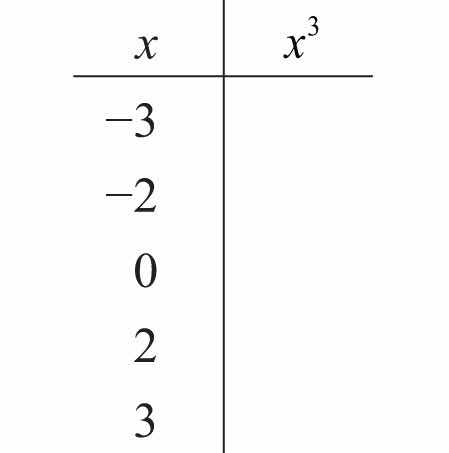
Evaluate.

37. $2 x - 3$ , where $x = 3$

38. $x^{2} - 3 x + 5$ , where $x = - 2$

39. $- \frac{1}{2} x + \frac{1}{3}$ , where $x = - \frac{1}{3}$

40. $- x^{2} + 5 x - 1$ , where $x = - \frac{1}{2}$

41. $- 2 x^{2} + 3 x - 5$ , where $x = 0$

42. $8 x^{5} - 27 x^{3} + 81 x - 17$ , where $x = 0$

43. $y^{3} - 2 y + 1$ , where $y = - 2$

44. $y^{4} + 2 y^{2} - 32$ , where $y = 2$

45. $a^{3} + 2 a^{2} + a - 3$ , where $a = - 3$

46. $x^{3} - x^{2}$ , where $x = 5$

47. $\frac{3}{4} x^{2} - \frac{1}{2} x + \frac{3}{6}$ , where $x = - \frac{2}{3}$

48. $\frac{5}{8} x^{2} - \frac{1}{4} x + \frac{1}{2}$ , where $x = 4$

49. $x^{2} y + x y^{2}$ , where $x = 2$ and $y = - 3$

50. $2 a^{5} b - a b^{4} + a^{2} b^{2}$ , where $a = - 1$ and $b = - 2$

51. $a^{2} - b^{2}$ , where $a = 5$ and $b = - 6$

52. $a^{2} - b^{2}$ , where $a = \frac{3}{4}$ and $b = - \frac{1}{4}$

53. $a^{3} - b^{3}$ , where $a = - 2$ and $b = 3$

54. $a^{3} + b^{3}$ , where $a = 5$ and $b = - 5$

For each problem, evaluate $b^{2} - 4 a c$ , given the following values.

55. $a = - 1$ , $b = 2$ , and $c = - 1$

56. $a = 2$ , $b = - 2$ , and $c = \frac{1}{2}$

57. $a = 3$ , $b = - 5$ , $c = 0$

58. $a = 1$ , $b = 0$ , and $c = - 4$

59. $a = \frac{1}{4}$ , $b = - 4$ , and $c = 2$

60. $a = 1$ , $b = 5$ , and $c = 6$

The volume of a sphere in cubic units is given by the formula $V = \frac{4}{3} π r^{3}$ , where r is the radius. For each problem, calculate the volume of a sphere given the following radii.

61. r = 3 centimeters

62. r = 1 centimeter

63. r = 1/2 feet

64. r = 3/2 feet

65. r = 0.15 in

66. r = 1.3 inches

The height in feet of a projectile launched vertically from the ground with an initial velocity $v_{0}$ in feet per second is given by the formula $h = - 16 t^{2} + v_{0} t$ , where t represents time in seconds. For each problem, calculate the height of the projectile given the following initial velocity and times.

67. $v_{0} = 64 feet/second$ , at times t = 0, 1, 2, 3, 4 seconds

68. $v_{0} = 80 feet/second$ , at times t = 0, 1, 2, 2.5, 3, 4, 5 seconds

The stopping distance of a car, taking into account an average reaction time, can be estimated with the formula $d = 0.05 v^{2} + 1.5$ , where d is in feet and v is the speed in miles per hour. For each problem, calculate the stopping distance of a car traveling at the given speeds.

69. 20 miles per hour

70. 40 miles per hour

71. 80 miles per hour

72. 100 miles per hour

Part C: Polynomial Functions

Given the linear function $f (x) = \frac{2}{3} x + 6$ , evaluate each of the following.

73. $f (- 6)$

74. $f (- 3)$

75. $f (0)$

76. $f (3)$

77. Find x when $f (x) = 10$ .

78. Find x when $f (x) = - 4$ .

Given the quadratic function $f (x) = 2 x^{2} - 3 x + 5$ , evaluate each of the following.

79. $f (- 2)$

80. $f (- 1)$

81. $f (0)$

82. $f (2)$

Given the cubic function $g (x) = x^{3} - x^{2} + x - 1$ , evaluate each of the following.

83. $g (- 2)$

84. $g (- 1)$

85. $g (0)$

86. $g (1)$

The height in feet of a projectile launched vertically from the ground with an initial velocity of 128 feet per second is given by the function $h (t) = - 16 t^{2} + 128 t$ , where t is in seconds. Calculate and interpret the following.

87. $h (0)$

88. $h (\frac{1}{2})$

89. $h (1)$

90. $h (3)$

91. $h (4)$

92. $h (5)$

93. $h (7)$

94. $h (8)$

Part D: Discussion Board Topics

95. Find and share some graphs of polynomial functions.

96. Explain how to convert feet per second into miles per hour.

97. Find and share the names of fourth-degree, fifth-degree, and higher polynomials.

Answers

1: Linear

3: Quadratic

5: Cubic

7: Binomial; degree 3

9: Trinomial; degree 5

11: Monomial; degree 5

13: Trinomial; degree 3

15: Trinomial; degree 5

17: Binomial; degree 1

19: Not a polynomial

21: Monomial; degree 0

23: Trinomial; degree 6

25: Monomial; degree 6

27: Binomial; degree 2

29: Polynomial; degree 14

31: $7 x^{2} - 6 x + 1$

33: $x^{7} - 5 x^{5} - x^{3} - x^{2} + x + 7$

35:

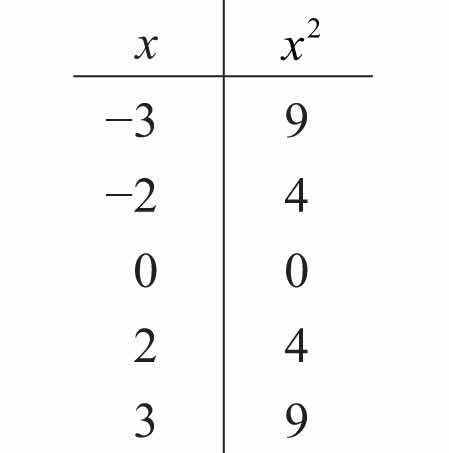
37: 3

39: 1/2

41: −5

43: −3

45: −15

47: 7/6

49: 6

51: −11

53: −35

55: 0

57: 25

59: 14

61: 36π cubic centimeters

63: π/6 cubic feet

65: 0.014 cubic inches

67:

Time	Height
t = 0 seconds	h = 0 feet
t = 1 second	h = 48 feet
t = 2 seconds	h = 64 feet
t = 3 seconds	h = 48 feet
t = 4 seconds	h = 0 feet

69: 21.5 feet

71: 321.5 feet

73: 2

75: 6

77: $x = 6$

79: 19

81: 5

83: −15

85: −1

87: The projectile is launched from the ground.

89: The projectile is 112 feet above the ground 1 second after launch.

91: The projectile is 256 feet above the ground 4 seconds after launch.

93: The projectile is 112 feet above the ground 7 seconds after launch.