Order of Operations

1.7 Order of Operations

Learning Objectives

Identify and work with grouping symbols.
Understand the order of operations.
Simplify using the order of operations.

Grouping Symbols

In a computation where more than one operation is involved, grouping symbols help tell us which operations to perform first. The grouping symbolsParentheses, brackets, braces, and the fraction bar are the common symbols used to group expressions and mathematical operations within a computation. commonly used in algebra are

All of the above grouping symbols, as well as absolute value, have the same order of precedence. Perform operations inside the innermost grouping symbol or absolute value first.

Example 1: Simplify: $5 - (4 - 12)$ .

Solution: Perform the operations within the parentheses first. In this case, first subtract 12 from 4.

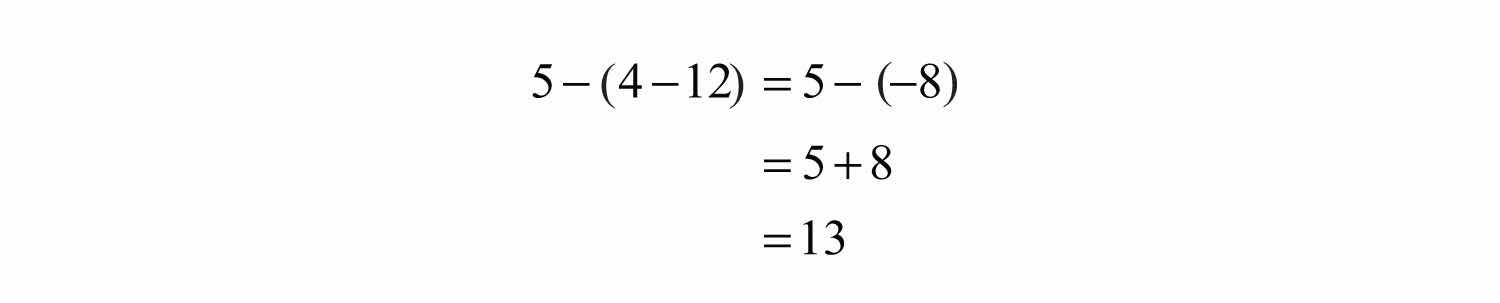
Answer: 13

Example 2: Simplify: $3 {- 2 [- (- 3 - 1)]}$ .

Solution:

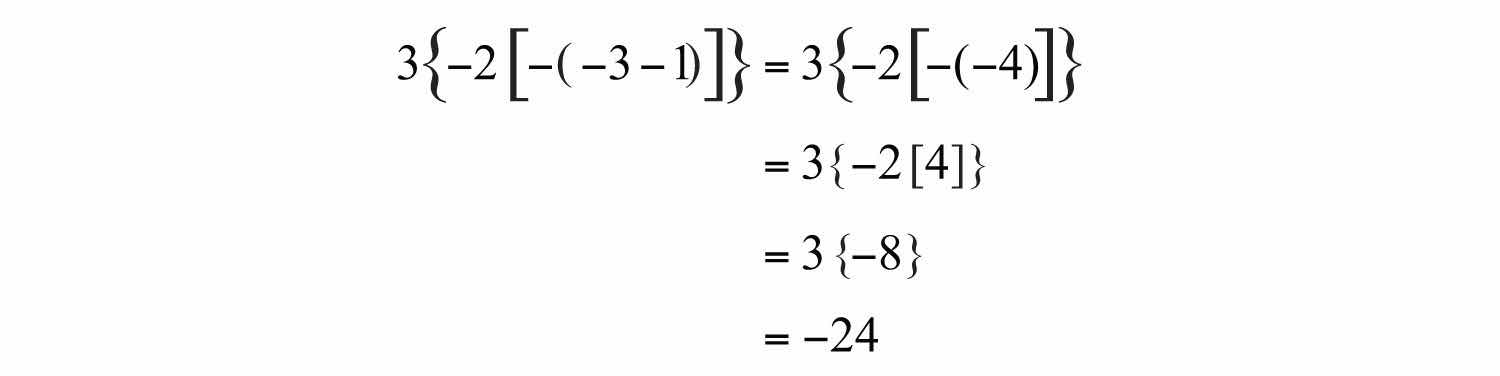
Answer: −24

Example 3: Simplify: $\frac{5 - | 4 - (- 3) |}{| - 3 | - (5 - 7)}$ .

Solution: The fraction bar groups the numerator and denominator. They should be simplified separately.

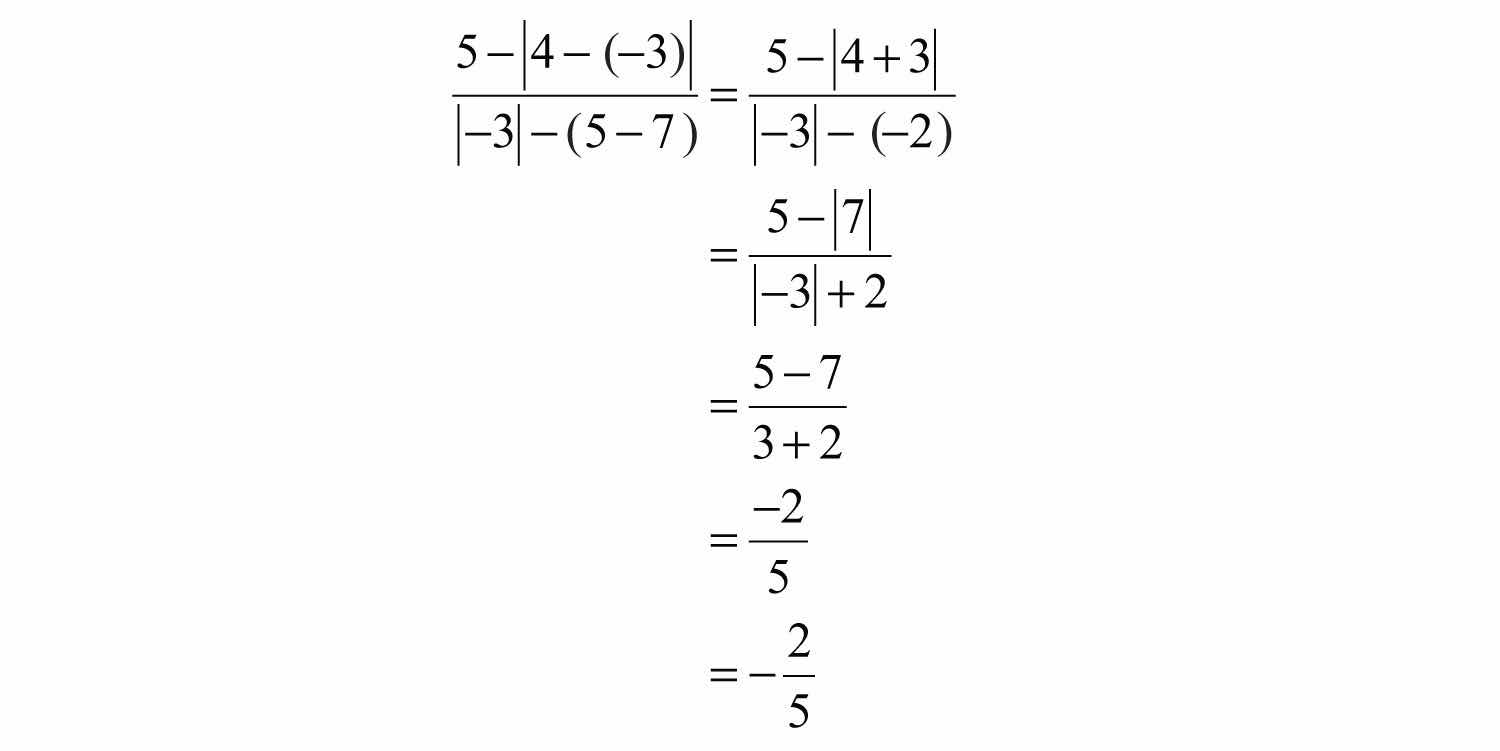
Answer: $- \frac{2}{5}$

Try this! Simplify: $- [- 3 (2 + 3)]$ .

Answer: 15

Video Solution

(click to see video)

Order of Operations

When several operations are to be applied within a calculation, we must follow a specific orderTo ensure a single correct result, perform mathematical operations in a specific order. to ensure a single correct result.

Perform all calculations within the innermost parentheses or grouping symbols.
Evaluate all exponents.
Perform multiplication and division operations from left to right.
Finally, perform all remaining addition and subtraction operations from left to right.

Caution: Note that multiplication and division operations must be worked from left to right.

Example 4: Simplify: $5^{2} - 4 \cdot 3 \div 12$ .

Solution: First, evaluate $5^{2}$ and then perform multiplication and division as they appear from left to right.

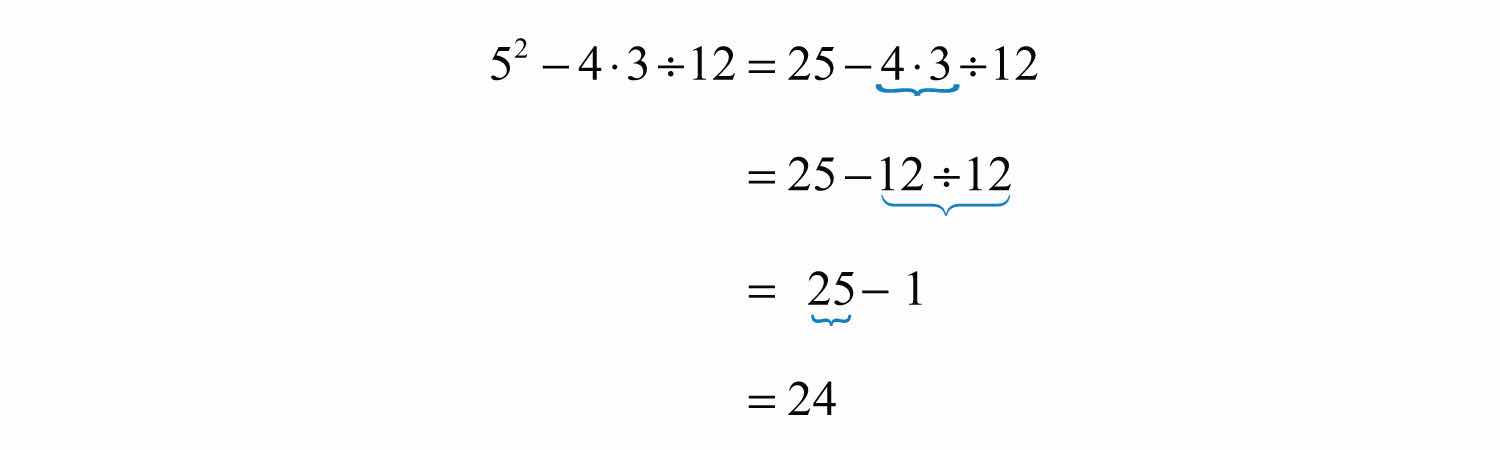
Answer: 24

Because multiplication and division operations should be worked from left to right, it is sometimes correct to perform division before multiplication.

Example 5: Simplify: $2^{4} - 12 \div 3 \cdot 2 + 11$ .

Solution: Begin by evaluating the exponent, $2^{4} = 2 \cdot 2 \cdot 2 \cdot 2 = 16$ .

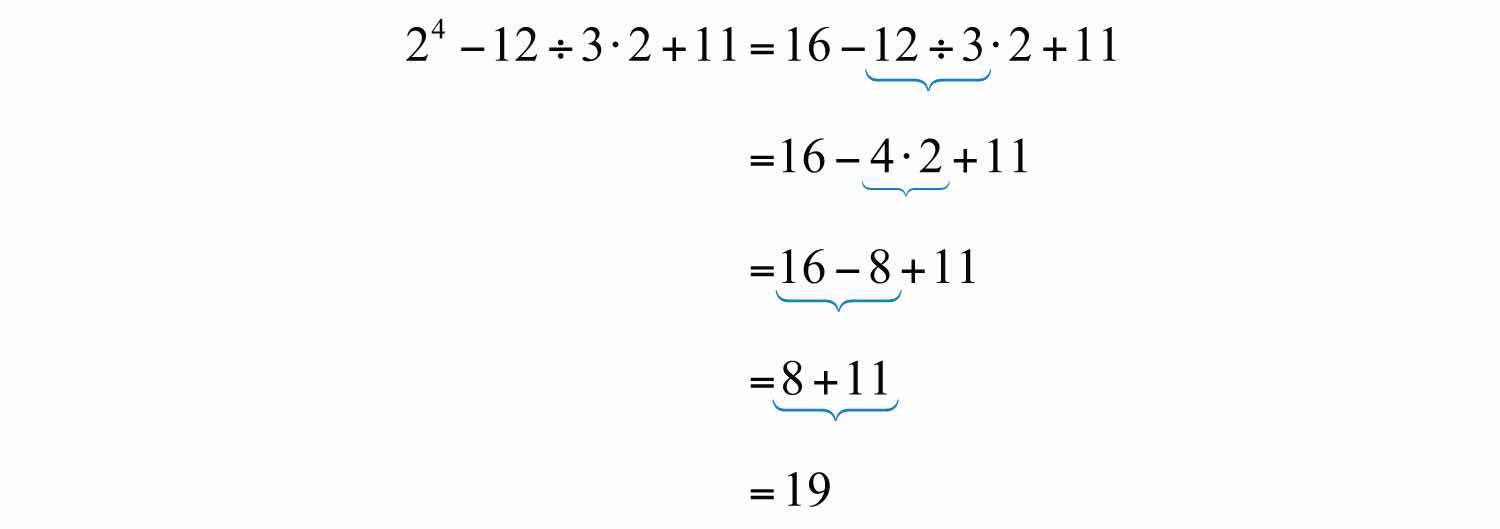
Multiplying first leads to an incorrect result.

Answer: 19

Example 6: Simplify: $- 3 - 5^{2} + {(- 7)}^{2}$ .

Solution: Take care to correctly identify the base when squaring.

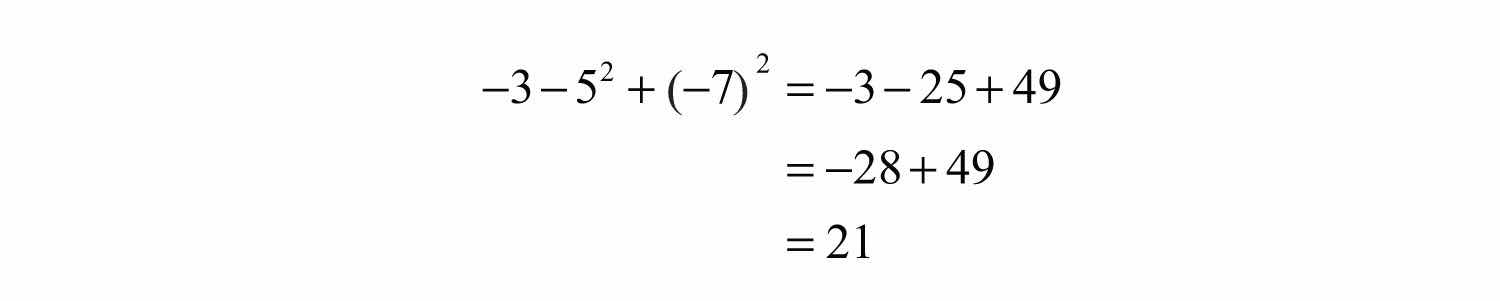
Answer: 21

Example 7: Simplify: $5 - 3 [2^{3} - 5 + 7 (- 3)]$ .

Solution: It is tempting to first subtract 5 − 3, but this will lead to an incorrect result. The order of operations requires us to simplify within the brackets first.

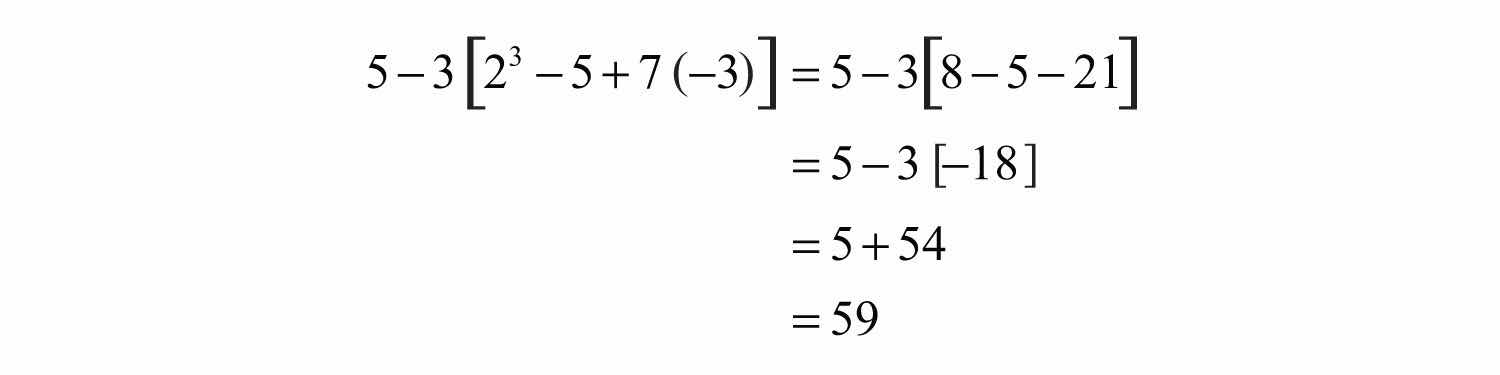
Subtracting 5 − 3 first leads to an incorrect result.

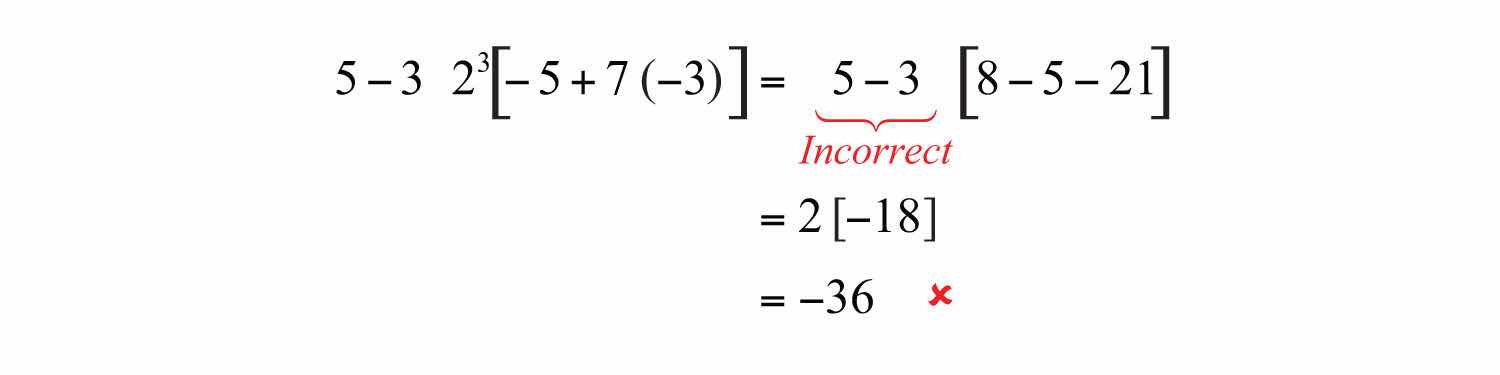
Answer: 59

Example 8: Simplify: $- 3^{2} - [5 - (4^{2} - 10)]$ .

Solution: Perform the operations within the innermost parentheses first.

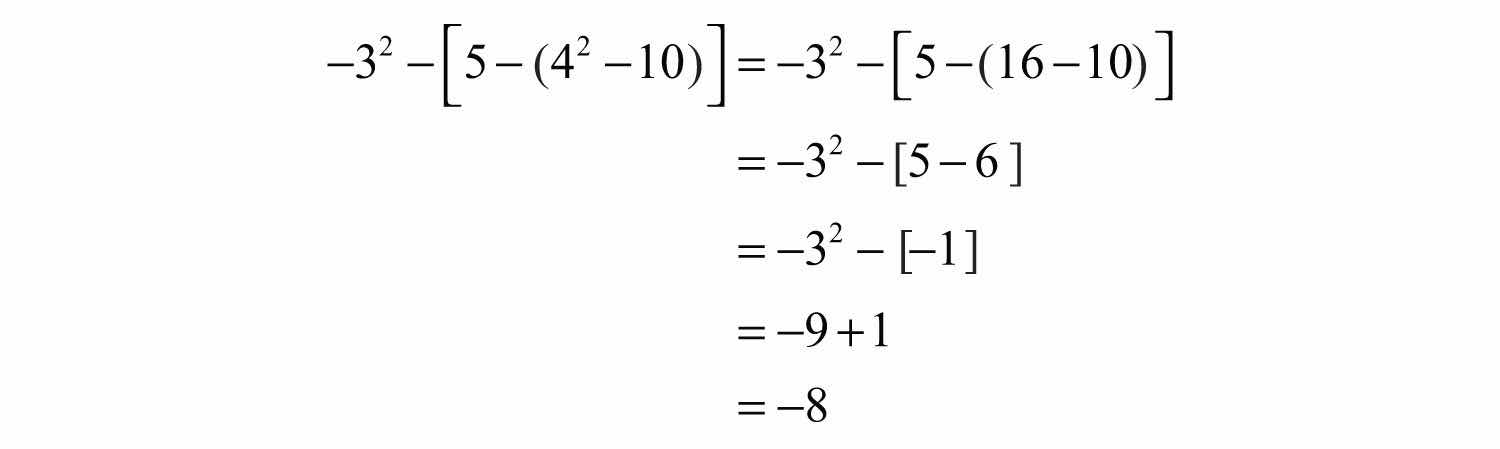
Answer: −8

Example 9: Simplify: ${(- \frac{2}{3})}^{2} \div [\frac{5}{3} - {(- \frac{1}{2})}^{3}]$ .

Solution:

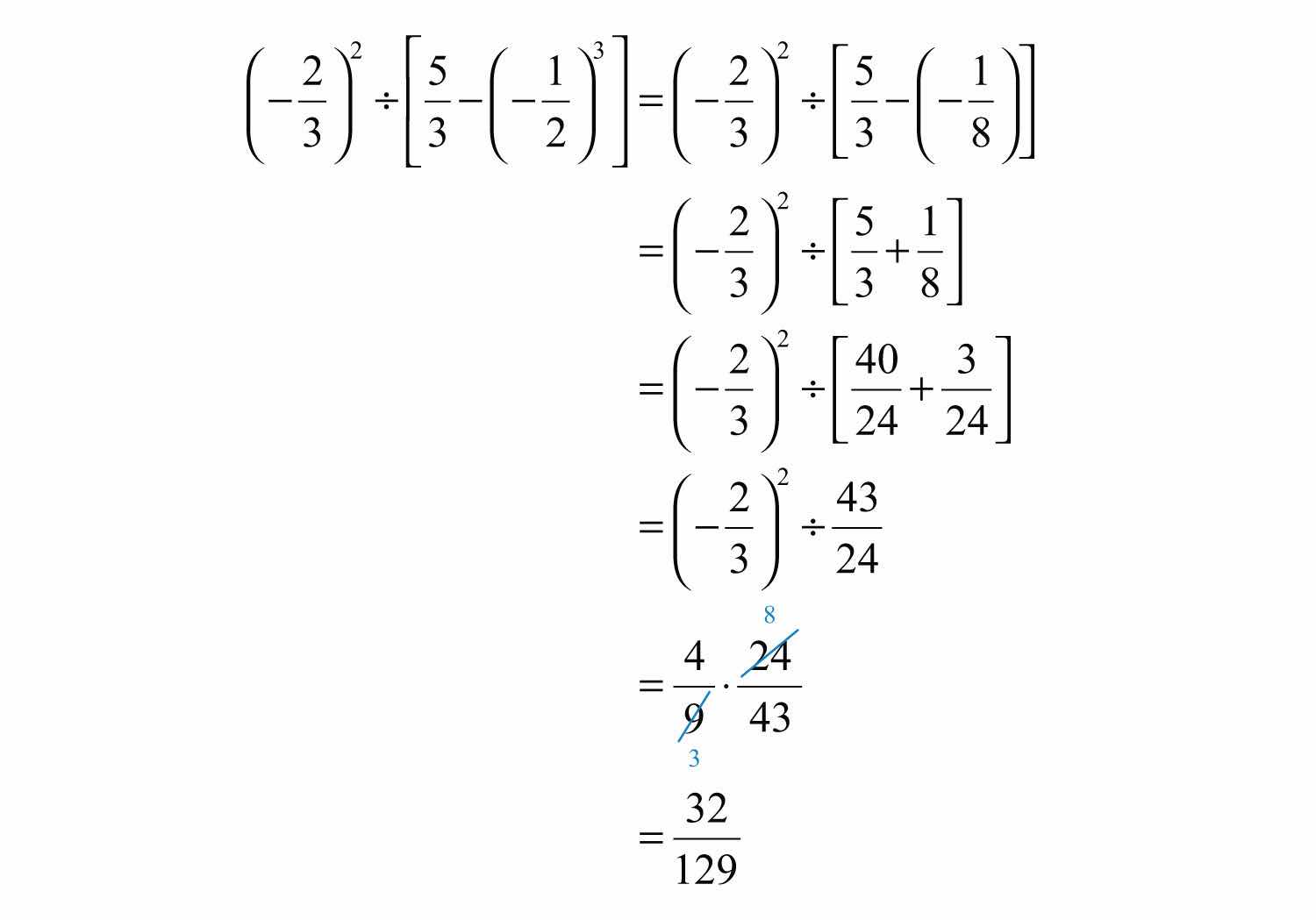
Answer: $\frac{32}{129}$

We are less likely to make a mistake if we work one operation at a time. Some problems may involve an absolute value, in which case we assign it the same order of precedence as parentheses.

Example 10: Simplify: $2 - 4 | - 4 - 3 | + {(- 2)}^{4}$ .

Solution: We begin by evaluating the absolute value and then the exponent ${(- 2)}^{4} = (- 2) (- 2) (- 2) (- 2) = + 16$ .

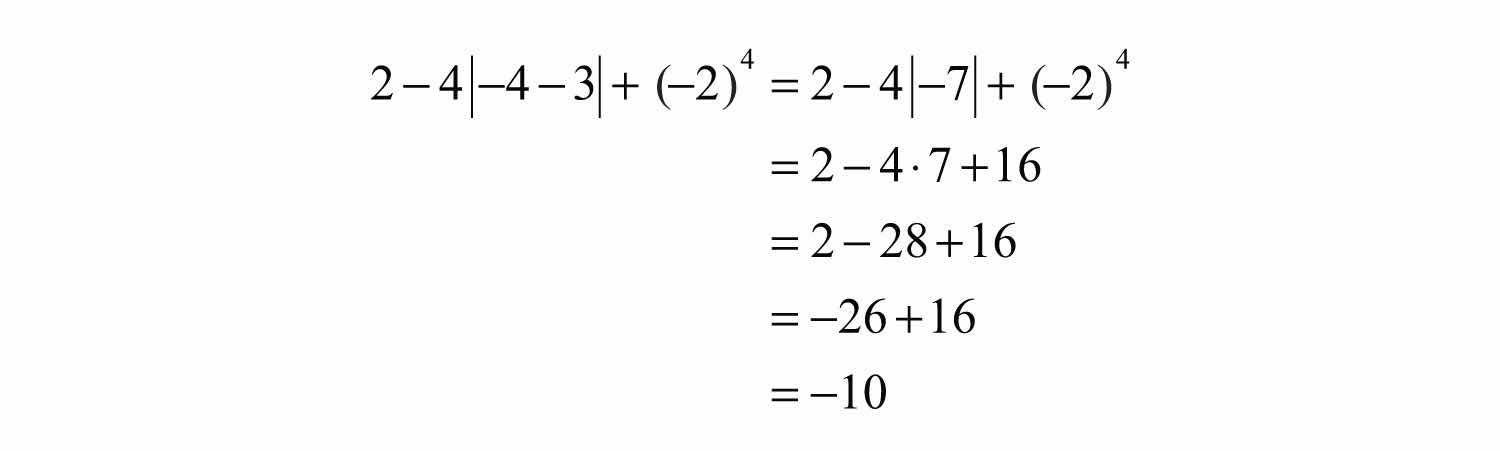
Answer: −10

Try this! Simplify: $10 \div 5 \cdot 2 | (- 4) + | - 3 | | + {(- 3)}^{2}$ .

Answer: 13

Video Solution

(click to see video)

Key Takeaways

Grouping symbols indicate which operations to perform first. We usually group mathematical operations with parentheses, brackets, braces, and the fraction bar. We also group operations within absolute values. All groupings have the same order of precedence: the operations within the innermost grouping are performed first.
When applying operations within a calculation, follow the order of operations to ensure a single correct result.
1. Address innermost parentheses or groupings first.
2. Simplify all exponents.
3. Perform multiplication and division operations from left to right.
4. Finally, perform addition and subtraction operations from left to right.
It is important to highlight the fact that multiplication and division operations should be applied as they appear from left to right. It is a common mistake to always perform multiplication before division, which, as we have seen, in some cases produces incorrect results.

Topic Exercises

Part A: Order of Operations

Simplify.

1. $- 7 - 3 \cdot 5$

2. $3 + 2 \cdot 3$

3. $- 3 (2) - 6^{2}$

4. $2 {(- 3)}^{2} + 5 (- 4)$

5. $6 / 3 * 2$

6. $6 / (3 * 2)$

7. $- \frac{1}{2} - \frac{3}{5} \cdot \frac{2}{3}$

8. $\frac{5}{8} \div \frac{1}{2} - \frac{5}{6}$

9. ${3.2}^{2} - 6.9 \div 2.3$

10. $8.2 - 3 \div 1.2 \cdot 2.1$

11. $2 + 3 (- 2) - 7$

12. $8 \div 2 - 3 \cdot 2$

13. $3 + 6^{2} \div 12$

14. $5 - 4^{2} \div (- 8)$

15. $- 9 - 3 \cdot 2 \div 3 (- 2)$

16. $- 2 - 3^{2} + {(- 2)}^{2}$

17. $12 \div 6 \cdot 2 - 2^{2}$

18. $4 \cdot 3 \div 12 \cdot 2 - {(- 2)}^{2}$

19. ${(- 5)}^{2} - 2 {(5)}^{2} \div 10$

20. $- 3 (4 - 7) + 2$

21. ${(- 2 + 7)}^{2} - 10^{2}$

22. $10 - 7 (3 + 2) + 7^{2}$

23. $- 7 - 3 (4 - 2 \cdot 8)$

24. $5 - 3 [6 - (2 + 7)]$

25. $1 + 2 [{(- 2)}^{3} - {(- 3)}^{2}]$

26. $- 3 [2 (7 - 5) \div 4 \cdot (- 2) + {(- 3)}^{3}]$

27. $- 7^{2} - [- 20 - {(- 3)}^{2}] - (- 10)$

28. $4.7 - 3.2 (4 - {1.2}^{3})$

29. $- 5.4 (6.1 - 3.1 \div 0.1) - {8.2}^{2}$

30. $- {7.3}^{2} + {(- 9.3)}^{2} - 37.8 \div 1.8$

31. $2 - 7 (3^{2} - 3 + 4 \cdot 3)$

32. ${(\frac{1}{2})}^{2} - {(- \frac{2}{3})}^{2}$

33. ${(\frac{1}{2})}^{3} + {(- 2)}^{3}$

34. ${(- \frac{1}{3})}^{2} - {(- \frac{2}{3})}^{3}$

35. $\frac{1}{3} - \frac{1}{2} \cdot \frac{1}{5}$

36. $\frac{5}{8} \div \frac{3}{2} \cdot \frac{14}{15}$

37. $5 \cdot \frac{2}{15} - {(\frac{1}{2})}^{3}$

38. $\frac{5}{17} (\frac{3}{5} - \frac{4}{35})$

39. $\frac{3}{16} \div (\frac{5}{12} - \frac{1}{2} + \frac{2}{3}) \cdot 4$

40. ${(\frac{2}{3})}^{2} - {(\frac{1}{2})}^{2}$

41. $\frac{1}{2} {[\frac{3}{4} \cdot {(- 4)}^{2} - 2]}^{2}$

42. $6 \cdot [{(\frac{2}{3})}^{2} - {(\frac{1}{2})}^{2}] \div {(- 2)}^{2}$

43. $\frac{{(- 5)}^{2} + 3^{2}}{- 4^{2} + 2 \cdot 7}$

44. $\frac{(- 3.2 - 3.3) (8.7 - 4.7)}{(- 4.7 + 3.9 + 2.1)}$

45. $\frac{2 - [3 - {(5 - 7)}^{2}]}{3 (6 - 3^{2})}$

46. $\frac{2 + 3 \cdot 6 - 4 \cdot 3}{2^{2} - 3^{2}}$

47. $\frac{(2 + 7) \cdot 2 - 2^{3}}{10 + 9^{2} + 3^{3}}$

48. $\frac{{(- 1 - 3)}^{2} - 15}{- 3 \cdot (- 7 + 2^{2}) - 5}$

49. $(7 + 4 * (- 2)) / (- 3 + (- 2)^2)$

50. $4 + 3 * ((- 3)^3 + 5^2) / 6 - 2^2$

51. Mary purchased 14 bottles of water at $0.75 per bottle, 4 pounds of assorted candy at $3.50 per pound, and 16 packages of microwave popcorn costing $0.50 each for her party. What was her total bill?

52. Joe bought four 8-foot 2-by-4 boards for $24.00. How much did he spend per linear foot?

53. Margaret bought two cases of soda at the local discount store for $23.52. If each case contained 24 bottles, how much did she spend per bottle?

54. Billy earns $12.00 per hour and “time and a half” for every hour he works over 40 hours a week. What is his pay for 47 hours of work this week?

55. Audry bought 4 bags of marbles each containing 15 assorted marbles. If she wishes to divide them up evenly between her 3 children, how many will each child receive?

56. Mark and Janet carpooled home from college for the Thanksgiving holiday. They shared the driving, but Mark drove twice as far as Janet. If Janet drove 135 miles, then how many miles was the entire trip?

Part B: Order of Operations with Absolute Values

Simplify.

57. $3 + 2 | - 5 |$

58. $9 - 4 | - 3 |$

59. $- (- | 2 | + | - 10 |)$

60. $- (| - 6 | - | - 8 |)$

61. $| - (40 - | - 22 |) |$

62. $| | - 5 | - | 10 | |$

63. $- {(| - 8 | - 5)}^{2}$

64. ${(| - 1 | - | - 2 |)}^{2}$

65. $- 4 + 2 | 2^{2} - 3^{2} |$

66. $- 10 - | 4 - 5^{2} |$

67. $- | {(- 5)}^{2} + 4^{2} \div 8 |$

68. $- (- 3 - [6 - | - 7 |])$

69. $- 2 [7 - (4 + | - 7 |)]$

70. $3 - 7 | - 2 - 3 | + 4^{3}$

71. $7 - 5 | 6^{2} - 5^{2} | + {(- 7)}^{2}$

72. ${(- 4)}^{2} - | - 5 + {(- 2)}^{3} | - 3^{2}$

73. $\frac{2}{3} - | \frac{1}{2} - {(- \frac{4}{3})}^{2} |$

74. $- 30 | \frac{10}{3} - \frac{1}{2} \div \frac{1}{5} |$

75. ${(- 4)}^{3} - (2 - | - 4 |) \div | - 3^{2} + 7 |$

76. $[10 - 3 (6 - | - 8 |)] \div 4 - 5^{2}$

Find the distance between the given numbers on a number line.

77. $\frac{1}{2}$ and $- \frac{1}{4}$

78. $- \frac{3}{4}$ and $- \frac{2}{3}$

79. $- \frac{5}{8}$ and $- \frac{3}{4}$

80. $- \frac{7}{5}$ and $\frac{3}{7}$

81. −0.5 and 8.3

82. 10.7 and −2.8

83. $3 \frac{1}{5}$ and $- 2 \frac{1}{3}$

84. $5 \frac{3}{4}$ and $0$

Part C: Discussion Board Topics

85. Convert various examples in this section to equivalent expressions using text-based symbols.

86. What is PEMDAS and what is it missing?

87. Discuss the importance of proper grouping and give some examples.

88. Experiment with the order of operations on a calculator and share your results.

Answers

1: −22

3: −42

5: 4

7: $- \frac{9}{10}$

9: 7.24

11: −11

13: 6

15: −5

17: 0

19: 20

21: −75

23: 29

25: −33

27: −10

29: 67.22

31: −124

33: $- \frac{63}{8}$

35: $\frac{7}{30}$

37: $\frac{13}{24}$

39: $\frac{9}{7}$

41: 50

43: −17

45: $- \frac{1}{3}$

47: $\frac{5}{59}$

49: −1

51: $32.50

53: $0.49

55: 20 marbles

57: 13

59: −8

61: 18

63: −9

65: 6

67: −27

69: 8

71: 1

73: $- \frac{11}{18}$

75: −63

77: $\frac{3}{4}$ unit

79: $\frac{1}{8}$ unit

81: 8.8 units

83: $5 \frac{8}{15}$ units