Reducing

A fractionA rational number written as a quotient of two integers: $\frac{a}{b}$, where b is nonzero. is a real number written as a quotient, or ratioRelationship between two numbers or quantities usually expressed as a quotient., of two integers a and b, where $b\ne 0$.

The integer above the fraction bar is called the numeratorThe number above the fraction bar. and the integer below is called the denominatorThe number below the fraction bar.. The numerator is often called the “part” and the denominator is often called the “whole.” Equivalent fractionsTwo equal fractions expressed using different numerators and denominators. are two equal ratios expressed using different numerators and denominators. For example,

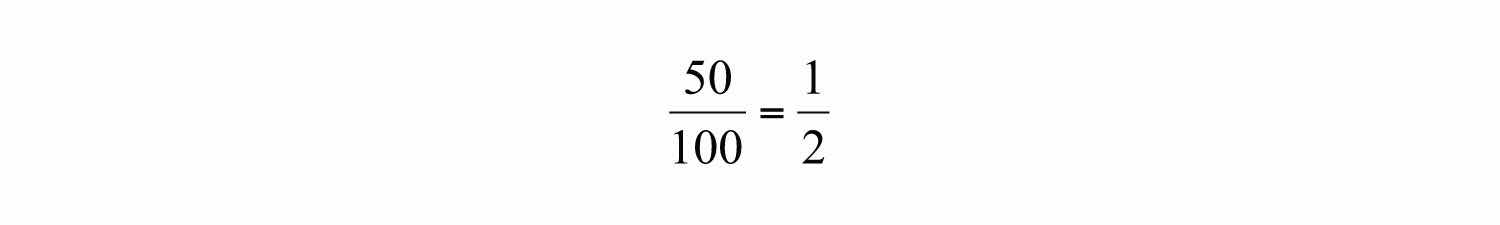
Fifty parts out of 100 is the same ratio as 1 part out of 2 and represents the same real number. Consider the following factorizations of 50 and 100:

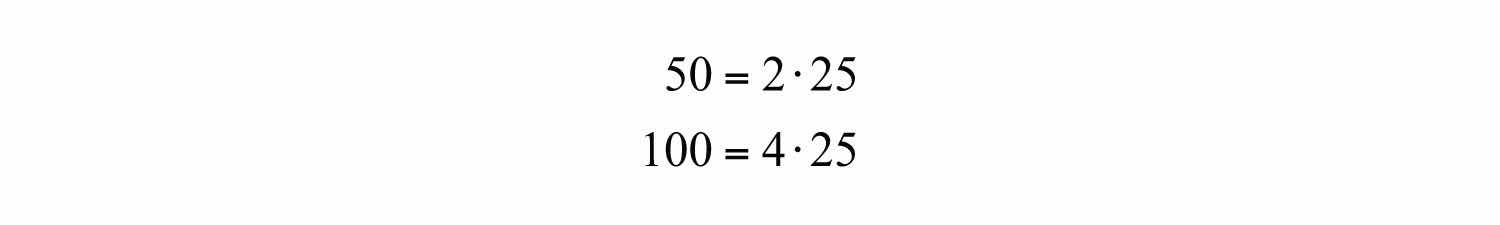
The numbers 50 and 100 share the factor 25. A shared factor is called a common factorA factor that is shared by more than one real number.. We can rewrite the ratio $\frac{50}{100}$ as follows:

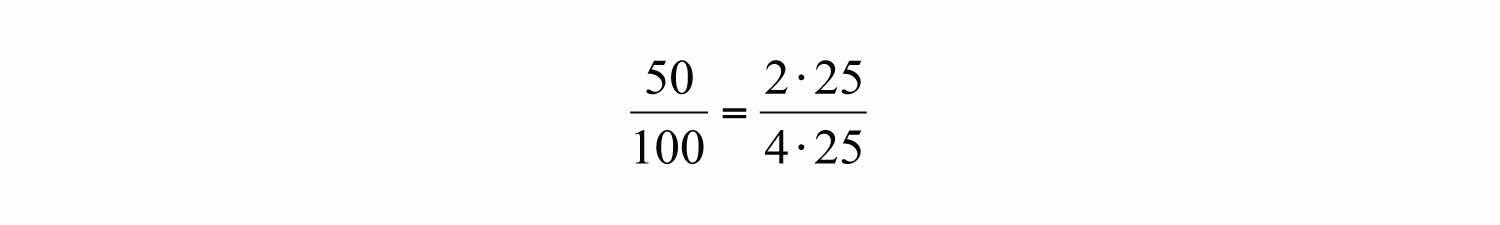
Making use of the multiplicative identity property and the fact that $\frac{25}{25}=1$, we have

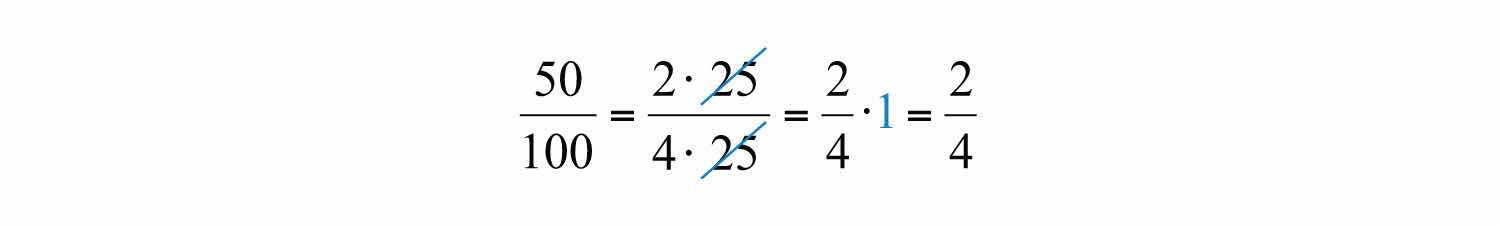
Dividing $\frac{25}{25}$ and replacing this factor with a 1 is called cancelingThe process of dividing out common factors in the numerator and the denominator.. Together, these basic steps for finding equivalent fractions define the process of reducingThe process of finding equivalent fractions by dividing the numerator and the denominator by common factors.. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by 25 as follows:

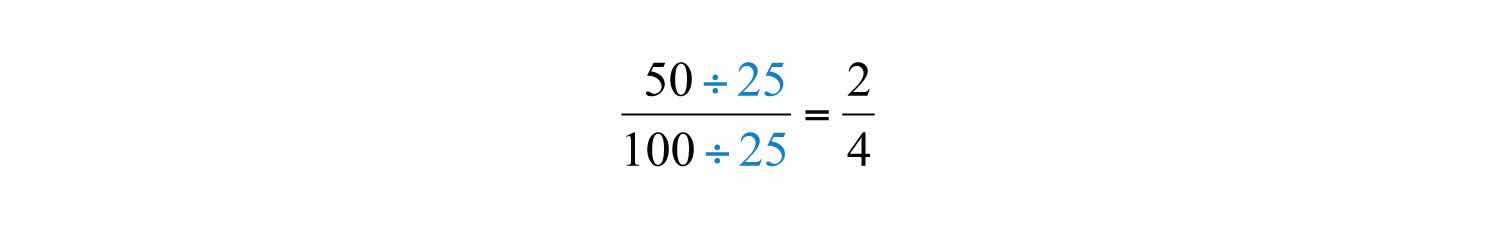
Finding equivalent fractions where the numerator and denominator have no common factor other than 1 is called reducing to lowest termsFinding equivalent fractions where the numerator and the denominator share no common integer factor other than 1.. When learning how to reduce to lowest terms, it is helpful to first rewrite the numerator and denominator as a product of primes and then cancel. For example,

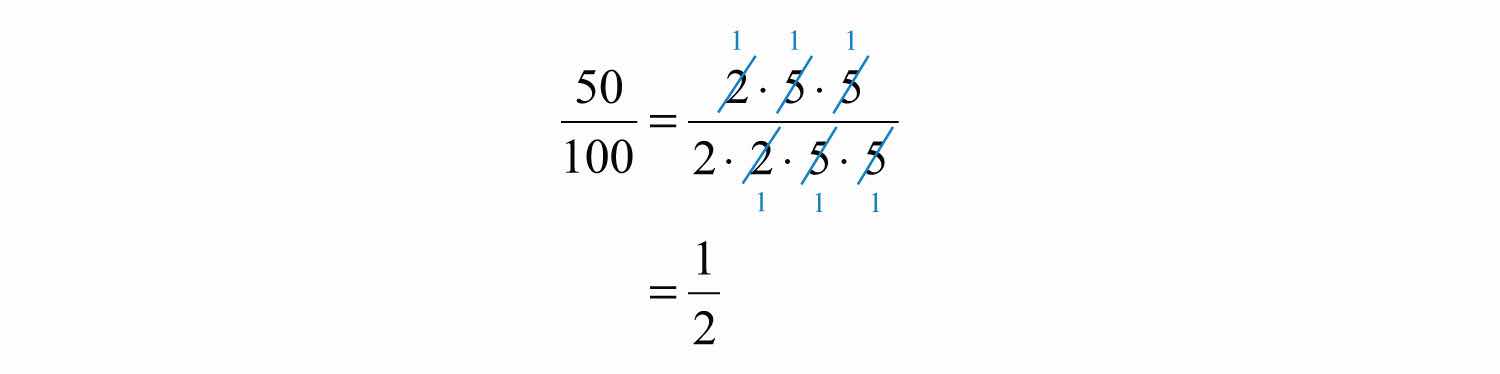
We achieve the same result by dividing the numerator and denominator by the greatest common factor (GCF)The largest shared factor of any number of integers.. The GCF is the largest number that divides both the numerator and denominator evenly. One way to find the GCF of 50 and 100 is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself.

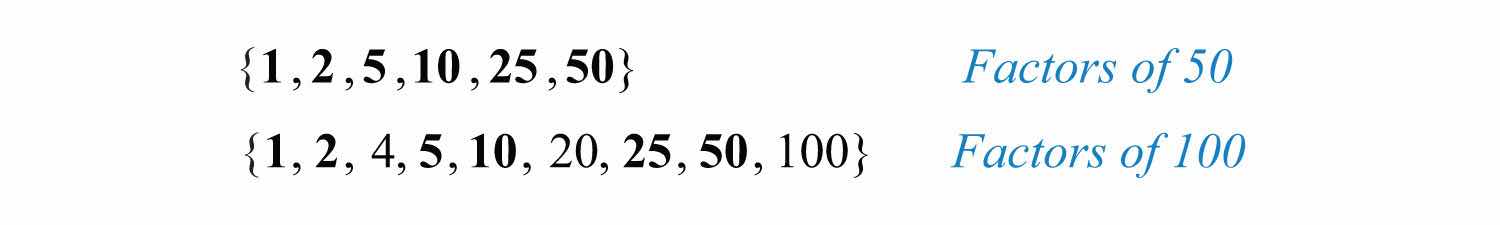
Common factors are listed in bold, and we see that the greatest common factor is 50. We use the following notation to indicate the GCF of two numbers: GCF(50, 100) = 50. After determining the GCF, reduce by dividing both the numerator and the denominator as follows:

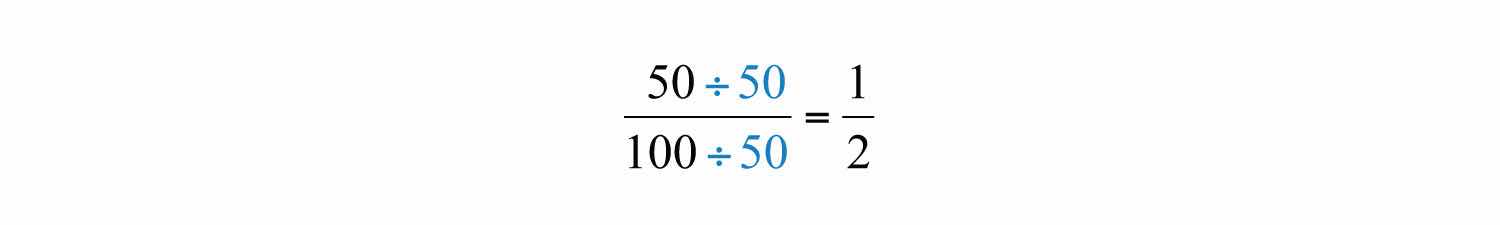
Example 1: Reduce to lowest terms: $\frac{105}{300}$.

Solution: Rewrite the numerator and denominator as a product of primes and then cancel.

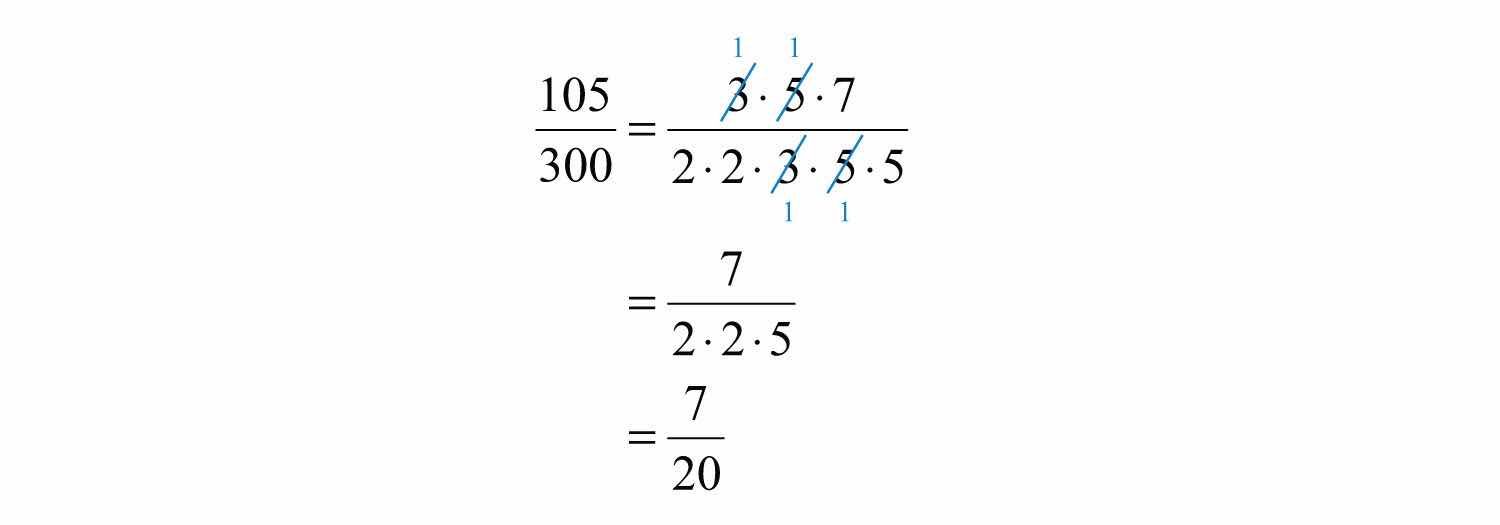
Alternatively, we achieve the same result if we divide both the numerator and denominator by the GCF(105, 300). A quick way to find the GCF of the two numbers requires us to first write each as a product of primes. The GCF is the product of all the common prime factors.

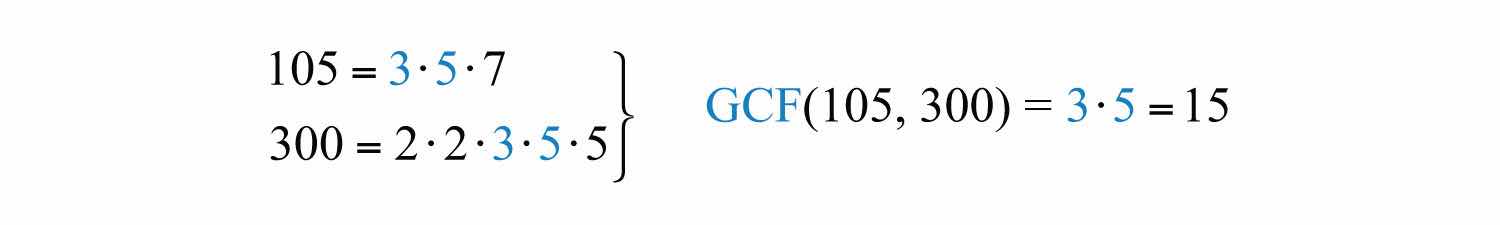
In this case, the common prime factors are 3 and 5 and the greatest common factor of 105 and 300 is 15.

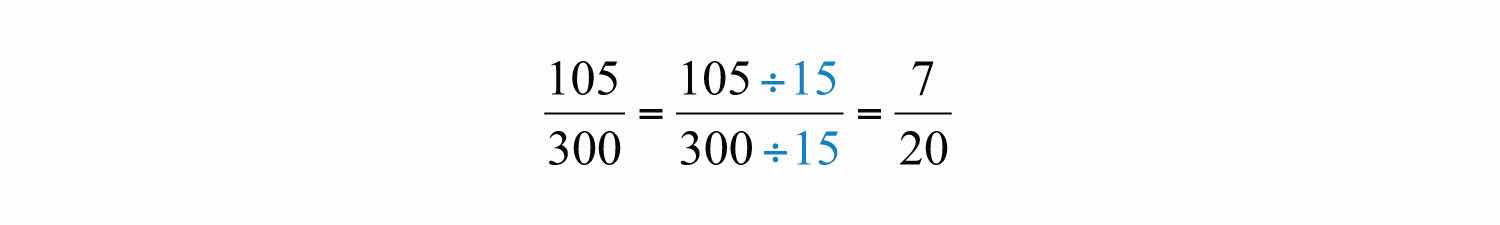
Answer: $\frac{7}{20}$

Try this! Reduce to lowest terms: $\frac{32}{96}$.

Answer: $\frac{1}{3}$

An improper fractionA fraction where the numerator is larger than the denominator. is one where the numerator is larger than the denominator. A mixed numberA number that represents the sum of a whole number and a fraction. is a number that represents the sum of a whole number and a fraction. For example, $5\frac{1}{2}$ is a mixed number that represents the sum $5+\frac{1}{2}$. Use long division to convert an improper fraction to a mixed number; the remainder is the numerator of the fractional part.

Example 2: Write $\frac{23}{5}$ as a mixed number.

Solution: Notice that 5 divides into 23 four times with a remainder of 3.

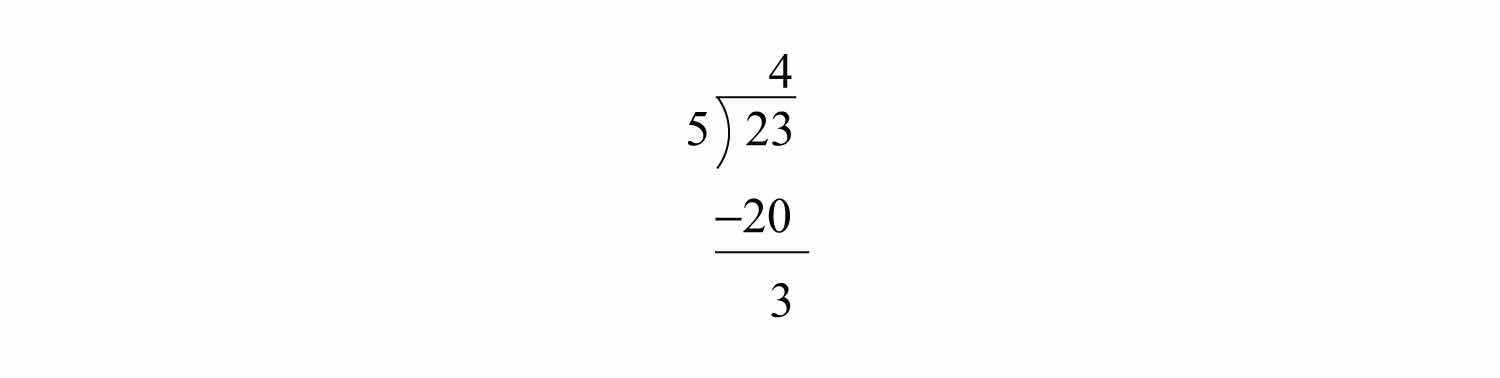
We then can write

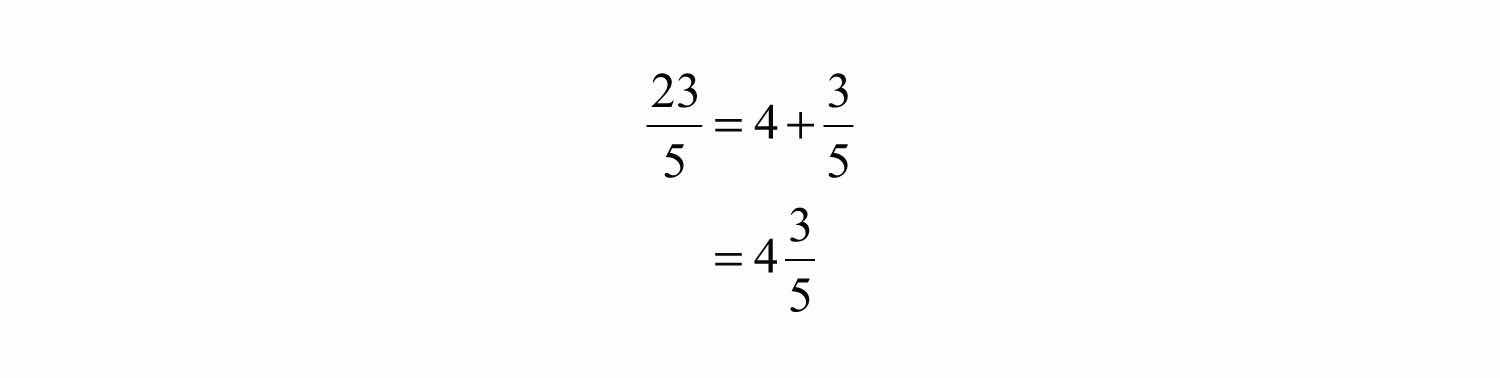
Note that the denominator of the fractional part of the mixed number remains the same as the denominator of the original fraction.

Answer: $4\frac{3}{5}$

To convert mixed numbers to improper fractions, multiply the whole number by the denominator and then add the numerator; write this result over the original denominator.

Example 3: Write $3\frac{5}{7}$ as an improper fraction.

Solution: Obtain the numerator by multiplying 7 times 3 and then add 5.

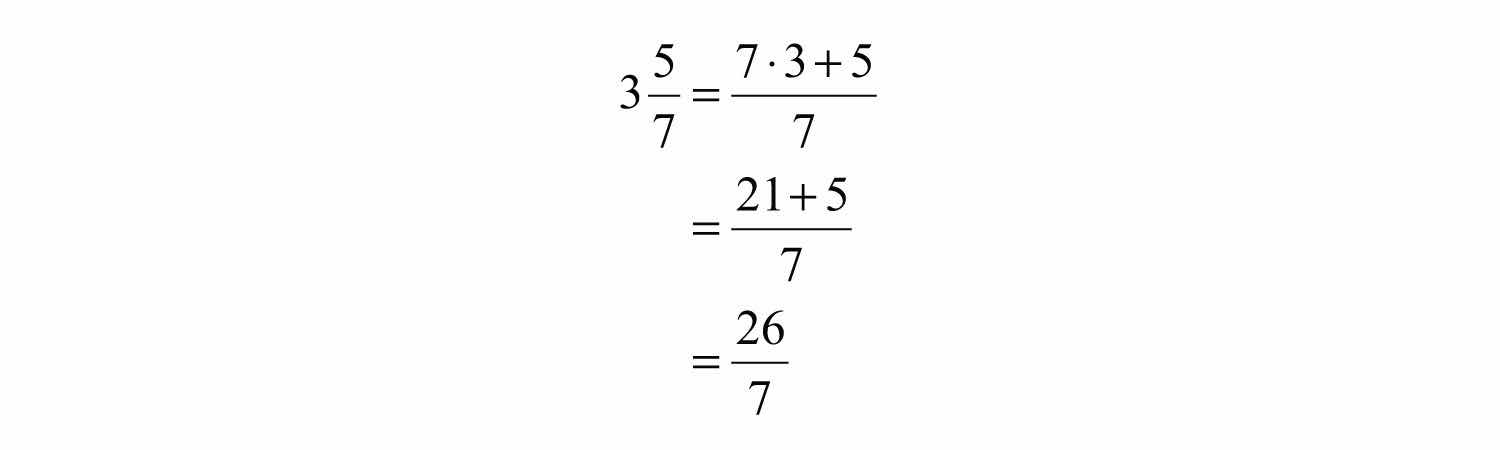
Answer: $\frac{26}{7}$

It is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as $\frac{26}{7}$, to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate.

Try this! Convert $10\frac{1}{2}$ to an improper fraction.

Answer: $\frac{21}{2}$

Multiplying and Dividing Fractions

In this section, assume that a, b, c, and d are all nonzero integers. The product of two fractions is the fraction formed by the product of the numerators and the product of the denominators. In other words, to multiply fractions, multiply the numerators and multiply the denominators:

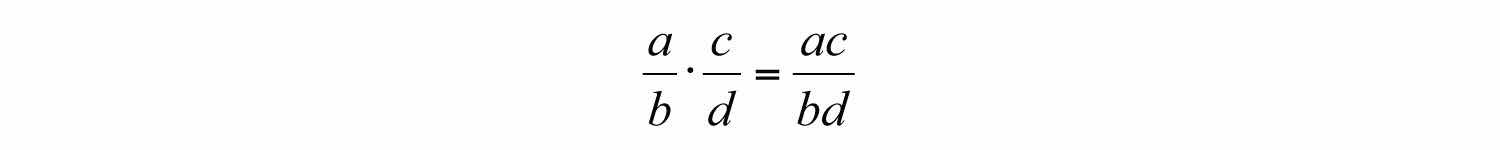
Example 4: Multiply: $\frac{2}{3}\cdot \frac{5}{7}$.

Solution: Multiply the numerators and multiply the denominators.

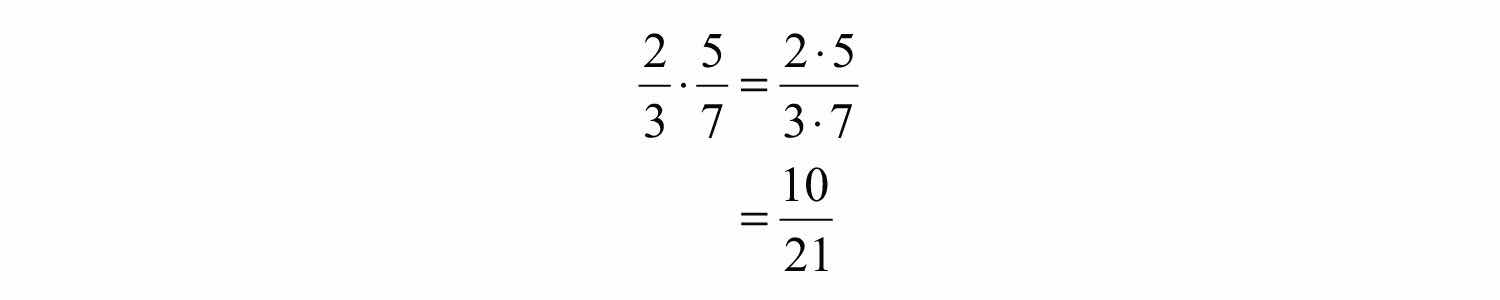
Answer: $\frac{10}{21}$

Example 5: Multiply: $\frac{5}{9}\left(-\frac{1}{4}\right)$.

Solution: Recall that the product of a positive number and a negative number is negative.

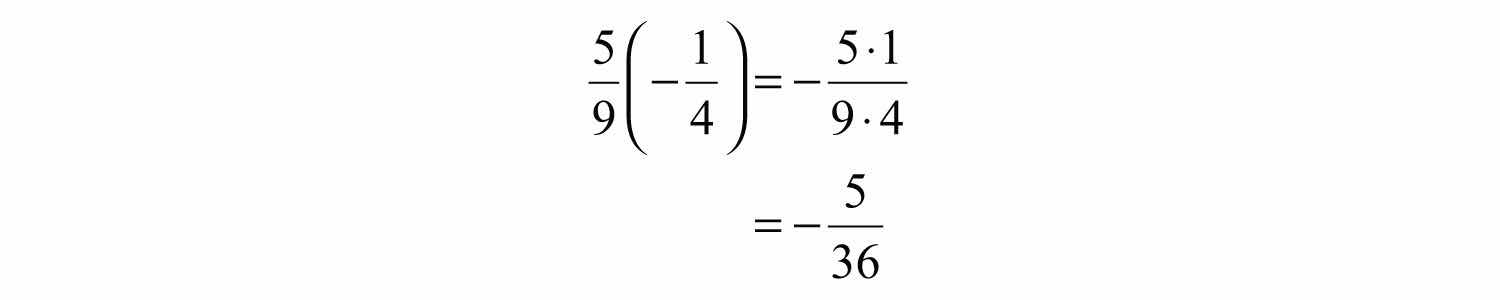
Answer: $-\frac{5}{36}$

Example 6: Multiply: $\frac{2}{3}\cdot 5\frac{3}{4}$.

Solution: Begin by converting $5\frac{3}{4}$ to an improper fraction.

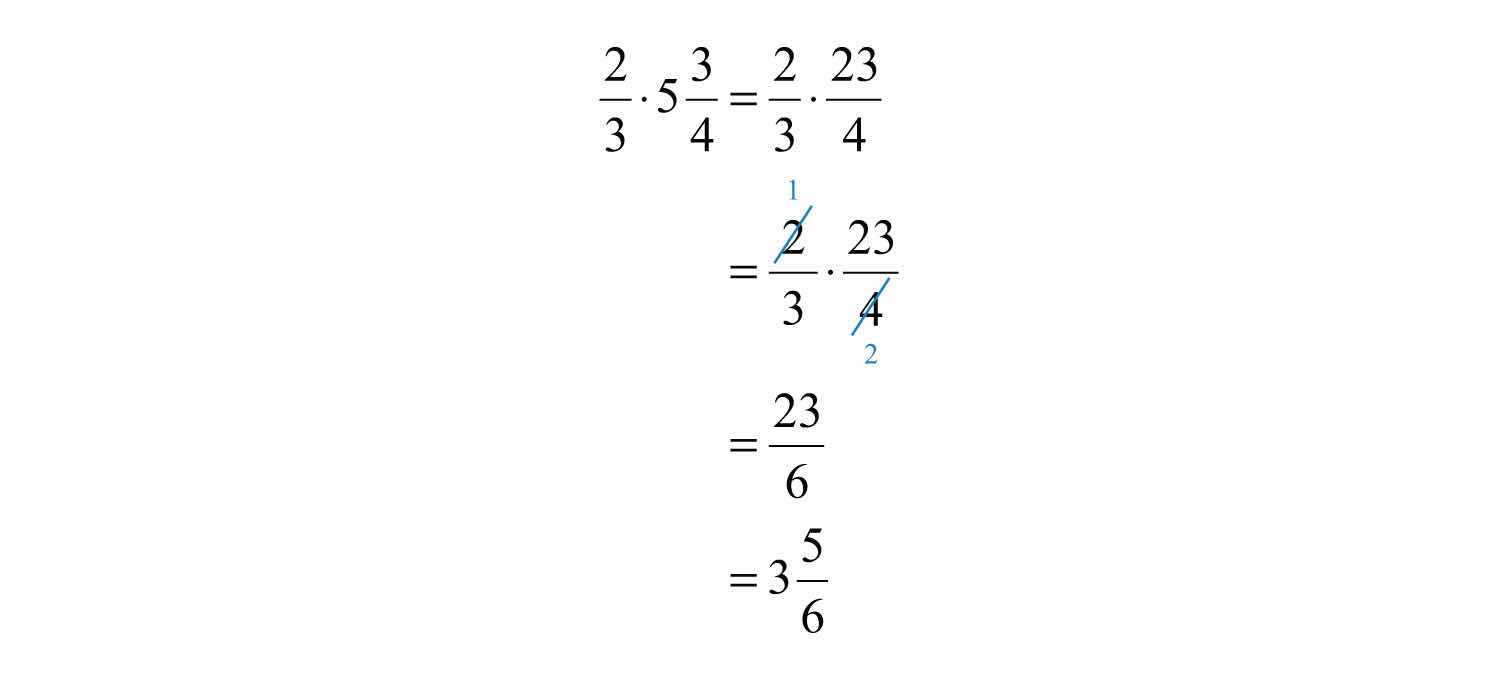
In this example, we noticed that we could reduce before we multiplied the numerators and the denominators. Reducing in this way is called cross cancelingCancelling common factors in the numerator and the denominator of fractions before multiplying., and can save time when multiplying fractions.

Answer: $3\frac{5}{6}$

Two real numbers whose product is 1 are called reciprocalsThe reciprocal of a nonzero number n is 1/n.. Therefore, $\frac{a}{b}$ and $\frac{b}{a}$ are reciprocals because $\frac{a}{b}\cdot \frac{b}{a}=\frac{ab}{ab}=1$. For example,

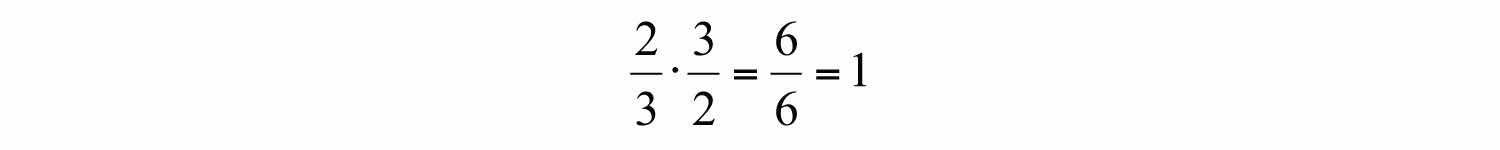
Because their product is 1, $\frac{2}{3}$ and $\frac{3}{2}$ are reciprocals. Some other reciprocals are listed below:

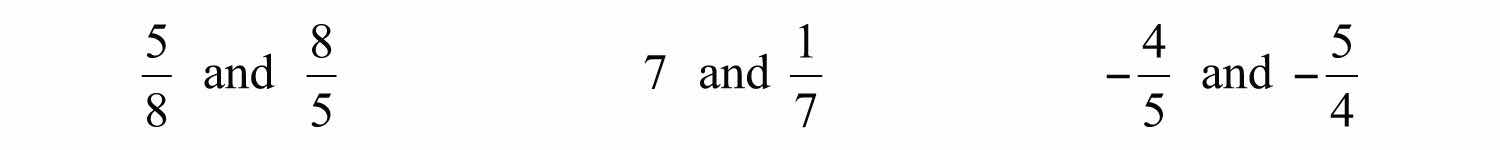
This definition is important because dividing fractions requires that you multiply the dividend by the reciprocal of the divisor.

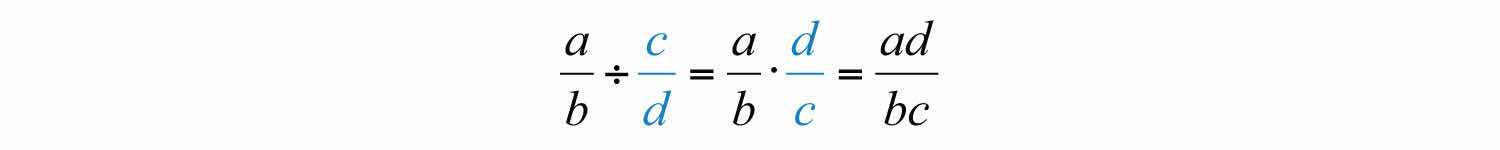
Example 7: Divide: $\frac{2}{3}÷\frac{5}{7}$.

Solution: Multiply $\frac{2}{3}$ by the reciprocal of $\frac{5}{7}$.

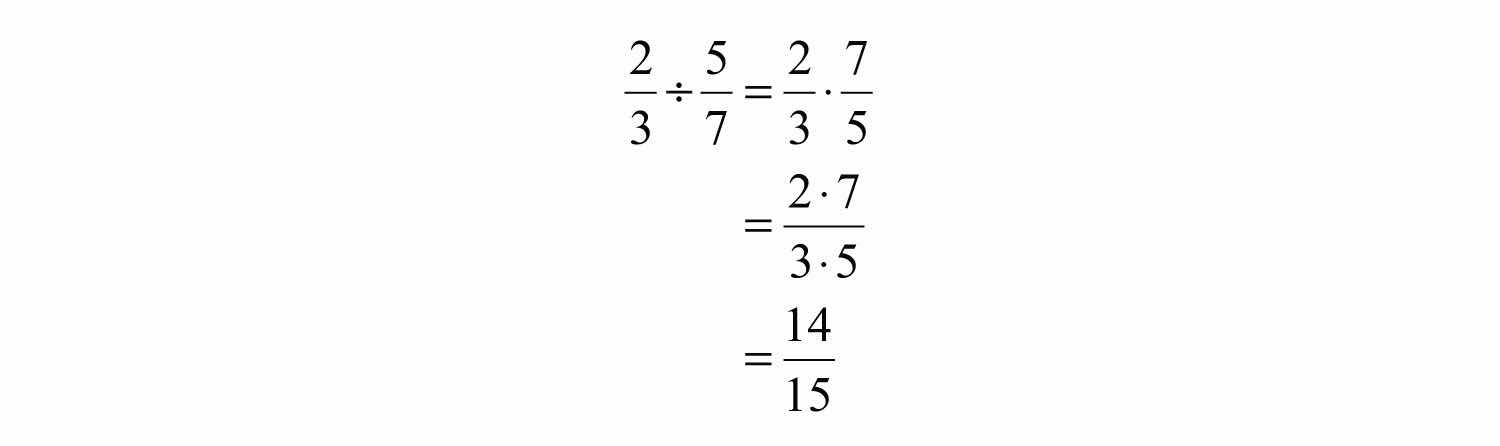
Answer: $\frac{14}{15}$

You also need to be aware of other forms of notation that indicate division: / and —. For example,

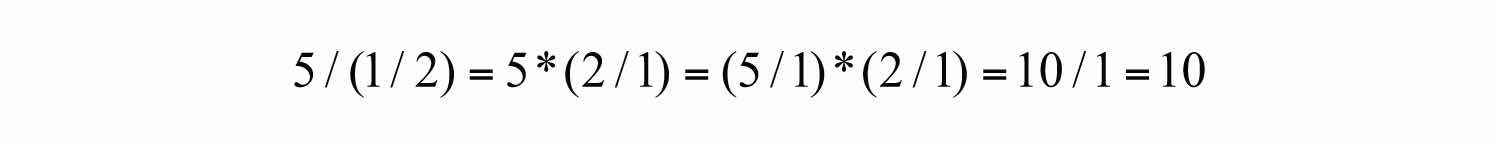
Or

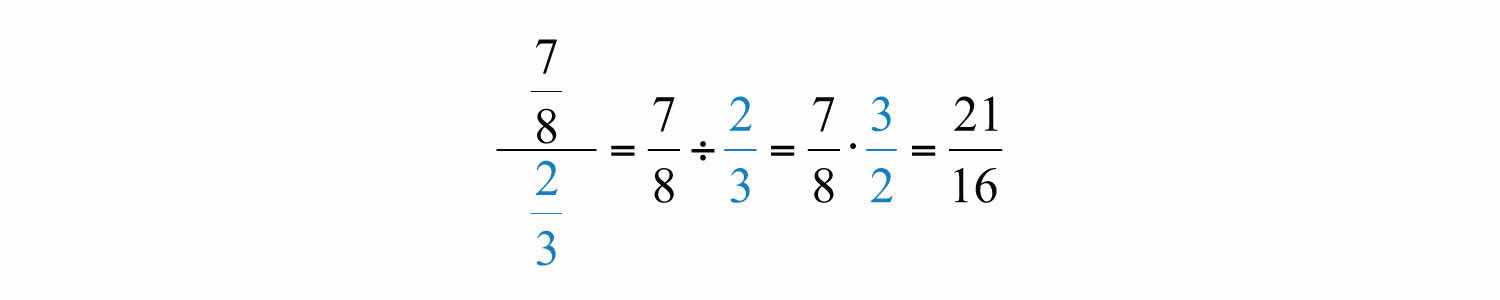
The latter is an example of a complex fractionA fraction where the numerator or denominator consists of one or more fractions., which is a fraction whose numerator, denominator, or both are fractions.

Note

Students often ask why dividing is equivalent to multiplying by the reciprocal of the divisor. A mathematical explanation comes from the fact that the product of reciprocals is 1. If we apply the multiplicative identity property and multiply numerator and denominator by the reciprocal of the denominator, then we obtain the following:

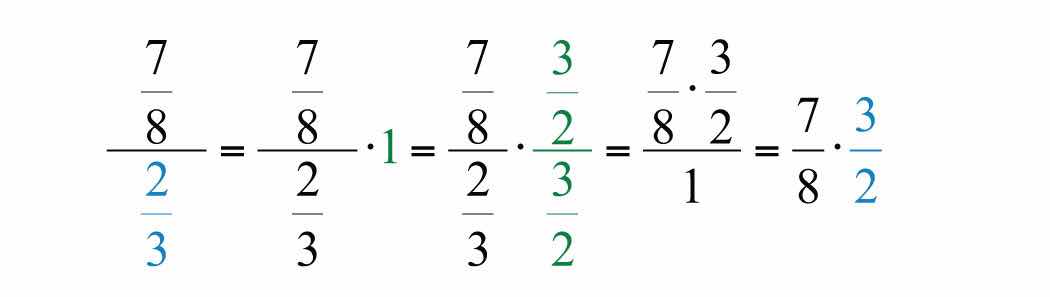
Before multiplying, look for common factors to cancel; this eliminates the need to reduce the end result.

Example 8: Divide: $\frac{\frac{5}{2}}{\frac{7}{4}}$.

Solution:

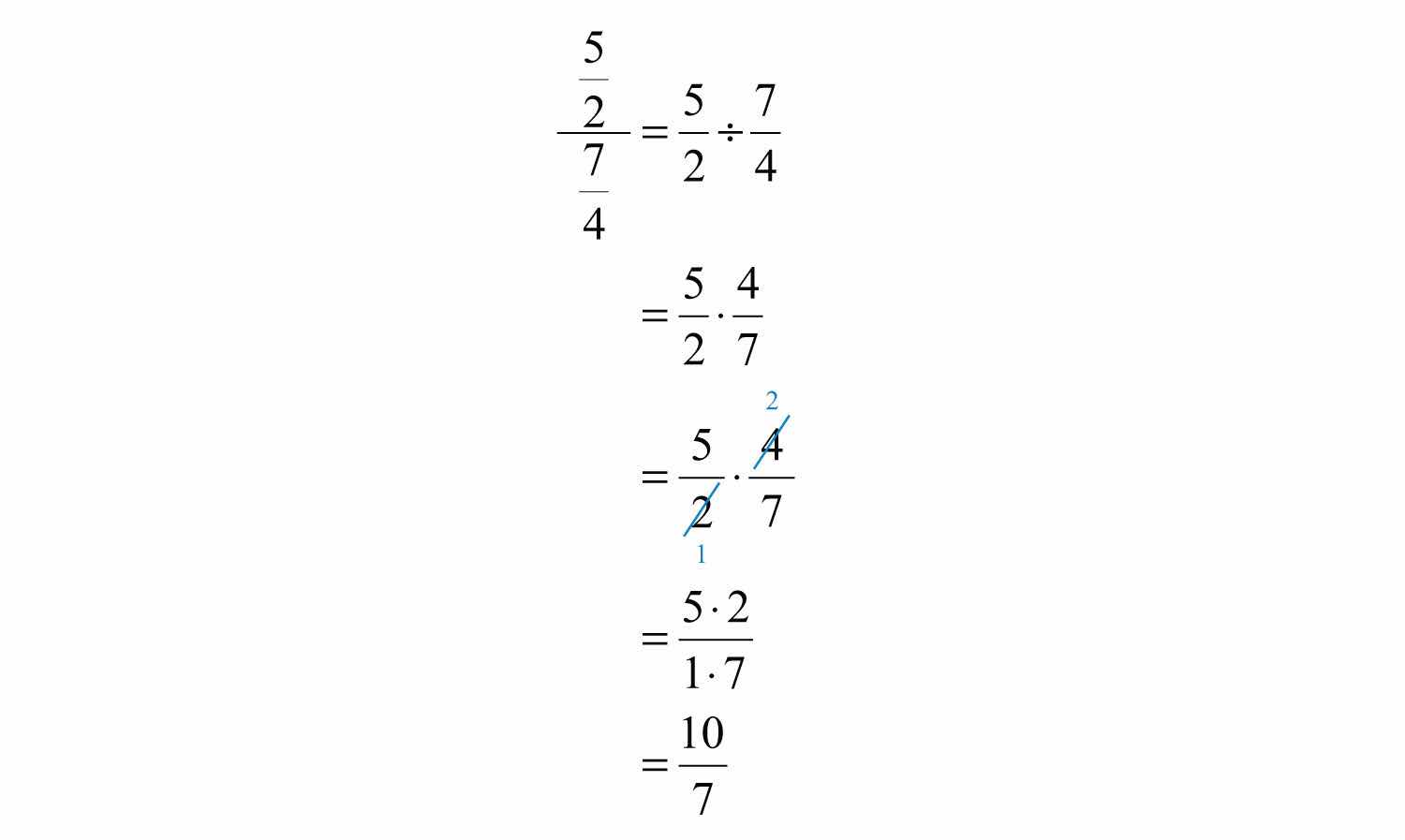
Answer: $\frac{10}{7}$

When dividing by an integer, it is helpful to rewrite it as a fraction over 1.

Example 9: Divide: $\frac{2}{3}÷6$.

Solution: Rewrite 6 as $\frac{6}{1}$ and multiply by its reciprocal.

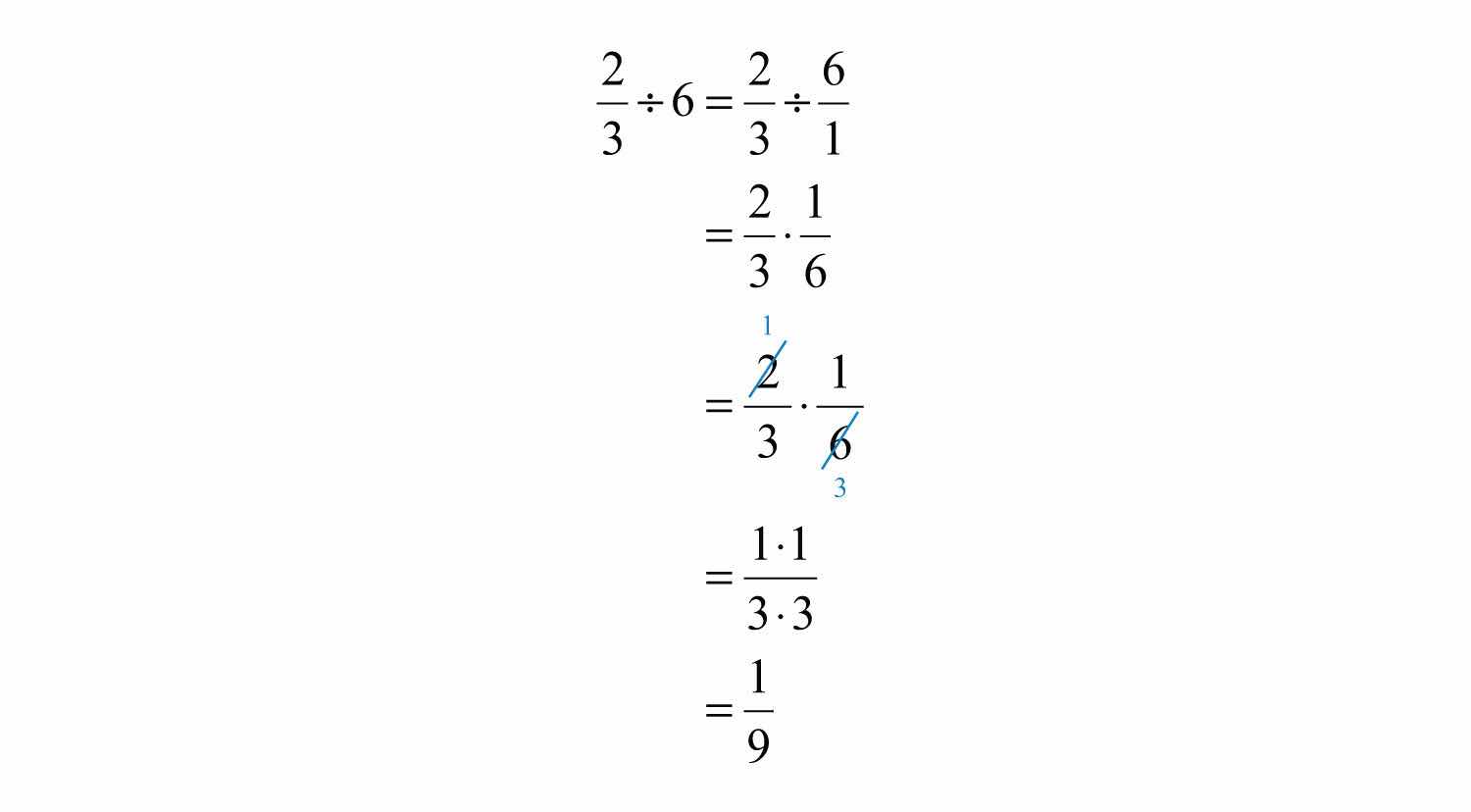
Answer: $\frac{1}{9}$

Also, note that we only cancel when working with multiplication. Rewrite any division problem as a product before canceling.

Try this! Divide: $5÷2\frac{3}{5}$.

Answer: $1\frac{12}{13}$

Adding and Subtracting Fractions

Negative fractions are indicated with the negative sign in front of the fraction bar, in the numerator, or in the denominator. All such forms are equivalent and interchangeable.

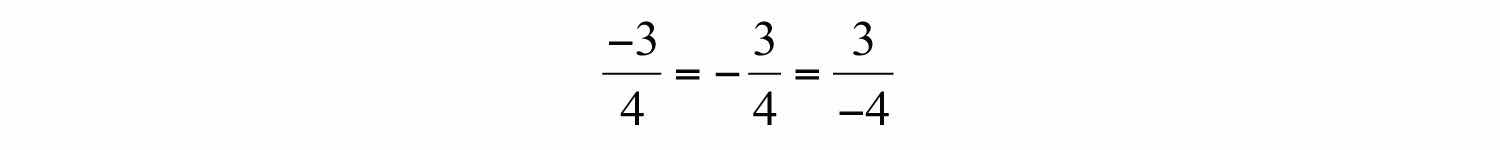
Adding or subtracting fractions requires a common denominatorA denominator that is shared by more than one fraction.. In this section, assume the common denominator c is a nonzero integer.

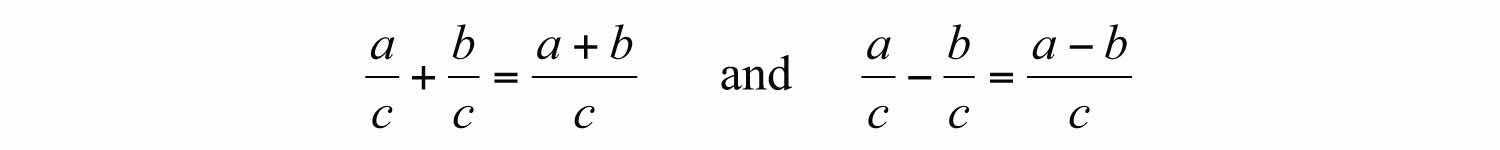
It is good practice to use positive common denominators by expressing negative fractions with negative numerators. In short, avoid negative denominators.

Example 10: Subtract: $\frac{12}{15}-\frac{3}{15}$.

Solution: The two fractions have a common denominator 15. Therefore, subtract the numerators and write the result over the common denominator:

Answer: $\frac{3}{5}$

Most problems that you are likely to encounter will have unlike denominatorsDenominators of fractions that are not the same.. In this case, first find equivalent fractions with a common denominator before adding or subtracting the numerators. One way to obtain equivalent fractions is to divide the numerator and the denominator by the same number. We now review a technique for finding equivalent fractions by multiplying the numerator and the denominator by the same number. It should be clear that 5/5 is equal to 1 and that 1 multiplied times any number is that number:

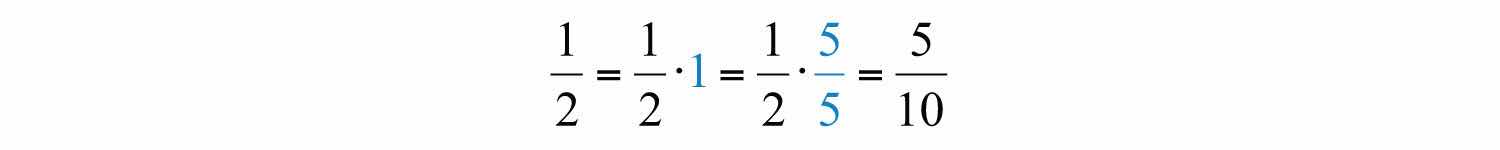
We have equivalent fractions $\frac{1}{2}=\frac{5}{10}$. Use this idea to find equivalent fractions with a common denominator to add or subtract fractions. The steps are outlined in the following example.

Example 11: Subtract: $\frac{7}{15}-\frac{3}{10}$.

Solution:

Step 1: Determine a common denominator. To do this, use the least common multiple (LCM)The smallest number that is evenly divisible by a set of numbers. of the given denominators. The LCM of 15 and 10 is indicated by LCM(15, 10). Try to think of the smallest number that both denominators divide into evenly. List the multiples of each number:

Common multiples are listed in bold, and the least common multiple is 30.

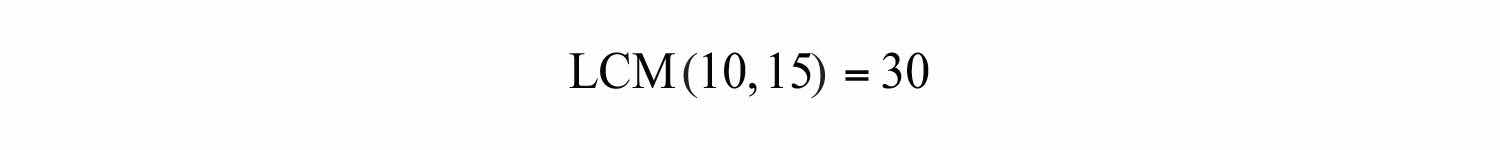
Step 2: Multiply the numerator and the denominator of each fraction by values that result in equivalent fractions with the determined common denominator.

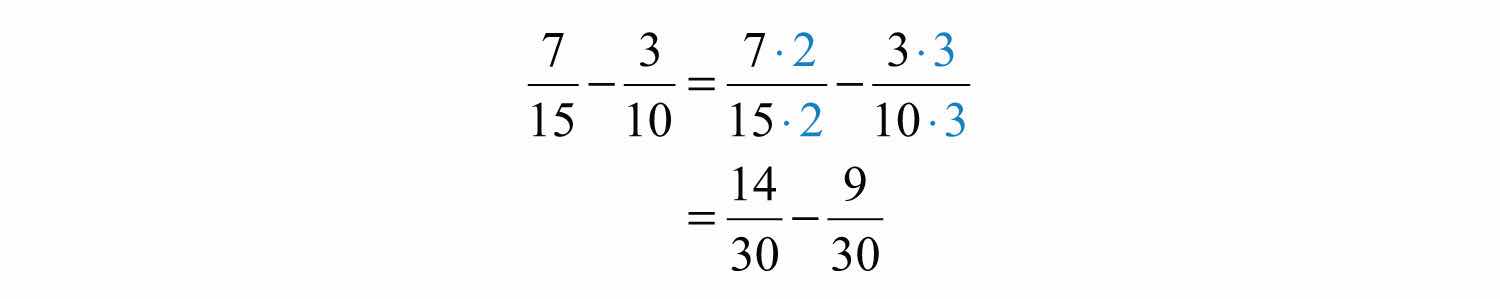
Step 3: Add or subtract the numerators, write the result over the common denominator and then reduce if possible.

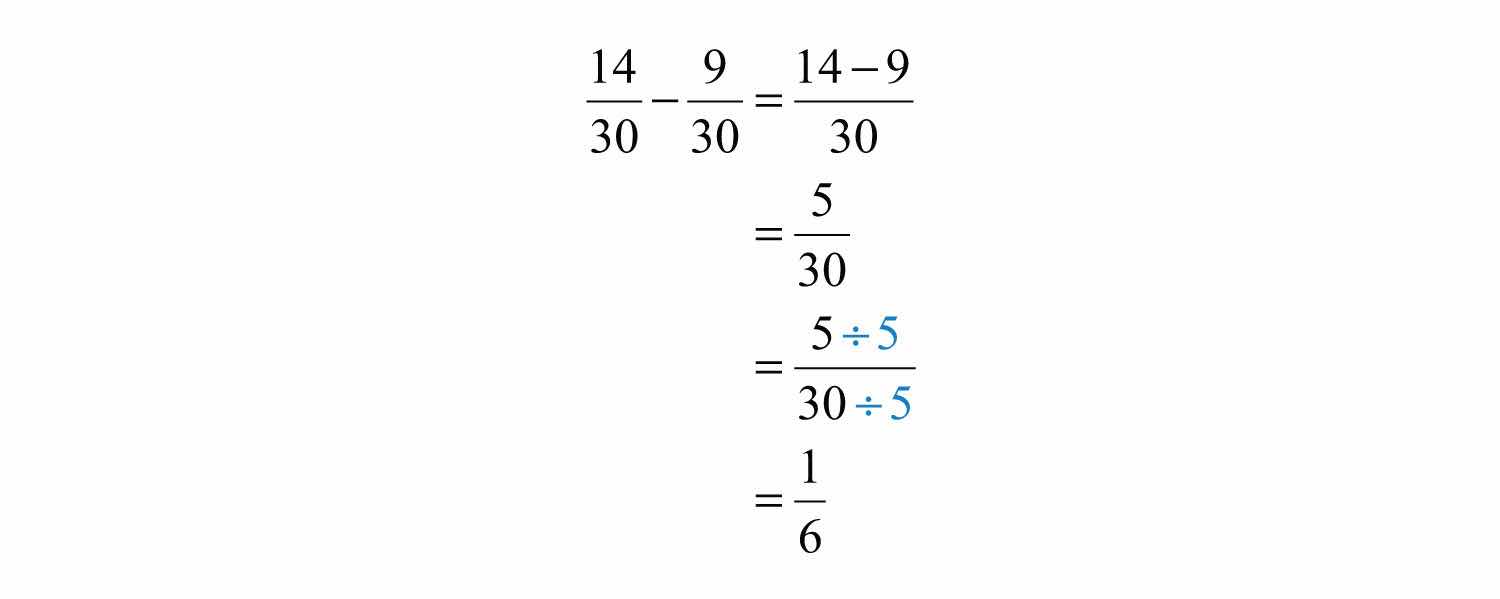
Answer: $\frac{1}{6}$

The least common multiple of the denominators is called the least common denominator (LCD)The least common multiple of a set of denominators.. Finding the LCD is often the difficult step. It is worth finding because if any common multiple other than the least is used, then there will be more steps involved when reducing.

Example 12: Add: $\frac{5}{10}+\frac{1}{18}$.

Solution: First, determine that the LCM(10, 18) is 90 and then find equivalent fractions with 90 as the denominator.

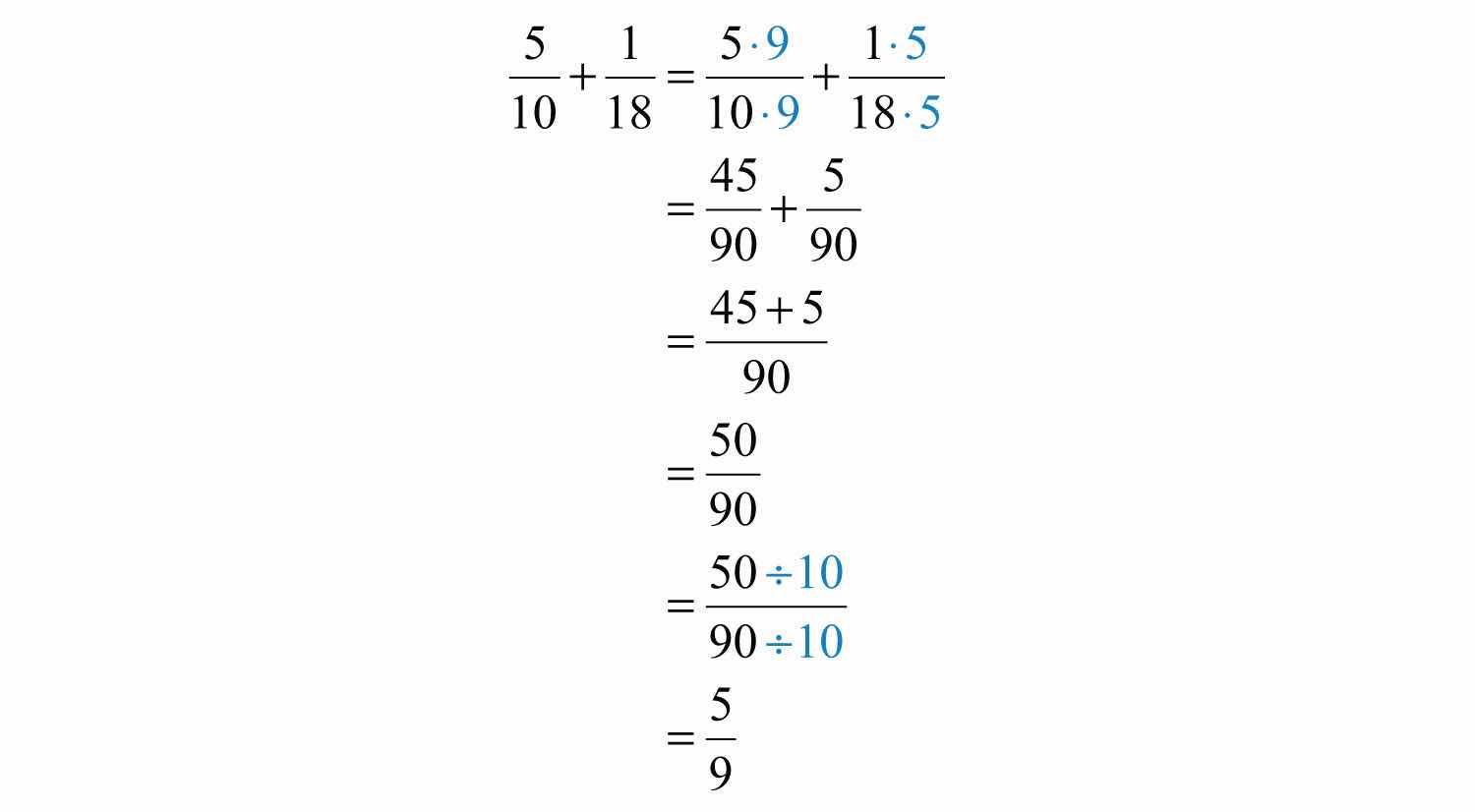
Answer: $\frac{5}{9}$

Try this! Add: $\frac{2}{30}+\frac{5}{21}$.

Answer: $\frac{32}{105}$

Example 13: Simplify: $2\frac{1}{3}+\frac{3}{5}-\frac{1}{2}$.

Solution: Begin by converting $2\frac{1}{3}$ to an improper fraction.

Answer: $2\frac{13}{30}$

In general, it is preferable to work with improper fractions. However, when the original problem involves mixed numbers, if appropriate, present your answers as mixed numbers. Also, mixed numbers are often preferred when working with numbers on a number line and with real-world applications.

Try this! Subtract: $\frac{5}{7}-2\frac{1}{7}$.

Answer: $-1\frac{3}{7}$

Example 14: How many $\frac{1}{2}$ inch thick paperback books can be stacked to fit on a shelf that is $1\frac{1}{2}$ feet in height?

Solution: First, determine the height of the shelf in inches. To do this, use the fact that there are 12 inches in 1 foot and multiply as follows:

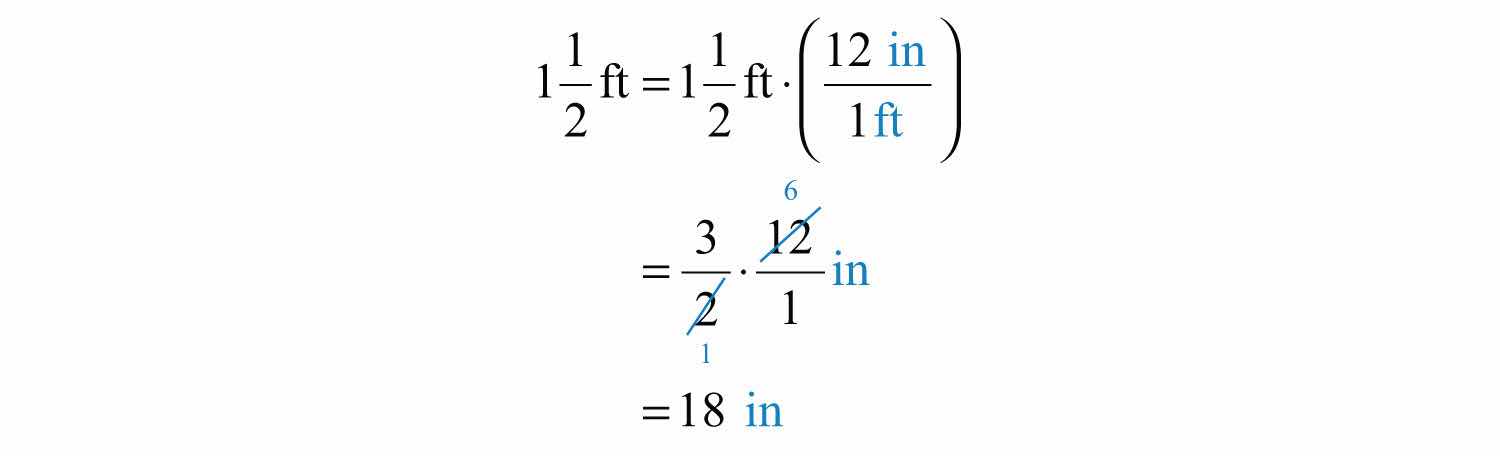
Next, determine how many notebooks will fit by dividing the height of the shelf by the thickness of each book.

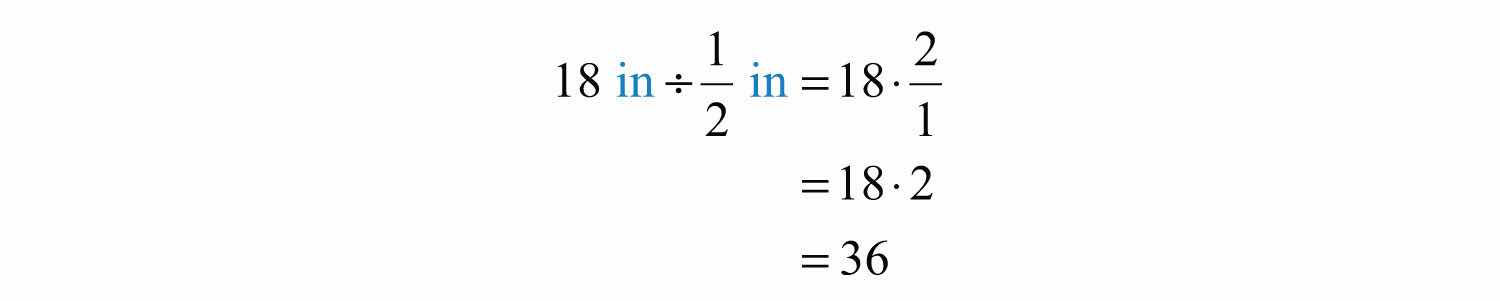
Answer: 36 books can be stacked on the shelf.