If the above player doesn't work, try this direct link.

Logarithms can help you solve exponential functions. In this lesson, you will learn about how to work with and recognize logarithms through an example about cell phones.

Quick Review of Exponentials

In a previous video, titled 'What is an Exponential Function,' we found out how we could model the number of cell phones there are with exactly that: an exponential function. We guessed that there were around 5 in 1981, but then there were twice as many each year. This gave us the exponential function y=5*2^x, where y was the number of cell phones there were, and x was the number of years that had happened since 1981, and it allowed us to say things like, 23 years after 1981 there were close to 42 million cell phones simply by plugging in 23 for x and multiplying out to figure out what y was.

Example #1

But what if, instead, I said I was from the future, and in my world there were over 171,000,000,000 cell phones? How far into the future am I from? Now, instead of substituting for x and figuring out what y is, we do the opposite and substitute in for y and try to figure out what x is. What I'm left with is an equation that I can use inverse operations to solve for. The first step is easy; I know I can undo multiplication with division. I divide both sides by 5 and I find that 2^x =34,000,000,000 or so. But now we need to undo an exponential.... uhhh, divide? No, division undoes multiplication. Square root? No, square root undoes the power of 2. We need to undo the power of x, but we haven't learned how to do that yet!

Undo an exponential.

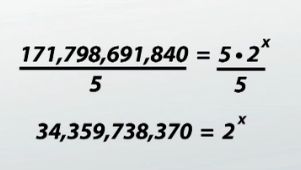The Logarithm

Enter the logarithm. Logarithms are the inverse operation to exponentials, and they are a quantity that represents the power to which the base must be raised to produce the given number. Okay, that's a mouthful, so let's take a closer look at what I just said. First, they are the inverse operation to exponentials. Just like addition and subtraction undo each other, or multiplication and division undo each other, logs and exponentials do, too.

Saying this in math might look something like this: if I assume that y+x=b, I can simply undo the y from both sides with subtraction to get an equivalent statement x=b-y. So I have one statement written with addition, and one statement written with subtraction that basically mean the same thing.

Undo the y from both sides with subtraction to get an equivalent statement x=b-y.

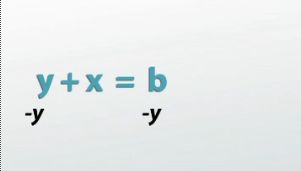I can do the same thing with multiplication and division. If I say that y*x=b, I can undo the 'times by y' with 'divide by y,' and I get a statement that says x=b/y. So that's a statement written with division. The first one was a statement written with multiplication, but they mean the same thing. They're equivalent.

It's exactly the same with exponentials. I can have a statement, y=b^x, but by taking the logb of both sides, I undo the exponential. The x is now by itself, and on the other side, I have log base b of y - log base b of y is the logarithmic form, while y=b^x is the exponential form, but they both are equivalent statements.

Looking at these two forms shows us the second thing I said during the wordy definition: logarithms are a quantity that represents the power to which the base must be raised to produce the given number. In other words, the answer to a log is the exponent that you raise the base to, to get to the number that you're taking the log of.

Back to Example #1

OK, now that that detour is over and we have the logarithm in our arsenal, we can get back to figuring out how far into the future I was with my 171 billion cell phones. We were here: 2^x=34,359,738,368. I can now undo the exponential base 2 by taking the log base 2 of both sides, because logs and exponentials are inverse operations. On the right-hand side of the equation, the log2 undoes the 2^x, and I just get x. On the left-hand side I now have the log2 of 34,359,738,370.

The answer to a log is the exponent that turns the base into the number you are taking the log of.

When you see this, you need to remind yourself that the answer to a log is the exponent that turns the base into the number you're taking the log of. Now, we'll learn some tricks and get some practice evaluating logs in future lessons, but for now let's cut to the chase and say that log2(34,359,738,370) is 35 … because 2^35 equals that 34,359,738,368 number. So because 35 is the power that turns the base of the log into the thing I'm taking the log of, that is my answer.

Lesson Summary

To review: logarithms and exponentials are inverse operations, which means they undo each other. If we have the exponential form y=b^x, we can write an equivalent expression in logarithmic form as logb(y)=x. This means that the answer to a log is the exponent that turns the base of the log into the thing we're taking the log of.