If the above player doesn't work, try this direct link.

Let's look at some more polynomial division problems. We will use long division and synthetic division, but this time we will have a couple of more involved problems. So get out some paper and a pencil and let's begin!

Polynomial Division

We have looked at some basic polynomial long division and synthetic division. Now let's look at a couple that are a little more complicated. They work exactly the same except we have larger divisors or parts of the dividend are missing.

Example #1

Here's our first example:

(x^3 - 9) ÷ (x^2 + 3)

Do you notice that we don't have an x^2 or x term in the dividend? We need to put something in as a place marker. Whenever we have a missing term, we will put in a zero as their coefficients. For example, in this problem we will have (x^3 + 0x^2 + 0x - 9). Why the zeros? Because anything multiplied by zero is zero. So we aren't adding anything to the problem!

Whenever there is a missing term, put in zero as their coefficients.

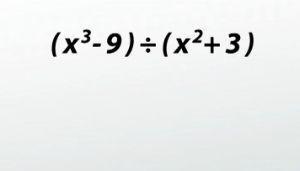To fill in our long division, we now have: (x^3 + 0x^2 + 0x - 9) as the dividend, so it goes under the long division symbol.

(x^2 + 3) is the divisor. Do you notice that it also has a missing term? Just like the dividend, we need to put in a place marker. So (x^2 + 0x + 3) goes in front of the long division symbol.

Now we're ready to start division. The steps are the same every time, and I think it's easier to show and talk about the steps than just listing them.

To find the first term of the quotient, we take the first terms of the divisor and dividend and divide them. So we have x^3 ÷ x^2. I like to write them as a fraction. It's easier to divide or reduce.

x^3/x^2 = x

x is the first term of the quotient. We write it above the long division symbol.

To figure out what we will subtract from the dividend, we multiply x times the divisor: (x^2 + 0x + 3).

x(x^2 + 0x + 3) = x^3 + 0x^2 + 3x

So that is written underneath the dividend, matching like terms.

Here's where I like to make my life easy. To subtract the polynomials, I just change the signs of their terms and add! So x^3 becomes -x^3, 0x^2 becomes -0x^2 and 3x becomes -3x. So now I'm going to add down.

x^3 - x^3 = 0

0x^2 - 0x^2 = 0

0x - 3x = -3x

Just like in long division we learned as kids, I'm going to bring down the -9. So now I have -3x - 9.

Now we have a predicament. x^2 doesn't go into -3x - 9! This turns out to be our remainder.

So what's our answer?

x + ((-3x - 9)/(x^2 + 3))

There isn't a need to put 0x as part of the denominator in the remainder.

Example #2

(2x^3 - 5 - 14x) ÷ (x + 3)

This one is almost ready for synthetic division. The divisor is a first-degree binomial with a leading coefficient of 1. Place the coefficients of the dividend under the symbol, just like in long division, but don't write the variables! Make sure to leave enough space between the numbers because we don't want to get the numbers confused.

Coefficients must be listed in descending order of exponent power.

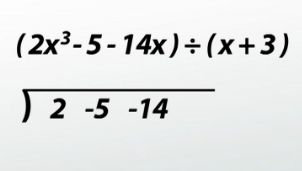Wait! Did you write it as you see it? Oh no! The dividend and divisor must be in descending order. What does that mean? We need to list the terms from the largest exponent to the smallest. Even if we're missing one, we need to put in a place marker.

So now we have: (2x^3 + 0x^2 - 14x - 5) ÷ (x + 3).

Always take the opposite of what you see in the divisor.

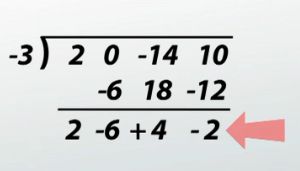
Next, look at (x + 3). We write -3 to the left of the long division symbol. Remember, you always take the opposite of what you see in the divisor.

Our first step is to bring down the leading coefficient, 2.

Multiply -3 times 2, which is -6. I write that under the 0. 0 + -6 is -6.

-3 times -6 is 18, and I write that under -14. I add down: -14 + 18 is 4, and I write that next to the -6.

I take -3 times 4, which is -12. I add down: 10 + -12 is -2, and it turns out that our remainder is -2. So we have -12 written under the 10. How do I know there's a remainder? Because our last term is not a 0.

The remainder is -2.

Great, Kathryn, but what is the answer going to look like?

In synthetic division, the degree of the final polynomial answer is one less than the dividend polynomial. Since 2x^3 - 5 - 14x is degree 3, our answer will be degree 2.

So my answer's going to be: 2x^2 - 6x + 4 with a remainder of -2. How am I going to write that?

Remember, the remainder has to be written as a fraction.

So my final answer's going to look like 2x^2 - 6x + 4 + (-2/(x + 3))

The final answer will look like this.

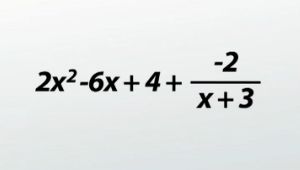Example #3

(6y^3 + 7y^2 - 5y + 5) ÷ (3y - 1)

To fill in our long division, (6y^3 + 7y^2 - 5y + 5) goes underneath the long division symbol. (3y - 1) is the divisor, so it goes in the front of the long division symbol.

Now we're ready to start the division. You might be asking yourself, 'Why aren't we using synthetic division?' Remember, the leading coefficient of our divisor has to be a 1. In this case, we have a 3, so synthetic division isn't going to work very easily.

To find the first term of the quotient, we take the first terms from the divisor and dividend and divide them: 6y^3 ÷ 3y. I like to write them as a fraction. It's easier to divide or reduce.

6y^3 ÷ 3y = 2y^2

2y^2 is the first term of the quotient. We write it above the long division symbol.

To figure out what we will subtract from the dividend, we multiply 2y^2 times the divisor, 3y - 1.

2y^2(3y - 1) = 6y^3 - 2y^2

To subtract the polynomials, I just change the signs of the terms and add! We'll have -6y^3 + 2y^2, and then we're going to add down.

6y^3 - 6y^3 = 0

7y^2 + 2y^2 = 9y^2

We're going to bring down our next term, which is -5y.

Now we're going to start all over again and take the first terms from the divisor and dividend. We're going to have 9y^2 ÷ 3y, and that turns out to be 3y.

To figure out what we will subtract from the dividend, we multiply 3y times the divisor, 3y - 1.

3y(3y - 1) = 9y^2 - 3y

We're going to write that under the dividend, matching like terms. We're going to change their signs and add down.

9y^2 - 9y^2 = 0

-5y + 3y = -2y

Finally, we're going to bring down this last 5. We're going to have -2y + 5. You'll notice that the dividend is now -2y + 5. Once again, we're going to take the leading coefficients of the divisor and dividend and divide: 3y ÷ -2y.

Do you see we end up with a fraction, -3/2? Well, we don't like fractions in the quotient except as a remainder. So -2y + 5 turns out to be our remainder.

This is what our final answer is going to look like:

2y^2 + 3y + ((-2y + 5)/(3y - 1))

Lesson Summary

Before we end this video, let me review when to use long division and when to use synthetic division. My students really like synthetic division, but it isn't right for every division problem. How do I know the difference?

Any division problem that has a divisor as a one-degree binomial is perfect for synthetic division. This is why we used it on (2x^3 - 14x - 5) ÷ (x + 3). x + 3 is a one-degree binomial with a leading coefficient of 1.

Okay. It's true we can use synthetic division with a divisor that does not have a leading coefficient of 1, but that will give us a fraction. Fractions are messy, and students tend to make more mistakes when using them, so keep to a one-degree binomial with a leading coefficient of 1 and you'll be fine.

Any other division problem needs to be done using long division. This is why we used it on (6y^3 + 7y^2 - 5y + 5) ÷ (3y - 1) and (x^3 - 9) ÷ (x^2 + 3).

One final rule to keep in mind as you do polynomial division: always make sure your polynomials are in descending order - largest exponent to the smallest. If you're missing a term, put a zero to hold that place like we did in example #1.