Brand new technologies don't always catch on right away because they can be expensive and don't always work as well as they should. But once the price comes down and they start to work better it doesn't take very long before it seems like everyone has one. Learn about the numbers behind this, exponential functions!

Review of Types of Graphs

The most fundamental concept of algebra is the idea of using a variable to represent a number, like x. It then moves on to studying the different functions you can make with this letter. But from linear (just x) to quadratic, which is x^2, to higher order polynomials like x^4 or x^10, and even on to rational exponents like x^2/3, most of functions you study all have something in common: the variable is the base, and the exponent is a constant. It's just a number. But this trend ends with the study of exponential functions, where the pattern is reversed and the exponent becomes the variable while the base becomes a constant, and what we end up with is a function that looks like y=b^x. B can be anything, it can be 2, or 6, or 10, or -3, and we just raise it to the x power, so the changing part of our equation is the exponent this time.

Exponential Growth of Cell Phones

So what does this mean? Well, exponential functions are actually seen all the time, so let's take a look at one so you have something to relate it to; cell phones. Well, cell phones were actually invented in the mid-70's, but it wasn't until the early 90's that they really began catching on. And whoo, when they caught on, they blew up! And now it seems like everyone has one, even 8 year olds. So how did that happen?

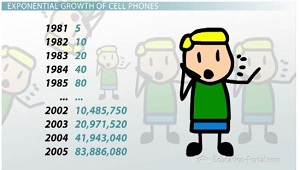Well, I don't really know, but I bet it was something like this. There were probably like 5 people in 1981 that had them (when they looked like bricks and weighed probably as much as a brick, too), but then every year that they got a little smaller and a little faster, and twice as many people got one. That means that in 1982 there were 10, in '83 there were 20, in '84 there were 40 people that had one, in '85 there were 80 - this number keeps on being multiplied by two - and as we go through the years, that number starts getting bigger and bigger. And by 2002, there were 10 million, by 2003 that's 20 million, in '04, 41 million... and really not too long afterward, in 2005, there are 83 million people with cell phones! So what started out in 1981 as only 5 extra cell phones being bought quickly turned in, in '04, 41 million more cell phones being bought, to bring that number all the way up to 83 million. And this is what exponential functions are all about. They start slow and get faster and faster and faster.

Graph of an Exponential Function

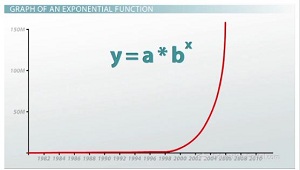Every exponential graph there is will look something like the one we have here, and all exponential equations will be in the form y=ab^x. So what is the equation for this example? Well we started with 5, and then to get to the next number in '82, we just took that 5 and multiplied it by 2. In the next one we just multiplied by 2 again, so that was 5x2x2, and then in the next example we multiplied by 2 again, so that was 5x2x2x2, which we could actually say is 5x2^3, which means the next year was just 5x2^4. And going all the way down to 2005, we came up with our 83 million number by doing 5x2^24. So what we end up with for our equation is just five times two to the something, and let's just use the letter x, 5x2^x, where x represents the number of years since 1981. Basically just tells us how many times to multiply by 2.

Standard Exponential Function

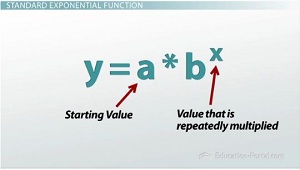This means that in an equation y=ab^x, a is the starting value, while b is the value that is being repeatedly multiplied to that number we started at. For example, a Renaissance painting that costs $100,000 at an auction and then increases by 10% each year would have the equation y=100,000x1.1^x. This is because that painting was initially worth $100,000, and then each year, it increased by 10%, which is essentially saying that it is 110% of what it used to be, and 110% (represented as a decimal by moving it over twice) is 1.1.

We could then go on to answer questions like, 'how much will the painting be worth in 20 years' simply by substituting in 20 for x into our equation. Using order of operations, we do exponents first: 1.1^20 is 6.72749, which basically means that in 20 years, this painting is going to multiply its worth by 6.7 times. We then do 100,000x6.72749, and we find out that after 20 years, this very same painting would now be worth $672,749.

Lesson Summary

To Review:

• An exponential function is one with the variable as the exponent and the base as a constant, and looks like y=ab^x.
• They give you patterns of numbers that are multiplied by the same amount each step of the way.
• In the equation y=ab^x, the a represents where the pattern starts, and the b is what you multiply by each time.
• And finally, the graphs look like curves where they are only increasing by small amounts in the beginning, but grow by more and more each step.