Multiplying and Dividing Rational Expressions: Practice Problems - Answers
The answers are in BOLD below.
NOTE: The transcript from the video is listed below the quiz for your reference.
1.
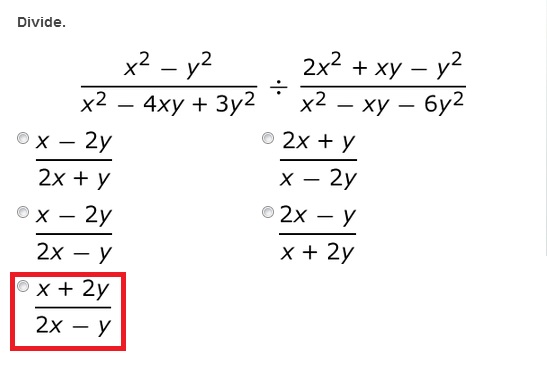
2.
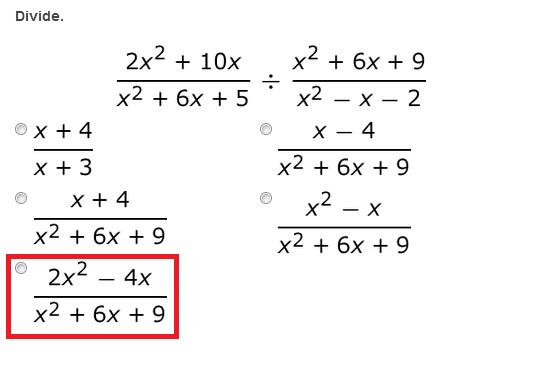
3.
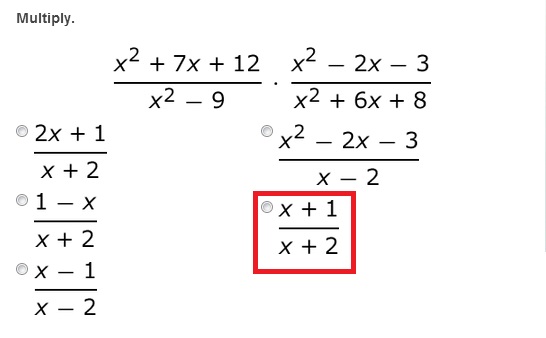
4.
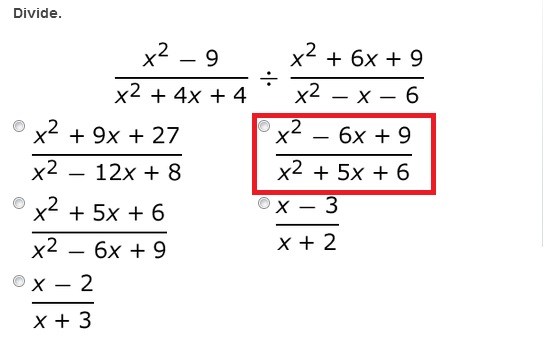
5.

Let's continue looking at multiplying and dividing rational polynomials. In this lesson, we will look at a couple longer problems, while giving you some practice multiplying and dividing.
Review
Multiplication and division of rational polynomial expressions is easy once you remember the steps.
For multiplication: factor, cancel or slash, and multiply.
 |
For division: factor, flip, cancel or slash, and multiply.
 |
Let's do some larger problems.
Example #1
((q^2 - 11q + 24) / (q^2 - 18q + 80)) * ((q^2 - 15q + 50) / (q^2 - 9q + 20))
First, we need to factor. (q^2 - 11q + 24) factors into (q - 8)(q - 3). (q^2 - 18q + 80) factors into (q - 10)(q - 8). (q^2 - 15q + 50) factors into (q - 10)(q - 5). (q^2 - 9q + 20) factors into (q - 5)(q - 4).
So, this is what our new expression is going to look like: ((q - 8)(q - 3) / (q - 10)(q - 8)) * ((q - 10)(q - 5) / (q - 5)(q - 4))
Next, we are going to cancel (what I like to call slash) like terms. We're going to cancel or slash (q - 10) over (q - 10), (q - 8) over (q - 8), and finally (q - 5) over (q - 5).
Now that we have canceled or slashed all of the like terms from the top and bottom, we multiply straight across. Don't multiply anything we slashed because those are now 1's. It turns out, our answer is (q - 3) / (q - 4).
Example #2
((y^2 - 9) / (2y + 1)) / ((3 - y) / (2y^2 + 7y + 3))
Let's factor. (y - 9) = (y - 3)(y + 3) and (2y^2 + 7y + 3) = (2y + 1)(y + 3). Our next step is to flip the second fraction and change it to multiplication. Our new expression is going to look like this: ((y - 3)(y + 3) / (2y + 1)) * ((2y + 1)(y + 3) / ((3 - y)).
The next step is canceling, or what we've been calling slashing. We can slash (2y + 1) over (2y + 1). In the numerator, we have (y - 3)(y + 3) and (y + 3). In the denominator we have (3 - y). If we multiply (3 - y) by -1, we'll get -1(y - 3). Guess what? We can cancel (y - 3) over (y - 3), but remember to leave the -1!
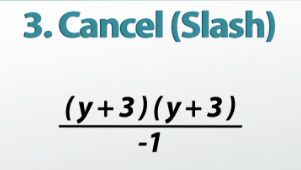 |
So, our final answer's going to look like: (y + 3)(y + 3) / -1.
But hold on a second! Let's multiply the top and the bottom by -1. This is going to give us -1(y + 3) (y + 3) / 1. When we FOIL, we're going to end up with an answer of -1(y^2 + 6y + 9) / 1. Well if we distribute the -1, we end up with (-y^2 - 6y - 9)!
 |
Example #3
((x^2 + x - 2) / (x^2 - 4x - 12)) * ((x^2 - 9x + 8) / (x^2 - 2x + 1)
We begin by factoring. (x^2 + x - 2) factors into (x + 2)(x - 1), (x^2 - 4x - 12) factors into (x - 6)(x + 2), (x^2 - 9x + 8) factors into (x - 8)(x - 1), and x^2 - 2x + 1 factors into (x - 1)(x - 1).
Let's start canceling (or slashing)! We can cancel (x - 1) over (x - 1) and (x + 2) over (x + 2). Once we have canceled, or slashed, all of the terms from the top and bottom, we multiply straight across. That gives us a final answer of (x - 8) / (x - 6).
Lesson Summary
Multiplication and Division of rational polynomial expressions is easy once you remember the steps!
For multiplication: we factor, cancel or slash, and multiply.
For division: we factor, flip, cancel or slash, and multiply.