How to Use Synthetic Division to Divide Polynomials - Answers
The answers are in BOLD below.
NOTE: The transcript from the video is listed below the quiz for your reference.
1.
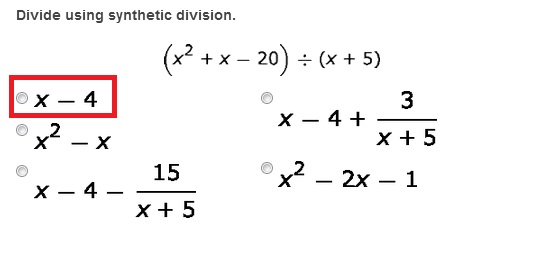
2.

3.

4.

5.

Synthetic division is a 'short-cut' way of dividing a polynomial by a monomial. You still need to know long division, sorry, but this method is way fun when you're dividing by a monomial!
Synthetic Division
Many students prefer synthetic division over long division and even argue why they have to learn long division. You need to know long division because synthetic only works when you are dividing by a first degree binomial, for example, (x + 3). If you are dividing by a longer polynomial, say (x^2 - 2x + 5), you need to use long division!
Example #1: How to Synthetically Divide
(x^2 + 5x + 7) / (x + 2)
At this point, I have seen synthetic division written two ways. The first has the divisor in a half-box on the upper left; the other looks like a division symbol. Both ways are exactly the same, but I prefer the division symbol.
First, if the dividend is not in descending order, we need to do that first. I'll talk about missing parts in the next example. But for now, (x^2 + 5x + 7) is in descending order. The divisor also must be in descending order. And it is: (x + 2).
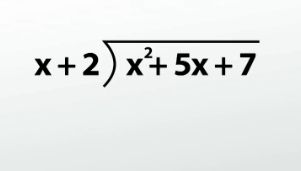 |
Write your usual long division symbol. Place the coefficients of the dividend under the symbol, just like in long division, but do not write the variables. Make sure to leave space between each number. You don't want to get them confused.
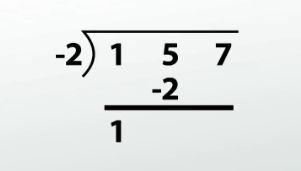
Next, look at x + 2. We're going to write -2 to the left of the long division symbol. You always take the opposite of what you see in the divisor. So inside the long division symbol, we're going to have 1, 5 and 7. On the outside, we're going to have -2.
Our first step is to bring down the leading coefficient, 1.
Multiply 1 * -2, and place the result underneath the next coefficient, 5. So you have -2 * 1, which is -2. 5 + (-2) is 3. (Write that next to the leading coefficient, 1.)
 |
Multiply 3 times -2 and place the result underneath the next coefficient, 7. So -2 * 3 is -6. We add straight down and get 1. (So we have 1 written next to the 3.)
In synthetic division, the degree of the final polynomial answer is one less than the dividend polynomial. Since x^2 + 5x + 7 is degree 2, our answer will be degree 1. What will this look like?
Starting from the left, we'll have 1x + 3 with a remainder of 1. The remainder will be written the same as if we had done this problem as long division - a fraction.
So our answer is going to look like:
x + 3 + 1/(x + 2)
Example #2: Missing Parts
In this example, let's look at a dividend that is missing terms when we write it in descending order.
(x^4 + 81) / (x - 3)
These are both written in descending order, but we don't have an x^3, x^2, or x. In this case, we need to put in a 'place holder' for them. Since we don't have a number, we're going to write 0x^3, 0x^2, and 0x.
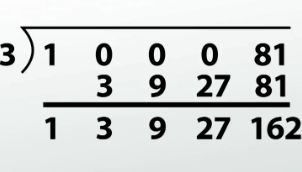
Write the long division symbol. 3 will be our divisor - that's the number that goes in front of the long division symbol. 1, 0, 0, 0, 81 is our dividend. Now, we do synthetic division just like the last one.
We bring down our leading 1.
We multiply 3 * 1, which is 3, and we add down. 0 + 3 = 3, and we do it all over again.
3 * 3 is 9. Add down: 0 + 9 is 9, and do it again.
3 * 9 is 27. 0 + 27 is 27.
Finally, 3 * 27 is 81, and when we add down we get 162.
 |
Now, let's write our final answer. Remember, the answer degree is one less than the dividend polynomial. So our answer is:
x^3 + 3x^2 + 9x + 27 + 162/(x - 3)
Example #3: Larger Problems
(x^4 + 15 x^3 + 58 x^2 - 24 x - 320) / (x + 8)
Place the coefficients of the dividend under the symbol. Next, look at x + 8. We're going to write -8 to the left of the long division symbol. You always take the opposite of what you see in the divisor. Now we're ready for synthetic division.
Our first step is to bring down the leading coefficient, 1.
-8 * 1 is -8. So you have -8 written under 15. Add 15 + (-8), which is 7, and I'm going to write that next to my leading coefficient of 1.
Multiply -8 * 7, which is -56. So we have -56 written under 58. We're going to add down, 58 + (-56), which is 2, and I'm going to write the 2 next to the 7.
Multiply -8 * 2, which is -16. So we have -16 written under the -24. -24 + (-16) is -40, and I write that next to the 2.
Finally, we have -8 * -40, which is 320. I'm going to take -320 + 320, which is 0. It turns out our remainder is going to be 0.
The degree of the final polynomial answer is one less than the dividend polynomial. Since (x^4 + 15 x^3 + 58 x^2 - 24x - 320) is degree 4, our answer is going to be degree 3. What is this going to look like?
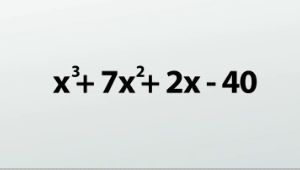 |
So we have (1x^3 + 7x^2 + 2x - 40) with a remainder of 0.
Lesson Summary
Things to remember:
- Make sure your problem is in descending order.
- Create the division by writing only the coefficients.
- Remember, the number that goes outside of the division symbol is the opposite of the original.
- Bring the leading coefficient down.
- Multiply the coefficient by the number outside the division symbol.
- Add that number to the next coefficient until you have no more coefficients to multiply.
- The degree of the final polynomial answer is always one less than the dividend polynomial.
- And don't forget to write the remainder as a fraction!