How to Graph a Complex Number on the Complex Plane - Quiz
Choose your answer and write the correct one down. Then click HERE for the answers to this quiz.
NOTE: The transcript from the video is listed below the quiz for your reference.
1. Which complex number would look like it was at the coordinates (-2,4) if it was graphed?
- -2i+4
- 4-2i
- -2+4i
- 4i-2
- -2i-4
2.
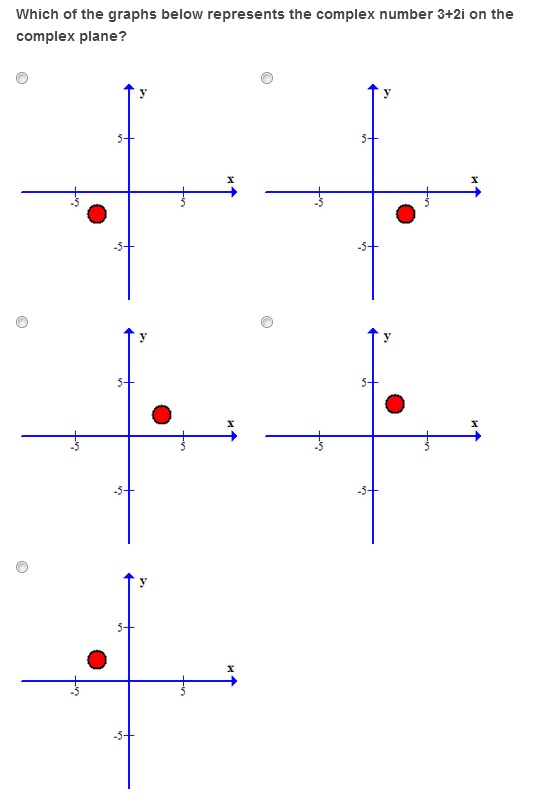
3.
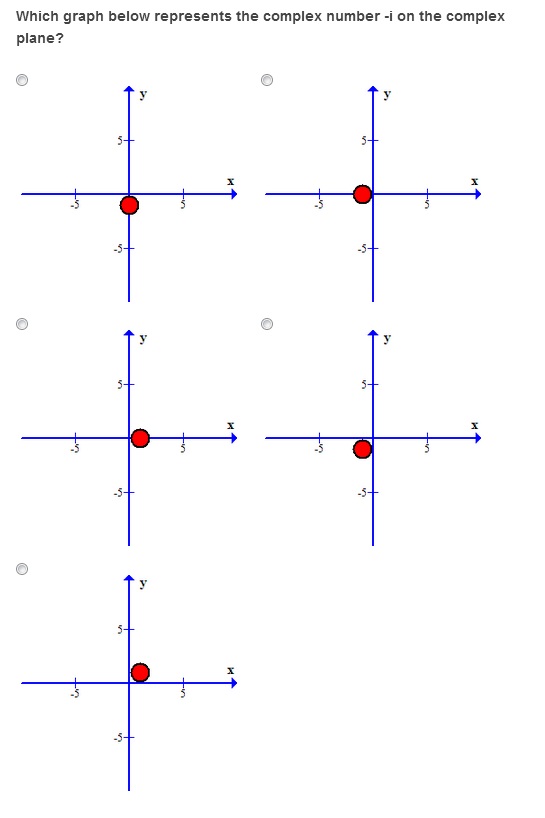
4.
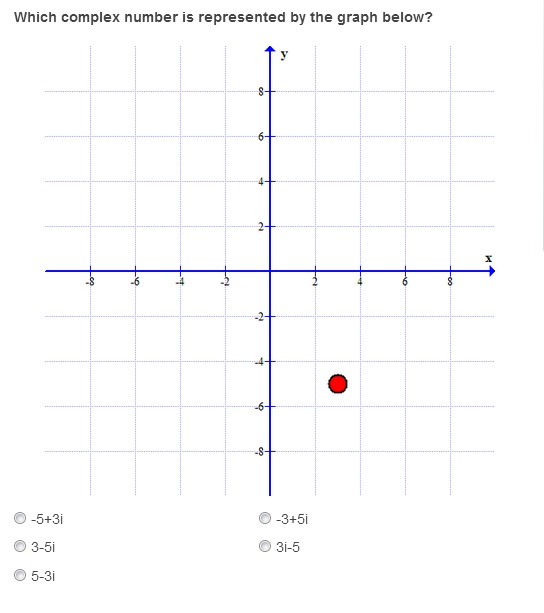
5.
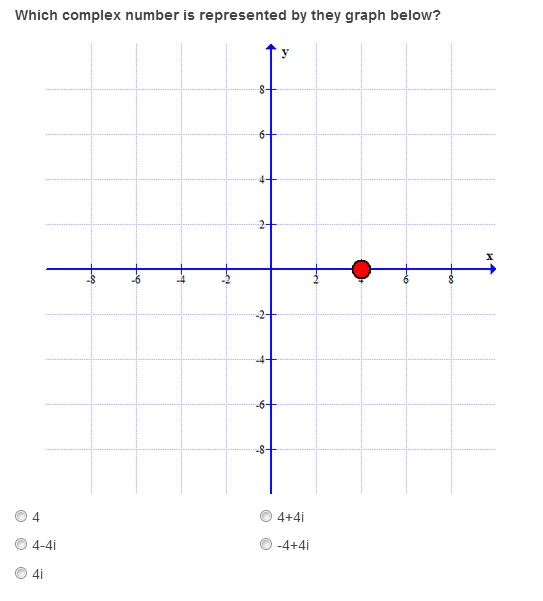
Graphing complex numbers is pretty straight forward, but it's not necessarily intuitive. Check out this lesson to learn the vocabulary and the conventions that you'll need.
Unrelated Numbers
Being a math guy, I was also pretty into my science classes during high school. Naturally, the one that I liked the most was the one with the most math in it - physics. It's now been a while since I've reviewed my physics, but I do remember a few things. One of those things that I remember is that electric circuits are defined by two things - their voltage and their current.
 |
Well, this presented a problem for physicists. They would like to have one number that represents both of these pieces of information, but what one number can represent two things? I suppose they could have used coordinates like (x,y). But what if you wanted to multiply or even divide these two numbers? There's no method for dividing coordinates. Is there a better way?
Graphing Complex Numbers
Aha, complex numbers! Because they have a real part and an imaginary part, they can represent two pieces of information, and we know how to add, subtract, multiply and divide them as well. This makes complex numbers the ideal way to represent two pieces of information in one number.
 |
But to make complex numbers better than coordinates in every way, we'll need to be able to graph them as well. Because there are two pieces of information in each complex number, we can put this info into a two variable graph. This time, instead of having an x-axis and y-axis, we'll have a real axis and imaginary axis. But even though the axis will be a little different, the process of putting the numbers on the graph is, essentially, the same.
Let's take a look at an example:
Graph -2 + 5i
The axes will still look the same, but now our x-axis is, instead, going to be the real part of the complex number, so we call it the real axis. That makes the y-axis our imaginary axis and will represent the imaginary part of the number. That makes graphing -2 + 5i, basically, the same as graphing (-2,5) on a normal x/y-axis. We go over to -2 on the real axis, and up to positive 5 on the imaginary one, giving us a point right here.
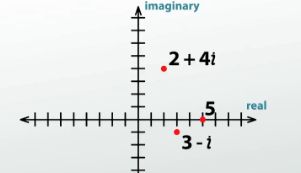 |
That's all there is to graphing complex numbers! Any complex number will simply look like a point. 3 - i would be a point at (3,-1), like this. 2 + 4i would be up here. 5 would be a point at (5,0), like this. That means that any point on the x-axis, (or really what is the real axis) is a complex number without any imaginary value. It's not a stretch to then say that any point on the y-axis (or the imaginary axis) is a complex number without a real value. That makes the point shown right here, just -3i. When it comes to graphing complex numbers, that's it!
Lesson Summary
Because complex numbers have two parts, they are great for representing topics that have two pieces of information. When graphing complex numbers, the x/y-axis becomes the real/imaginary axis. All complex numbers will look like points on a graph.