How to Divide Complex Numbers - Quiz
Choose your answer and write the correct one down. Then click HERE for the answers to this quiz.
NOTE: The transcript from the video is listed below the quiz for your reference.
1.
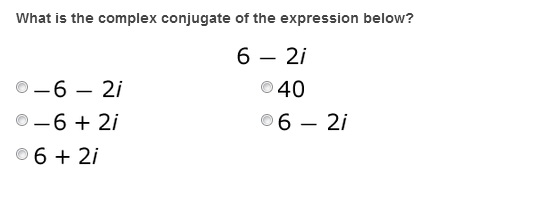
2.
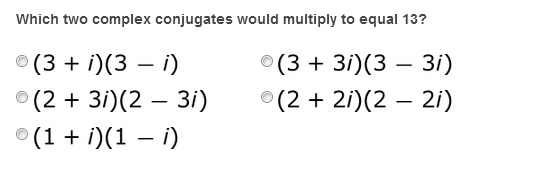
3.

4.
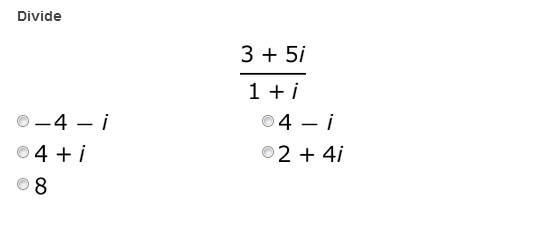
5.
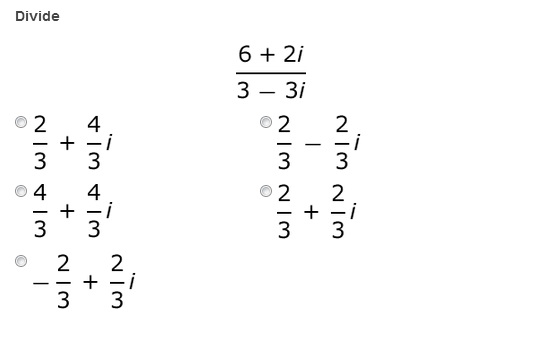
While adding, subtracting and multiplying complex numbers is pretty straightforward, dividing them can be pretty tricky. It comes down to the process of multiplying by the complex conjugate. Learn about what that is, and how to do it, here.
Complex Numbers
Complex numbers are a combination of a real number with an imaginary one. Because of that, we can express them generally as a + bi, where a is the real part of the number and b is the imaginary part. As long as you remember that i^2 = -1, then adding, subtracting and multiplying them is really just a review of combining like terms and multiplying binomials with FOIL. But when it comes to dividing complex numbers, some new skills are going to need to be learned.
 |
Complex Conjugates
 |
Along with these new skills, you're going to need to remind yourself what a complex conjugate is. If you haven't heard of this before, don't worry; it's pretty straightforward. A conjugate is a binomial where the sign on the second term has been switched. So the complex conjugate to a + bi is just a - bi, and visa versa. Here are some examples of complex conjugates: 2 + 3i and 2 - 3i, or -3 - i and -3 + i or 4 - 5i and 4 + 5i. Just remember that the sign on the first term stays the same, but the sign on the second one switches.
Multiplying Conjugates
Conjugates are special because there is a pattern to multiplying them. Let's show this with two of our examples from above: 2 + 3i and 2 - 3i. Multiplying these two complex numbers with FOIL will give us 4 - 6i + 6i - 9i^2. But then when we combine like terms, the two groups of i's in the middle are going to cancel out. Substituting in -1 for i^2, and then doing 4 + 9 gives us our answer as 13, a real number!
Multiplying any two conjugates will make these middle terms cancel out. Which means that multiplying two complex conjugates will always make the i's cancel out, leaving us with a real number every time: (a + bi)(a - bi) = a^2 + b^2. Okay, so why do I bring this up? Well, dividing complex numbers will take advantage of this trick.
Dividing Complex Numbers
There really isn't a good way to figure out how many of these complex numbers fit into that one, so instead we do some fancy hand waving (using the conjugate) to make the imaginary part of the complex number we're diving by go away. Then it's just dividing by a real number, something that we know how to do.
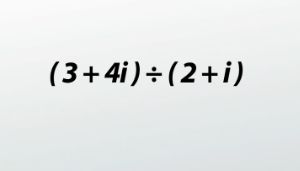 |
Whew, that's a lot of words; let me show you what I mean. Take the example (3 + 4i) / (2 + i). Like I said earlier, I have no idea how many 2 + is fit into 3 + 4i, so writing the problem this way doesn't really give us much. Instead, changing it into a fraction will allow us to begin using our fancy math tricks. If we now remember what we just learned about the complex conjugate, we can change this from dividing by a complex number (something we don't know how to do) into dividing by a real number (something we do know how to do). So we want to multiply the denominator by its conjugate, 2 - i (that would make it a real number), but we can't just do anything we want. We have to leave the problem the same. Multiplying by some random number will change it, but multiplying by 1 is actually not going to change it at all.
Because of this, our next step to this problem will be to multiply our fraction by (2 - i)/(2 - i). This is kinda like multiplying a fraction by 4/4 to get a common denominator, just with more 'complex' numbers, eh? Get it? Sorry for the nerdy joke. Anyways, we're multiplying by (2 - i)/(2 - i). This means we have to FOIL out the top and the bottom. This means multiplying the first, outside, inside and last terms, substituting in -1 for i^2, and combining like terms leaves us with this: (10 + 5i)/5. Since this answer has real numbers and imaginary ones, we'd like to split it up and write it in the standard complex form. This means splitting our answer up into 10/5 + 5i/5. While this won't always be the case, it is true this time we can take our answer one step further and simplify both fractions as well. 10/5 is 2, and 5/5 is 1, so our final solution is 2 + i.
 |
Let's run through another example just to get a look at a problem that might not have numbers that work out so nicely. I'll highlight the process to give you a review of the sequence but skip through the specific operations to save you some time. If you find yourself getting lost, either pause the video and check my math, or maybe check out a previous video to brush up on your skills. Alright lets do it: (4 - i)/(2 - 3i).
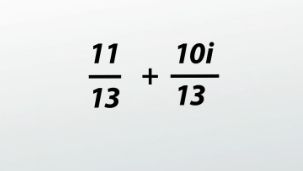
The first part of this problem is that we want to get the imaginary part of the complex number out of the denominator. To do that, we'll need to multiply it by the complex conjugate. That means taking 2 - 3i and changing it to 2 + 3i. But since we can't change what the fraction is, we need to multiply the numerator and the denominator by the same thing, (2 + 3i)/(2 + 3i). This is the main conceptual idea of this whole problem. Now we multiply the two complex numbers in the numerator, (4 - i) and (2 + 3i) with FOIL; we multiply the two numbers in the denominator with FOIL, (2 - 3i) * (2 + 3i), and we get this: (8 + 12i - 2i - 3i^2)/(4 + 6i - 6i - 9i^2). Combining like terms will lead us here: (8 + 10i - 3i ^2)/4 - 9i^2). Then substituting in -1 for i^2 gets us to this: (8 + 10i - 3(-1))/(4 - 9(-1)). Combining like terms one more time gets us to this: (11 + 10i)/13. And then because there are real and imaginary terms in our answer, we split up the fraction into two new ones to put it into general complex form. This leaves us with 11/13 + (10/13)i, and we're done because the fractions are as simple as they can be. While there are a lot of fancy math tricks in these types of problems, hopefully you're starting to get a feel for it and can handle the quiz questions following this lesson.
 |
Lesson Summary
Let's review. Conjugates are two binomials with everything the same except the sign on the second term. This makes the complex conjugate of a + bi, a - bi. We take advantage of these conjugates when we divide complex numbers. In order to do this, we end up having to multiply the top and the bottom of the fraction by the complex conjugate of the denominator. This ends up changing the denominator into a real number, which then allows us to split up the fraction into a