How to Add, Subtract and Multiply Complex Numbers - Quiz
Choose your answer and write the correct one down. Then click HERE for the answers to this quiz.
NOTE: The transcript from the video is listed below the quiz for your reference.
1. Which basic operation of complex numbers will require you to learn completely new skills?
- Division
- Addition
- Subtraction
- Multiplication
- None of the above
2.
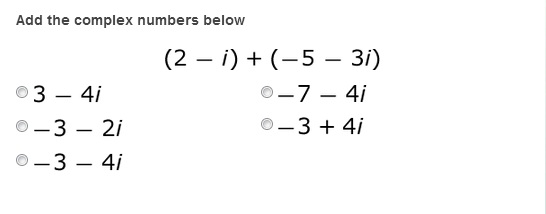
3.

4.
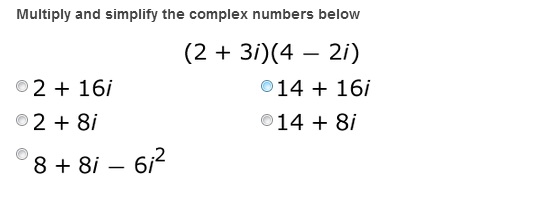
5.
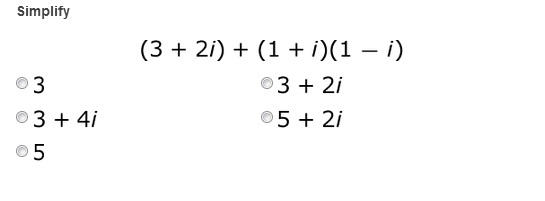
Knowing that complex numbers exist is the first step. But that knowledge alone won't help you do much with them. Learn the basics of complex number addition, subtraction and multiplication here!
Imaginary and Complex Numbers
Imaginary and complex numbers might be the most abstract topic you'll be exposed to in an algebra class. Because they don't actually exist and you just need to imagine that they do, a lot of students struggle with them. But if you can let go and accept that we can still do math with them, it turns out that there isn't anything too tricky about working with them.
 |
But before we get into that, let's quickly review what a complex number is. Any time we take the square root of a negative number, we get an imaginary number. When this happens, we use i to represent the square root of negative 1. This means that i^2 is just regular old -1. It turns back into a real number!
When we take an imaginary number and add a real number to it, we end up with a complex number often denoted by a+bi, where a represents the real and b the imaginary portion of the number.
Okay, so how do we do the basic operations on these numbers? This is where it gets nice. Although division will require you to learn a new skill, addition, subtraction and multiplication of complex numbers will all come down to things you already know how to do. As long as you can combine like terms or multiply binomials with FOIL, you're good to go!
Adding Complex Numbers
 |
What do I mean? Well, for example, adding the two complex numbers (3 - 2i) and (-5 - 4i) is as easy as adding 3 and -5 to get -2, then -2i and -4i to get -6i. This makes our answer -2 - 6i. That's it!
You wouldn't even really have to know that we're adding complex numbers to do this problem. It's all just combining like terms. First combine the real parts, then the imaginary parts, and you're done.
If you like keeping it simple and just thinking about it this way, that's cool. But the formula for adding complex numbers is basically another way of writing what I just said, but with math instead of words. Adding the complex numbers a+bi and c+di gives us an answer of (a+c)+(b+d)i.
 |
Subtracting Complex Numbers
Subtraction is basically the same, but it does require you to be careful with your negative signs. Let's try the example (-2 + 4i) - (3 - i). Combining the real parts looks like -2 - 3=-5, while the negatives will make the imaginary parts a little bit trickier. The first imaginary term 4i minus the second one -i gives us 5i for our imaginary term. Remember that subtracting a negative turns into adding a positive. Therefore our answer is -5+5i.
If you prefer, the formula for subtraction of complex numbers looks like this: (a+bi) - (c+di)=(a - c)+(b - d)i.
Multiplying Complex Numbers
On to multiplication. This will again rely upon an older skill, the multiplication of binomials. Whether you use FOIL, the area method, the distributive property or one of the other many ways to do it, this is the process of multiplying two terms like (x - 5)(x+2).
Now, though, we are simply doing the same thing, but with is instead of xs. Take (3+2i)(4 - i) as an example. I'll go ahead and use FOIL because it seems to be the most common method, but any way you would like to do this is totally fine.
 |
Multiplying the first terms (3 * 4) gives us 12. The outsides will be 3 * -i, giving us -3i. The insides will be 2i * 4, which turns into 8i, and finally the last terms (2i * -i) becomes -2i^2.
We can then again use our combining-like-terms skills to simplify our expression down to 12+5i-2i^2. If you said you were done, you'd more or less be right, but you'd be forgetting one step that would prevent your answer from being completely simplified. This step requires you to remember that i^2 is just plain old -1! No more imaginary numbers. Substituting this in for i^2 into our expression and then again combining like terms gives us our final answer as 14+5i.
Let's do one last example that ties all these skills together. Simplify (-7+14i) - (3+2i)(1+4i).
Order of operations tells us to do multiplication before subtraction, so we can FOIL out the first two complex numbers first. Multiplying the firsts, outsides, insides and lasts gives us (3+12i+2i+8i^2). In order to not forget, let's substitute -1 in for i^2 right away and then combine both the real and imaginary parts at once to give us -5+14i.
We can now move on to the subtraction part of this problem. It again comes down to just combining like terms. First, the real parts: (-7-(-5)). Again, subtracting a negative is just like adding a positive, so we just get -2. Then the imaginary parts: (14i - 14i) is just 0. That means our answer is simply -2!
This example illustrates why it's good to be able to use complex numbers. If you let yourself imagine that they exist, you might just end up with a number that truly does!
Lesson Summary
 |
To review, adding and subtracting complex numbers is simply a matter of combining like terms. You combine the real and imaginary parts separately, and you can use the formulas if you like. Multiplying complex numbers is basically just a review of multiplying binomials. The only extra step at the end is to remember that i^2 equals -1. Dividing complex numbers, on the other hand, is a little more complicated and will be taught in a later lesson.