How to Evaluate Absolute Value Expressions - Answers
The answers are in BOLD below.
NOTE: The transcript from the video is listed below the quiz for your reference.
1. Which statement is not TRUE about absolute values?
- A number directly in front of an absolute value implies multiplication
- They are treated similar to parenthesis
- They change subtraction symbols within them into addition
- Substituting values into absolute value is no different than other algebraic expressions
- They make the end result a positive number
2. If a question requires us to know the value of y-x, but all we know is that x+2=y, what can we do?
- There is nothing we can do
- Subtract x from both sides of the equation
- Add y to both sides of the equation
- Add x to both sides of the equation
- Subtract 2 from both sides of the equation
3. If a question requires us to know the value of 2x+y, but all we know is is that x+y=5, what can we do?
- Subtract 5 from both sides of the equation
- Add x to both sides of the equation
- Subtract y from both sides of the equation
- Multiply both sides of the equation by 2
- There is nothing we can do
4. Evaluate |r+4|-3|s| when r=5 and s=-1.
- Not enough information
- -6
- 12
- 6
- -12
5. Evaluate |r+s|-(r+s) when -s=r+8
- Not enough information
- -8
- 8
- 0
- 16
Substituting values into absolute values doesn't have to be too hard, but it can be if you're given deceiving beginning information. See if you're up to it by checking out this video!
Solving by Substituting Variables
So we know that absolute values make things positive, but how does that effect how we evaluate absolute values at specific values? Let's take a look at an example:
Evaluate m|5-2n|+7, when m equals -2 and n equals 10. This problem is actually no more different than any other problem that asks us to substitute in values as long as we don't fall into the biggest absolute value pitfall; the absolute value bars DO NOT change subtraction symbols into addition ones. Yes, they do make things positive, but only after you've completed whatever operations are going on on the inside.
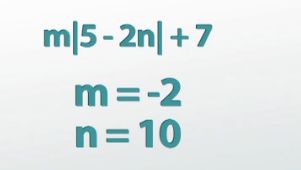 |
So if we first substitute in -2 for m and 10 for n, we treat the absolute value bars like parentheses and we begin on the inside of them. Multiplication comes before subtraction, so I do 2*10 and I get 20. Then I do 5-20 and end up with -15, and only at that point, after I've finished all the different things on the inside of the absolute value, do we actually take the absolute value, making -15 positive 15. Again, because absolute value bars are kind of like parentheses, when you have a number in front it means multiplication, and -2*15 is -30. Last but not least, -30+7 is -23.
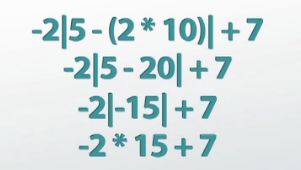 |
Solving by Replacing Groups of Variables
Now, where these problems can get kind of tricky is when the values of m and n aren't given to us quite so nicely. Take this example:
Evaluate |2m-2n| + |n-m| when m-n is equal to 4. So instead of simply telling us what n and m are individually, it only gives us what their difference is. It's going to be up to us to manipulate the given equation to make it look like what we want.
So what do we want? Well, the two expressions that would be nice to be able to substitute in are 2m-2n (that first absolute value) and n-m (that second one). If we knew both of those, we could simply plug in the numbers that we knew and be two steps away from our answer.
This means that it's up to us to learn what 2m-2n and n-m are from only the info we've got, which is m-n is 4.
So we need to turn m-n into 2m-2n. Luckily, we know that equations can be manipulated by doing the same thing to both sides to give us equivalent statements. So all I really need to do here is multiply everything in this equation by 2 because I want to turn m into 2m and I want to turn -1n into -2n. So multiplying the whole thing by 2 and distributing in gives us that 2m-2n is equal to 8. And we've already got one of our two expressions.
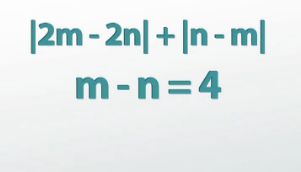 |
The other thing we need to do is make m-n into n-m; we need to switch the order around. This basically means I want to make the positive m into a negative one and make the negative n into a positive n. Again, I can manipulate equations by doing the same thing to everything, so if I just multiply everything by -1 and distribute it out, my given information turns into -m+n equals -4. Because addition can be written in either order as long as the sign stays with the value, that's the same thing as n-m is equal to -4. We've found our second expression.
Now that we've changed our given information into what we really want, all I have to do is substitute in the two new equations we came up with. So I now know that 2m-2n is 8 so I can substitute that in for the first part of my absolute value in the original question; I know that n-m is now -4 so I can now substitute that in. What I end up with is just |8| + |-4|. Absolute values leave positive numbers alone so the 8 stays the same; they turn negative numbers positive so the -4 becomes positive, and 8+4 is 12.
Lesson Summary
To review, absolute value signs do not change addition to subtraction, they just make the end value positive. You have to do whatever operations are on the inside of the absolute value and then make it positive in the end if you have to.
Substituting values into absolute value expressions is no different than any other algebraic expression. When the given information is not exactly what we need, we can manipulate it to become what we do need.