How to Take a Determinant of a Matrix - Quiz
Choose your answer and write the correct one down. Then click HERE for the answers to this quiz.
NOTE: The transcript from the video is listed below the quiz for your reference.
1. Which choice below could be a possible answer to the determinant of a matrix?
- M
- y=-1
- x=6
- (5,10)
- -9
2.
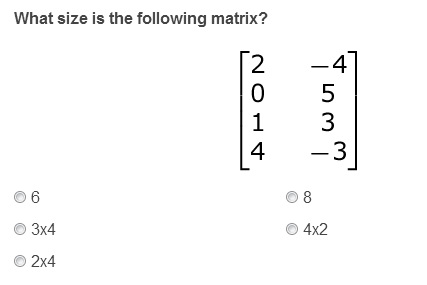
3. Which of the following would be a square matrix?
- 9x3
- 1x10
- 6x6
- 6x5
- 5x6
4.
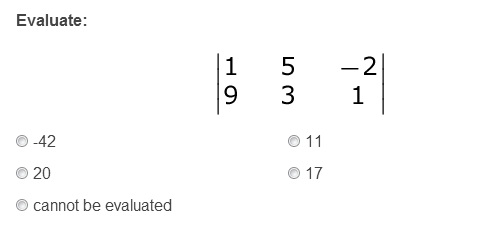
5.
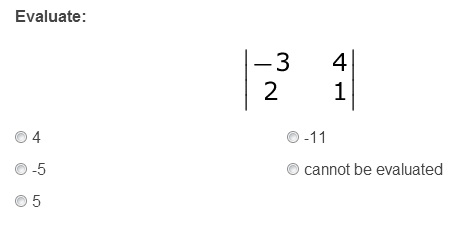
Matrices are incredibly powerful and can help you do all sorts of things, but one of the most basic (and surprisingly helpful) operations you can perform on one is to take its determinant. Learn how to do that here!
What's a Matrix?
One of the simplest, most unique operations you can perform with a matrix is called the determinant. In this video, we're going to concentrate on what it looks like and how you calculate it. We're not going to go too in depth but a little matrix basics and vocabulary is needed for us to this.
 |
Matrices are grids of numbers that are surrounded by brackets, a kind of squared-off parentheses. And matrices are labeled by their number of rows and columns, so we call a matrix an M x N matrix, where M is the number of rows and N is the number of columns. What you see here is a 3 by 5 (3 x 5) matrix, because it has 3 rows and 5 columns of numbers which is a total of 15 numbers inside. This would be a 6 by 1 (6 x 1) matrix because of its 6 rows and only 1 column. Both of these examples look like rectangles because the number of rows and columns are different.
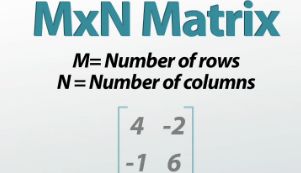 |
Square Matrices
When the number of rows and columns are the same, we end up with a square matrix. That means that we could have a square matrix that is 1x1 or 2x2 or 3X3. Because they have the same number of rows and columns, the mathematical way of defining a square matrix is to say that it is any matrix that is N x N.
The reason we need to know what a square matrix is, is that a determinant can only be calculated on square matrices. As long as it is a square matrix, the determinant of any matrix is simply a number, so the determinant takes a matrix and boils it down to one value. Actually calculating the determinant gets more and more difficult as the matrix gets bigger and bigger, so we'll start by looking at the smallest square matrix (1x1) and practice on bigger and bigger ones.
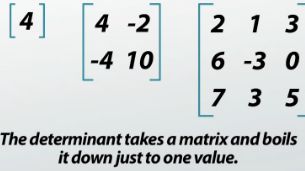 |
Taking the determinant of a 1x1 matrix is what mathematicians call 'trivial.' This is because there is essentially nothing to do. For example, the determinant of the matrix (which is denoted by the straight bars instead of the brackets) |4| is just 4. Or the determinant of the matrix |-5| is just -5. Notice that the matrix is no longer in brackets but just in straight, up-and-down bars, kind of like absolute value signs. Although the | | symbols look the same as an absolute value, this is just a coincidence and probably comes down to the fact that mathematicians are lazy and don't want to draw anything else more complicated.
2X2 Matrix
Taking the determinant of a 2x2 matrix starts to get a little more complicated. Let's look at the example |5 4 , 8 2|. Again, because the matrix is surrounded by | | we know that we are being asked to calculate the numeric value of the determinant. Now, we have to start with a process that involves multiplying the diagonals and subtracting the products. We start with the top left to bottom right diagonal; in this example, we would do (5)(2). We subtract the bottom left to top right diagonal, which is (8)(4) from that. What we end up with is 10 - 32 = -22, so the determinant of this matrix is simply -22.
Another quick example might be |-1 5 , -4 3|. Here we would do (-1)(3) - (-4)(5). Be careful when you subtract a negative, since it changes sign. So, (-1)(3)-(-4)(5) = -3 + 20 = 17.
Looking at a generic matrix with variables as entries instead of numbers ( |a b , c d| ) gives us the formula for the determinant of a 2x2 matrix as ad - bc, which again we get from multiplying the diagonal top left bottom right and subtracting the diagonal bottom left top right.
Bigger Matrices
Once we get to matrices bigger than 2x2 we end up having to calculate a bunch of smaller determinants in a row in order to calculate the main determinant.. This skill is not essential for this class, and so we'll just go through one quickly so you can be exposed to it, but don't worry about memorizing the process.
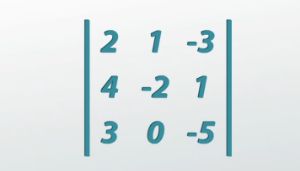 |
For example, if we wanted to calculate the determinant of this 3X3 matrix right here, we would have to do 2 multiplied by the 2X2 matrix determinant that you get when you cover up the row and column that 2 is in. Now, we would take away 1 multiplied by the 2X2 matrix determinant that you get when you cover up the row and column that 1 is in. Finally, -3 times the determinant that you get when you cover up the row and column that -3 is in. Now, it becomes a process of evaluating the determinants of these smaller 2X2 determinants with the formula that we just learned, which is ad - bc. In this case, we'd end up with determinant of this 3X3 matrix being 25. If we were to take the determinant of a 4X4 or 5X5 or 10X10 or 50X50, it gets more and more complex, but it's essentially the same process all over again. You keep taking smaller and smaller determinants until you get down to 2X2 determinants, where you can actually start calculating the values.
 |
Lesson Summary
- Matrices are labeled by # rows X # columns and are often denoted as MXN.
- A matrix with the same number of rows and columns is called a square matrix
- Any square matrix has a determinant, which is a single number value associated with the matrix.
- The determinant of a 1x1 matrix is simply the only number in the matrix.
- The determinant of a 2x2 matrix is ad - bc.
- The determinants of bigger matrices can be calculated by breaking it down into a bunch of smaller 2X2 matrices.
- What look like absolute value bars | | are put on the outside of the determinant in order to indicate that we're being asked to calculate the determinant.