Math 101: College Algebra

As math gets more and more complicated and there become more and more numbers flying around, it becomes really handy to put all these numbers in a nice organized grid... hello matricies! Learn about what they are and why there are used.

What is a Matrix?

Matrices are the main ingredient of a branch of mathematics called linear algebra. Linear algebra first becomes nice when you begin solving systems of linear equations. By only putting the essential information into a big chart, it allows you to focus on the numbers and you can simplify a lot of the process.

Definition of matrix

For example, let's say you're solving a system of two equations with two variables. You can solve this with elimination by multiplying the top equation by 3 and the bottom equation by 2. This makes the coefficients on your xs opposite, and you can add them together to eliminate the xs and just get the ys by themselves and go from there by solving for y and solving the system.

So that's not too bad, but let's say that instead of having two equations and two variables, we had seven equations and seven variables. This gets way messier! I have xs, ys, zs, ws, as, bs and cs, and if I wanted to try to solve this, it would be a huge headache writing out all those different letters every single time.

Parts of the Matrix

But if we instead take out all the letters and just put it into one big chart, we can kind of cut down on a lot of the work we have to do. We put this chart of numbers in what we call brackets. They're kind of like squared off parentheses. And it's organized into rows and columns. Each row represents one of the original equations from our problem, and each column represents all the different coefficients (numbers in front of the variables) that were on a particular variable. So all the numbers in the first column are all the different coefficients that were in front of the xs, for example.

You can add coefficients to eliminate the x.

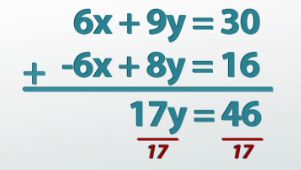We can still do the same type of thing. We can still use the elimination method and multiply the whole top equation by 2, which then turns my whole new matrix into this. And again, we can still add rows together in order to eliminate variables. Adding this top row to this second row eliminates my xs.

As you can see, this process can still take a pretty long time, so a matrix doesn't necessarily make it easy, but it makes it easier. It also allows us to tell a computer how to do this, and so matrices and linear algebra come up in computer programming a lot because it's really easy to tell the computer what this big grid of numbers is and then the computer can do the whole process for you in a few seconds.

Adding and Subtracting Matrices

So once we start becoming used to dealing with these grids of numbers, we can start to do more and more complex things with them. We can add them together as long as the number of rows and the number of columns are the same, we can add two matrices by simply adding the numbers that are in the same spots. I can add the 2 and the 4 together because they are in the top left, and I get my new top left number as 6. I can add the top right numbers (-3 and -2) together and get -5. I can add all the individual entries up and end up with my new matrix.

Adding and subtracting matrices

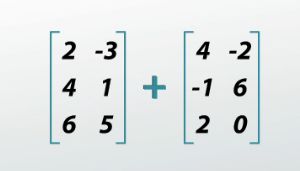I can do subtraction in exactly the same way. Again, we just subtract the numbers that are in the corresponding spots, and as long as the matrices have the same numbers of rows and columns, we end up with a new matrix that looks the exact same size.

Multiplying Matrices

We can even multiply matrices. This is where it starts to get more complicated. The number of columns in the first matrix needs to be the same as the number of rows in the second matrix. It's a process of multiplying the first row in the first matrix with the first column in the second matrix, one entry at a time, and then adding the resulting products up into one entry. The top left entry of my end matrix would be 5.

Multiplying matrices

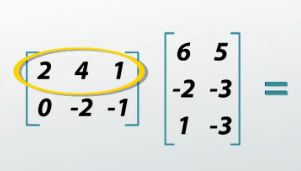I can do that again with the first row in the first matrix with the second column in the second matrix; 2*5 + 4*-3 + 1*-3 ends up with a -5 in the top right corner. I continue this process for each row in the first matrix with each column in the second matrix, and I end up with this resulting matrix, which isn't the same size, but it has the number of rows from the first with the number of columns from the second, and we get this.

Lesson Summary

So to review, matrices are grids of numbers divided into rows and columns and put into brackets. They are the center of a whole branch of mathematics called linear algebra. Most simply, they're used to solve systems of equations with a lot of variables, but they quickly become more complex and end up being useful in all sorts of fields.