If you're not satisfied with knowing how many views your YouTube video will get any one day and need to know how many total views you're getting, geometric series are for you! Learn more in this lesson.

How Many Views Will We Get?

In a previous lesson about geometric sequences, we saw that if a YouTube video gets two hits on the first day, but then three times as many new hits each consecutive day, it would quickly be getting over 3,000,000 new hits 14 after it was posted. But this only helped us figure out how many new hits it got each specific day. If we want to know, for example, how many total views it got in those first two weeks, we'd have to add all those entries up.

How many new views will the video get each day?

That's when the geometric sequence turns into a geometric series. Of course, we could try to add these numbers up by hand. But, as is probably obvious by now, mathematicians love shortcuts. What we're trying to do is add up a geometric sequence.

Proving the Formula

A geometric sequence starts with some number. Let's call it a_1. Then, we want to add the next term, which would be a_1 * r, because we just keep on multiplying. The next one would be a_1 * r^2, then a_1 * r^3, and we go on and on until the nth term, which is a_1 * r^(n - 1). Because it's a series, we want to add all of these things, so we're adding them all up.

Let's say that this is equal to s, our sum. This is what we've got. This is what we want to know. What is s equal to? Well, if s is equal to what we've just written there, I could multiply both sides of the equation by r. That would mean r * s. Now I just have to distribute an r to everything in there. a_1 turns into a_1 * r, the a_1 * r turns into a_1 * r^2, the a_1 * r^2 turns into a_1 * r^3 and so on. The a_1 * r^(n - 1) would turn into a_1 * r^n. That would be my last term.

The reason I did that is because we can actually use a trick now. I take the two left-hand sides of the equation, s and r * s, and I subtract those, so s - (r * s). I then take the right-hand sides of the equation and subtract them: a_1 + (a_1 * r) + (a_1 * r^2) and all that stuff minus (a_1 * r) + (a_1 * r^2) + (a_1 * r^3) and all that stuff.

This is the sum for any finite geometric series.

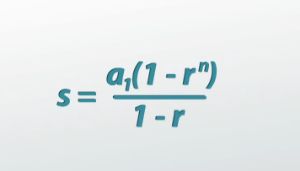Most of these things are going to cancel. The a_1 in front on the first one will stay. But then a_1 * r and a_1 * r cancel, a_1 * r^2 and a_1 * r^2 cancel, all these things cancel. The a_1 * r^(n - 1) cancel. But then I do have, on the other one, the a_1 * r^n, which doesn't cancel, so I have a negative a_1 * r^n.

A lot of that stuff goes away and all I'm left with is s - rs = a_1 - (a_1)(r^n). Now, because both sides of this equation share a factor, I can factor out an s from the left-hand side to get s(1 - r). I can factor out an a_1 from the right-hand side to get (a_1)(1 - r^n).

Then, on the left, because I'm going to try to get s by itself, I can undo the times (1 - r) with divide by (1 - r). What I get is that s is equal to (a_1)((1 - r^n)/(1 - r)).

That was some pretty fancy math, but what we have come up with is the sum for any finite geometric series. So, if we're taking the sum, from the first term to the nth term, of the geometric sequence (a_1)(r^(n - 1)), that is simply equal to (a_1)((1 - r^n)/(1 - r)). What we now have is our formula. Now, armed with our formula, we can actually answer the question of how many total views our video got in the first two weeks.

Solving the Formula

We decided that the rule for nth term was 2 * 3^(n - 1), because 2 was the first term and the common ratio was 3; we kept on multiplying by 3 each time. This means that if we want to know how many total views we got in the first two weeks, we're taking the sum of that exact rule from day 1 through day 14.

Now I can just plug numbers into the formula. a_1 is 2. In this case, n is 14 because we're going through 14 days. r is 3.

I get 2((1 - 3^14)/(1 - 3)). This simplifies down into 2((1 - 4,782,969)/(1 - 3)). Keeping on and subtracting, I get 2(-4,782,969/-2). Doing the division, negative divided by negative is a positive. Then, doing the multiplying, and it looks like our video got 4,782,968 views in the first two weeks alone.

Simplifying the formula

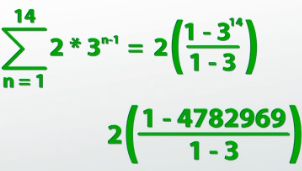Finding for Formula for an Infinite Series

The formula we came up with works for all finite geometric series. But, as it turns out, it's also going to work for some infinite geometric series as well. If r, the common ratio, is bigger than 1, then the series just gets bigger and bigger and bigger, and it's never going to stop. Finding a specific sum is going to be impossible because it's just going to become infinity.

If, instead, r is in between 0 and 1, the sum is going to converge to a specific number. This is because the numbers that we're going to be adding on get so small that they basically turn into 0 and don't really do anything.

So, our sum, from 1 to infinity, of our geometric series doesn't have the same equation, (a_1)((1 - r^n)/(1 - r)). Now, that r^n in the old formula might be (1/2)^100, because we're going to infinity, so the n is going to get huge. And (1/2)^100 is like 0.00000… I don't even know; there's a ton of 0's there.

This means that if we kept going, (1/2)^200, (1/2)^300, it just gets smaller and smaller. So, 1/2 to the infinity is going to turn into 0, which means that this r^n disappears from our formula and our formula turns in (a_1)((1 - 0)/(1 - r)). I can then multiply the a_1 to the 1 and my formula simplifies down to (a_1)/(1 - r).

The sum converges to a specific number.

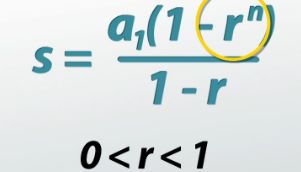Solving an Infinite Geometric Series

One of the classic examples of an infinite geometric sequence that actually has a finite sum has to do with a ball being shot up into the air and then it bounces over and over again until it basically stops bouncing and lands on the ground. The question is: how far did the ball travel?

Let's say that, in this example, it was shot up into the air and came back down and travelled 2 feet in its first trip. Then, when it bounced and hit the ground, it travelled 1/4 of the distance. So if it went up and down 2 feet the first time, the second time it would only go up and down half a foot. Then, it would only go up and down .125 feet and then it would continually bounce smaller and smaller amounts. It would go, theoretically, forever, to infinity.

The rule for this sequence would be a_n = 2 * (.25)^(n - 1). 2 is the beginning value and the common ratio is 1/4.

We want to take the sum, from the first through the infinite term of that rule, and now I can just use my formula: (a_1)/(1 - r). a_1 is 2 and r is 1/4. My formula turns into 2/(1 - 1/4). 1 - 1/4 is 3/4. Dividing by a fraction is the same thing as multiplying by its reciprocal. I get 2 * 4/3. Putting a 1 under the 2 and multiplying across gives me 8/3, or around 2.6667 feet.

Lesson Summary

To review, finite geometric series can be evaluated with the formula (a_1)((1 - r^n)/(1 - r)) where r is the common ratio and n is the number of terms in the series. Infinite geometric series can be evaluated using a simplified version of this formula, (a_1)/(1 - r), but only if r is in between 0 and 1.