Math 101: College Algebra

Learn all of the different types of numbers: natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers. This free video lesson teaches you how to classify any numbers you come across.

Natural Numbers

This is a lesson on the different classifications of numbers, which is basically a big word for just saying that numbers are part of families and numbers have different homes depending on what kind of number they are, just like people do.

Examples of natural numbers

I'll start by talking about myself a little bit. A lot of the time when I meet someone new, they ask me where I live. You don't give them your specific address. I don't tell them 202 Calvert Drive; that doesn't really mean much. But I do tell them that I live in Cupertino. That's probably the most specific name I use to describe where I live.

On the numbers side of things, the most basic number is the number 1, and the most specific descriptor of where it lives is called the natural numbers. The natural numbers are all the numbers that you learn when you're a baby, like 1, 2, 3, 4, 5, 6 and on and on. The natural numbers are also sometimes call the counting numbers because they're the first numbers you learn how to count.

Whole Numbers

Back to me real fast, although I do live in Cupertino, Cupertino is part of Santa Clara County. This means that since I'm a resident of Cupertino, I'm also a resident of Santa Clara County. But the reverse isn't necessarily true, because not everyone that lives in Santa Clara County lives in Cupertino, so you have to be careful going back and forth.

All of the natural numbers are part of the whole numbers.

Numbers are the exact same way. If we get a tiny bit less specific, what we come to are called the whole numbers. All of the natural numbers are part of the whole numbers, just like all the people who live in Cupertino also live in Santa Clara County. But there is one whole number that is not a natural number. That is the number 0. So when we're talking about the whole numbers, we're talking about the numbers that start with 0 and starting going up 1, 2, 3 and on and on.

Integers

Taking a step further back in my situation, Cupertino and Santa Clara County are both parts of California. Again, not everyone that lives in California lives in Santa Clara or, even more specifically, Cupertino. But if you live in Cupertino or Santa Clara, you're definitely living in California.

Taking a step out in terms of the numbers brings us to what are called the integers. Again, not all of the integers are whole numbers and natural numbers. But all of the whole numbers and natural numbers are integers. The integers now also add in the negatives: -1, -2, -3 and on and on in the negative direction as well.

Rational Numbers

Taking another step back with me, I think most people are aware that California is a state that is part of the U.S. So I am also a resident of the United States. Again, everyone that is a resident of California is also a resident of the U.S. But not everyone that lives in the U.S. lives in California.

Rational numbers give us fractions.

That trend continues with the numbers. As we take another step back, we come to what are called the rational numbers. The new additions to the club are fractions. This means we could have things like -1/2 or 1/3 or 3/4 or maybe 11/7.

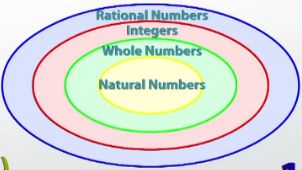The list becomes a little bit harder to write but, again, you could imagine that there are a lot of different kinds of numbers in here. It's still true that all of the previous numbers we mentioned are rationals, but not all of the rationals, specifically these fractions, are part of the numbers in the integers, whole numbers or natural numbers.

Not all of the integers are natural or whole numbers, but all whole and natural numbers are integers.

Irrational Numbers

Now that we've taken where I live all the way out to the fact that I live in America, we probably shouldn't leave out the people that live in different countries. But they're in a different group. For people that live in Japan or France, for example, you're not living in America, so you're part of a separate group.

There's a similar thing going on with the numbers. There's a separate group of numbers that don't fit with the rest of these. Those are called the irrational numbers. Irrational numbers are all the numbers that can't be described as fractions.

There are a lot of different numbers like this. One of the ones you might have heard of is called pi, which is 3.14159... and that's as much as I know, but it does go on forever, and there is no way you can represent pi with a fraction to make it the exact right decimal. Another is the square root of 2, which is something like 1.4, but again, the decimal goes on forever and there's no fraction that can represent it.

These irrational numbers are their own group. They are not part of the rationals, or naturals or whole numbers; they are not related, but separate.

Irrational numbers are separate and cannot be fractions.

Real Numbers

I don't like ending the story on separatism. Regardless of what country you live in, we're all residents of the planet Earth. Numbers are the same way. They're happy and they like to be together. They all live under the banner of what are called the real numbers. The irrational and the rational come together, and with them combined, they form the real numbers.

Lesson Summary

To review, the most specific set of numbers are the natural numbers and they are 1, 2, 3 and so on and so forth. The next step out is the whole numbers, and you simply add 0 to the group; everything else stays the same. When we come to the integers, we add the negatives: -3, -2, -1, 0, 1, 2, 3. Next come the rational numbers, and the rational numbers give us the fractions.

The irrational are separate to this and they are the numbers that can't be fractions, like pi and the square root of 2. The real numbers bring the rational and the irrational together in one big set.