Uncertainty principle
From Wikipedia, the free encyclopedia
| Quantum physics |
 |
| Quantum mechanics |
| Introduction to... |
| Fundamental concepts |
| Decoherence · Interference |
| Experiments |
| Double-slit experiment |
| Equations |
| Schrödinger equation |
| Advanced theories |
| Quantum field theory |
| Interpretations |
| Copenhagen · Ensemble |
| Scientists |
| Planck · Schrödinger |
| |
In quantum physics, the outcome of even an ideal measurement of a system is not deterministic, but instead is characterized by a probability distribution, and the larger the associated standard deviation is, the more "uncertain" we might say that that characteristic is for the system. The Heisenberg uncertainty principle gives a lower bound on the product of the standard deviations of position and momentum for a system, implying that it is impossible to have a particle that has an arbitrarily well-defined position and momentum simultaneously. More precisely, the product of the standard deviations  , where
, where  is the reduced Planck constant. The principle generalizes to many other pairs of quantities besides position and momentum (for example, angular momentum about two different axes), and can be derived directly from the axioms of quantum mechanics.
is the reduced Planck constant. The principle generalizes to many other pairs of quantities besides position and momentum (for example, angular momentum about two different axes), and can be derived directly from the axioms of quantum mechanics.
Note that the uncertainties in question are characteristic of the mathematical quantities themselves. In any real-world measurement, there will be additional uncertainties created by the non-ideal and imperfect measurement process. The uncertainty principle holds true regardless of whether the measurements are ideal (sometimes called von Neumann measurements) or non-ideal (Landau measurements). Note also that the product of the uncertainties, of order 10−35 Joule-seconds, is so small that the uncertainty principle has negligible effect on objects of macroscopic scale, despite its importance for atoms and subatomic particles.
The uncertainty principle was an important step in the development of quantum mechanics when it was discovered by Werner Heisenberg in 1927. It is often confused with the observer effect.
Contents
|
[edit] Wave-particle duality
A fundamental postulate of quantum mechanics, which manifests itself in the Heisenberg Uncertainty Principle, is that no physical phenomenon can be (to arbitrary accuracy) described as a "classic point particle" or as a wave but rather the microphysical situation is best described in terms of wave-particle duality.
The Heisenberg uncertainty principle is a consequence of this picture. The amplitude of the wave associated with a particle corresponds to its position, and the wavelength (more precisely, its Fourier transform) is inversely proportional to momentum. In order to localize the wave so as to have a sharp peak (i.e., a small position uncertainty), it is necessary to incorporate waves with very short wavelengths, corresponding to high momenta in all directions, and therefore a large momentum uncertainty. Indeed, the Heisenberg Uncertainty Principle is equivalent to a theorem in functional analysis that the standard deviation of the squared absolute value of a function, times the standard deviation of the squared absolute value of its Fourier transform, is at least 1/(16π²) (Folland and Sitaram, Theorem 1.1).
A helpful analogy can be drawn between the wave associated with a quantum-mechanical particle and a more familiar wave, the time-varying signal associated with, say, a sound wave. It is meaningless to ask about the frequency spectrum at a single moment in time, because the measure of frequency is the measure of a repetition recurring over a period of time. Indeed, in order for a signal to have a relatively well-defined frequency, it must persist for a long period of time, and conversely, a signal that occurs at a relatively well-defined moment in time (i.e., of short duration) will necessarily encompass a broad frequency band. This is, indeed, a close mathematical analogue of the Heisenberg uncertainty principle. See also Complementarity (physics).
[edit] Uncertainty principle versus observer effect
The uncertainty principle in quantum mechanics is sometimes erroneously explained by claiming that the measurement of position necessarily disturbs a particle's momentum, and vice versa—i.e., that the uncertainty principle is a manifestation of the observer effect. Indeed, Heisenberg himself may have initially offered explanations which suggested this view. Prior to the more modern understanding, a measurement was often visualized as a physical disturbance inflicted directly on the measured system, being sometimes illustrated as a thought experiment called Heisenberg's microscope. For instance, when measuring the position of an electron, one imagines shining a light on it, thus disturbing the electron and producing the quantum mechanical uncertainties in its position.
Equating the uncertainty principle and the observer effect mischaracterizes the way measurement in quantum mechanics is understood. Consider a hypothetical experiment in which a physicist prepares an ensemble of 2N particles in the same way. Suppose further that the physicist is using perfect measuring equipment and that N is sufficiently large so that the net result is statistically significant. For the first N particles of this ensemble, the position would be measured and recorded, giving a probability distribution for position. For the remaining N particles, momentum would be measured, giving a probability distribution for momentum. Finally, the product of the standard deviations would be computed, giving a value of at least  . If the position and momentum had been measured subsequently for the same particle, then the results of the second measurement would not reflect the original state, due to a correct application of the observer effect. But in this experiment, no such claim is made. The physicist never attempts to measure the position and momentum of a single particle but measures them for a different set of N particles from the same initial state. One measurement cannot affect the other. Moreover, although each measurement collapses the quantum state of the particle, the probability distribution resulting from these measurements will correctly reflect the quantum state as it existed before the measurement. Consequently, the uncertainty principle should be considered an intrinsic smearing of statistical information instead of a limitation on measuring equipment.[1]
. If the position and momentum had been measured subsequently for the same particle, then the results of the second measurement would not reflect the original state, due to a correct application of the observer effect. But in this experiment, no such claim is made. The physicist never attempts to measure the position and momentum of a single particle but measures them for a different set of N particles from the same initial state. One measurement cannot affect the other. Moreover, although each measurement collapses the quantum state of the particle, the probability distribution resulting from these measurements will correctly reflect the quantum state as it existed before the measurement. Consequently, the uncertainty principle should be considered an intrinsic smearing of statistical information instead of a limitation on measuring equipment.[1]
The EPR paradox is one indication that it is wrong to view the uncertanty principle as simply a measurement directly disturbing a particle. This "paradox" shows that a measurement can be performed on a particle without disturbing it directly, by performing a measurement on a distant entangled particle.
In any case, it is now understood that the uncertainties in the system exist prior to and independent of the measurement, and the uncertainty principle is therefore independent of the observer effect.
[edit] Generalization, precise formulation, and Robertson-Schrödinger relation
Measurements of position and momentum taken in several identical copies of a system in a given state will each vary according to a probability distribution characteristic of the system’s state. This is the fundamental postulate of quantum mechanics.
If we compute the standard deviations Δx and Δp of the position and momentum measurements, then
where
 (h-bar) is the reduced Planck's constant (Planck's constant divided by 2π).
(h-bar) is the reduced Planck's constant (Planck's constant divided by 2π).
More generally, given any Hermitian operators A and B, and a system in the state ψ, there are probability distributions associated with the measurement of each of A and B, giving rise to standard deviations ΔψA and ΔψB. Then
where the operator [A,B] = AB - BA denotes the commutator of A and B, and  denotes expectation value. This inequality is called the Robertson-Schrödinger relation, and includes the Heisenberg Uncertainty Principle as a special case. It was first pointed out in 1930 by Howard Percy Robertson and (independently) by Erwin Schrödinger.
denotes expectation value. This inequality is called the Robertson-Schrödinger relation, and includes the Heisenberg Uncertainty Principle as a special case. It was first pointed out in 1930 by Howard Percy Robertson and (independently) by Erwin Schrödinger.
[edit] Other uncertainty principles
Due to the Robertson-Schrödinger relation above, an uncertainty relation arises between any two observable quantities that can be defined by non-commuting operators. A few of the more common examples follow:
- There is an uncertainty relation between the position and momentum of an object:
- between angular position and angular momentum of an object:
- between two orthogonal components of the total angular momentum operator of an object:
-
- where i, j, k are distinct and Ji denotes angular momentum along the xi axis.
- between the number of electrons in a superconductor and the phase of its Ginzburg-Landau order parameter[2][3]
[edit] Energy-time uncertainty principle
Unlike the above examples, some uncertainty principles are not direct consequences of the Robertson-Schrödinger relation. The most famous of these is the energy-time uncertainty principle.
Applying the ideas of special relativity to the position-momentum uncertainty principle, many physicists, like Niels Bohr, postulated that the following relation ought to exist:
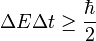 ,
,
but it was not immediately obvious how Δt should be defined (since time is not treated as an operator). In 1926, Dirac offered a precise definition and derivation of this uncertainty relation, as coming from a relativistic quantum theory of "events". But the better-known, more widely-used, correct formulation was given only in 1945 by L. I. Mandelshtam and I. E. Tamm, as follows. For a quantum system in a non-stationary state  and an observable B represented by a self-adjoint operator
and an observable B represented by a self-adjoint operator  , the following formula holds:
, the following formula holds:
 ,
,
where ΔψE is the standard deviation of the energy operator in the state  , ΔψB stands for the standard deviation of the operator
, ΔψB stands for the standard deviation of the operator  and
and  is the expectation value of
is the expectation value of  in that state. Although, the second factor in the left-hand side has dimension of time, it is different from the time parameter that enters Schrödinger equation. It is a lifetime of the state
in that state. Although, the second factor in the left-hand side has dimension of time, it is different from the time parameter that enters Schrödinger equation. It is a lifetime of the state  with respect to the observable B. In other words, this is the time after which the expectation value
with respect to the observable B. In other words, this is the time after which the expectation value  changes appreciably.
changes appreciably.
The energy-time uncertainty principle has important implications for spectroscopy. Since excited states have a finite lifetime, they do not all release exactly the same energy when they decay; rather, the spectroscopic peaks are actually bumps with a finite width (called natural linewidth), with the center of the bump corresponding to the true energy of the excited state. For fast-decaying states, the linewidth makes it difficult to accurately measure this true energy, and indeed, researchers have even used microwave cavities to slow down the decay-rate, in order to get sharper peaks and more accurate energy measurements[4].
One particularly famous false formulation of the energy-time uncertainty principle says that the energy of a quantum system measured over the time interval Δt has to be inaccurate, with the inaccuracy ΔE given by the inequality  . This formulation was explicitly invalidated by Y. Aharonov and D. Bohm in 1961. Indeed, one can actually determine the accurate energy of a quantum system in an arbitrarily short interval of time. Moreover, as recent research indicates, for quantum systems with discrete energy spectra the product ΔEΔt is bounded from above by a statistical noise that in fact vanishes if sufficiently many identical copies of the system are used. This vanishing upper bound certainly removes the possibility of a lower bound, again disproving this false formulation of the energy-time uncertainty principle.
. This formulation was explicitly invalidated by Y. Aharonov and D. Bohm in 1961. Indeed, one can actually determine the accurate energy of a quantum system in an arbitrarily short interval of time. Moreover, as recent research indicates, for quantum systems with discrete energy spectra the product ΔEΔt is bounded from above by a statistical noise that in fact vanishes if sufficiently many identical copies of the system are used. This vanishing upper bound certainly removes the possibility of a lower bound, again disproving this false formulation of the energy-time uncertainty principle.
[edit] Derivation
The uncertainty principle has a straightforward mathematical derivation. The key step is an application of the Cauchy-Schwarz inequality, one of the most useful theorems of linear algebra.
For two arbitrary Hermitian operators A: H → H and B: H → H, and any element x of H, then
In an inner product space the Cauchy-Schwarz inequality holds.
Rearranging this formula leads to:
This gives one form of the Robertson-Schrödinger relation:
where the operator [A,B] = AB - BA denotes the commutator of A and B.
To make the physical meaning of this inequality more directly apparent, it is often written in the equivalent form:
where
is the operator mean of observable X in the system state ψ and
is the operator standard deviation of observable X in the system state ψ. This formulation can be derived from the above formulation by plugging in  for A and
for A and  for B, and using the fact that
for B, and using the fact that
This formulation acquires its physical interpretation, indicated by the suggestive terminology "mean" and "standard deviation", due to the properties of measurement in quantum mechanics. Particular uncertainty relations, such as position-momentum, can usually be derived by a straightforward application of this inequality.
[edit] History and interpretations
The Uncertainty Principle was developed as an answer to the question: How does one measure the location of an electron around a nucleus?
In the summer of 1922 Heisenberg met Niels Bohr, the founding father of quantum mechanics, and in September 1924 Heisenberg went to Copenhagen, where Bohr had invited him as a research associate and later as his assistant. In 1925 Werner Heisenberg laid down the basic principles of a complete quantum mechanics. In his new matrix theory he replaced classical commuting variables with non-commuting ones. Heisenberg's paper marked a radical departure from previous attempts to solve atomic problems by making use of observable quantities only. He wrote in a 1925 letter, "My entire meagre efforts go toward killing off and suitably replacing the concept of the orbital paths that one cannot observe." Rather than struggle with the complexities of three-dimensional orbits, Heisenberg dealt with the mechanics of a one-dimensional vibrating system, an anharmonic oscillator. The result was formulae in which quantum numbers were related to observable radiation frequencies and intensities. In March 1926, working in Bohr's institute, Heisenberg formulated the principle of uncertainty thereby laying the foundation of what became known as the Copenhagen interpretation of quantum mechanics.
Albert Einstein was not happy with the uncertainty principle, and he challenged Niels Bohr and Werner Heisenberg with a famous thought experiment (See the Bohr-Einstein debates for more details): we fill a box with a radioactive material which randomly emits radiation. The box has a shutter, which is opened and soon thereafter shut by a clock at a precise time, thereby allowing some radiation to escape. So the time is already known with precision. We still want to measure the conjugate variable energy precisely. Einstein proposed doing this by weighing the box before and after. The equivalence between mass and energy from special relativity will allow you to determine precisely how much energy was left in the box. Bohr countered as follows: should energy leave, then the now lighter box will rise slightly on the scale. That changes the position of the clock. Thus the clock deviates from our stationary reference frame, and by general relativity, its measurement of time will be different from ours, leading to some unavoidable margin of error. In fact, a detailed analysis shows that the imprecision is correctly given by Heisenberg's relation.
The term Copenhagen interpretation of quantum mechanics was often used interchangeably with and as a synonym for Heisenberg's Uncertainty Principle by detractors who believed in fate and determinism and saw the common features of the Bohr-Heisenberg theories as a threat. Within the widely but not universally accepted Copenhagen interpretation of quantum mechanics (i.e., it was not accepted by Einstein or other physicists such as Alfred Lande), the uncertainty principle is taken to mean that on an elementary level, the physical universe does not exist in a deterministic form — but rather as a collection of probabilities, or potentials. For example, the pattern (probability distribution) produced by millions of photons passing through a diffraction slit can be calculated using quantum mechanics, but the exact path of each photon cannot be predicted by any known method. The Copenhagen interpretation holds that it cannot be predicted by any method, not even with theoretically infinitely precise measurements.
It is this interpretation that Einstein was questioning when he said "I cannot believe that God would choose to play dice with the universe." Bohr, who was one of the authors of the Copenhagen interpretation, responded, "Einstein, don't tell God what to do." Niels Bohr himself acknowledged that quantum mechanics and the uncertainty principle were counter-intuitive when he stated, "Anyone who is not shocked by quantum theory has not understood a single word."
The basic debate between Einstein and Bohr (including Heisenberg's Uncertainty Principle) was that Einstein was in essence saying: "Of course, we can know where something is; we can know the position of a moving particle if we know every possible detail, and therefore by extension, we can predict where it will go." Bohr and Heisenberg were saying: "We can only know the probable position of a moving particle, therefore by extension, we can only know its probable destination; we can never know with absolute certainty where it will go."
Einstein was convinced that this interpretation was in error. His reasoning was that all previously known probability distributions arose from deterministic events. The distribution of a flipped coin or a rolled die can be described with a probability distribution (50% heads, 50% tails), but this does not mean that their physical motions are unpredictable. Ordinary mechanics can be used to calculate exactly how each coin will land, if the forces acting on it are known. And the heads/tails distribution will still line up with the probability distribution (given random initial forces).
Einstein assumed that there are similar hidden variables in quantum mechanics which underlie the observed probabilities and that these variables, if known, would show that there was what Einstein termed "local realism," a description opposite to the uncertainty principle, being that all objects must already have their properties before they are observed or measured. For the greater part of the twentieth century, there were many such hidden variable theories proposed, but in 1964 John Bell theorized the Bell inequality to counter them, which postulated that although the behavior of an individual particle is random, it is also correlated with the behavior of other particles. Therefore, if the uncertainty principle is the result of some deterministic process in which a particle has local realism, it must be the case that particles at great distances instantly transmit information to each other to ensure that the correlations in behavior between particles occur. The interpretation of Bell's theorem explicitly prevents any local hidden variable theory from holding true because it shows the necessity of a system to describe correlations between objects. The implication is, if a hidden local variable is the cause of particle 1 being at a position, then a second hidden local variable would be responsible for particle 2 being in its own position — and there is no system to correlate the behavior between them. Experiments have demonstrated that there is a correlation. In the years following, Bell's theorem was tested and has held up experimentally time and time again, and these experiments are in a sense the clearest experimental confirmation of quantum mechanics. It is worth noting that Bell's theorem only applies to local hidden variable theories; non-local hidden variable theories can still exist (which some, including Bell, think is what can bridge the conceptual gap between quantum mechanics and the observable world).
Whether Einstein's view or Heisenberg's view is true or false is not a directly empirical matter. One criterion by which we may judge the success of a scientific theory is the explanatory power it gives us, and to date it seems that Heisenberg's view has been the better at explaining physical subatomic phenomena.
[edit] Popular culture
The uncertainty principle is stated in popular culture in many ways, for example, by some stating that it is impossible to know both where an electron is and where it is going at the same time. This is roughly correct, although it fails to mention an important part of the Heisenberg principle, which is the quantitative bounds on the uncertainties. Heisenberg stated that it is impossible to determine simultaneously and with unlimited accuracy the position and momentum of a particle, but due to Planck's Constant being so small, the Uncertainty Principle was intended to apply only to the motion of atomic particles. However, culture often misinterprets this to mean that it is impossible to make a completely accurate measurement.
- In the science fiction television series Star Trek: The Next Generation, the fictional transporters used to "beam" characters to different locations overcome the sampling limitations due to the Uncertainty Principle with the use of "Heisenberg compensators." When asked, "How do the Heisenberg compensators work?" by Time magazine on 28 November 1994, Michael Okuda, technical advisor on Star Trek, famously responded, "They work just fine, thank you."[5]
- In the 1997 film The Lost World: Jurassic Park, chaostician Ian Malcolm claims that the effort "to observe and document, not interact" with the dinosaurs is a scientific impossibility because of "the Heisenberg Uncertainty Principle, whatever you study, you also change." This is an inaccurate confusion with the observer effect, as explained above.
- The Michael Frayn play Copenhagen (1998) highlights some of the processes that went into the formation of the Uncertainty Principle. The play dramatizes the meetings between Werner Heisenberg and Niels Bohr. It highlights, as well, the discussion of the work that both did to help build nuclear bombs - Heisenberg for Germany and Bohr for the United States and allied forces.
- In an episode of the television show Aqua Teen Hunger Force, Meatwad (who was temporarily made into a genius) tries to incorrectly explain Heisenberg's Uncertainty Principle to Frylock to explain his new found intelligence. "Heisenberg's Uncertainty Principle tells us that at a specific curvature of space, knowledge can be transferred into energy, or — and this is key now — matter."
- In an episode of Stargate SG-1, Samantha Carter explains, using the Uncertainty Principle, that the future is not predetermined, that one can only calculate possibilities.
- Horror novelist Dennis Etchison makes mention of the Heisenberg principle in a handful of his stories and books.


![\Delta_\psi A \, \Delta_\psi B \geq \frac{1}{2}\left|\left\langle\left[{A},{B}\right]\right\rangle_\psi\right|](http://upload.wikimedia.org/math/f/7/6/f76a67b1d823deafe4e3032186e9f6cb.png)



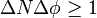



![\frac{1}{4} |\langle [A,B]x | x \rangle|^2\leq \| A x \|^2 \| B x \|^2,](http://upload.wikimedia.org/math/c/4/7/c47ed0dc31bb9d4467ac177c31f460c9.png)
![\Delta_{\psi} A \, \Delta_{\psi} B \ge \frac{1}{2} \left|\left\langle\left[{A},{B}\right]\right\rangle_\psi\right|](http://upload.wikimedia.org/math/1/d/3/1d3f2c1271a50c638f3e2bccd2e72ff4.png)


![[A,B]=[A - \lang A\rang, B - \lang B\rang].](http://upload.wikimedia.org/math/d/7/0/d7020ff856924f5942031209f5281f9a.png)