List of Hund's rules
From Wikipedia, the free encyclopedia
In atomic physics, Hund's rules, (occasionally called the "bus seat rule") refer to a simple set of rules used to determine which is the term symbol that corresponds to the ground state of a multi-electron atom. They are named in honour of Friedrich Hund who contributed Hund's Rule, rule two as listed here.
The four rules are:
- Full shells and subshells do not contribute to total
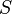 , the total spin angular momentum and
, the total spin angular momentum and 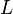 , the total orbital angular momentum quantum numbers.
, the total orbital angular momentum quantum numbers. - The term with maximum multiplicity (maximum
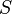 ) has the lowest energy level.
) has the lowest energy level. - For a given multiplicity, the term with the largest value of
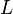 has the lowest energy.
has the lowest energy. - For atoms with less than or equal to half-filled shells, the level with the lowest value of
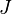 lies lowest in energy. Otherwise, if the outermost shell is more than half-filled the term with highest value of
lies lowest in energy. Otherwise, if the outermost shell is more than half-filled the term with highest value of 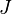 is the one with the lowest energy.
is the one with the lowest energy.
The rules deal in a simple way how the usual energy interactions dictate the ground state term. The rules assume that the repulsion between the outer electrons is very much greater than the spin-orbit interaction which is in turn stronger than any other remaining interactions. This is referred to as the LS coupling regime.
Contents
|
[edit] Rule #1
It can be shown that for full orbitals and suborbitals both the residual electrostatic term (repulsion between electrons) and the spin-orbit interaction can only shift all the energy levels together. Thus when determining the ordering of energy levels in general only the outer valence electrons need to be considered.
[edit] Rule #2
Due to the Pauli exclusion principle, two electrons cannot share the same set of quantum numbers within the same system. Therefore, there is room for only two electrons in each spatial orbital. One of these electrons must have (for some chosen direction z),  , and the other must have
, and the other must have  . Hund's second rule states that the lowest energy atomic state is the one which maximizes the sum of the
. Hund's second rule states that the lowest energy atomic state is the one which maximizes the sum of the 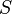 values for all of the electrons in the system, maximizing the number of unpaired electrons. This is usually the lowest energy atomic state because it forces the unpaired electrons to reside in different spatial orbitals. This results in a larger average distance between the two electrons, reducing electron-electron repulsion energy.
values for all of the electrons in the system, maximizing the number of unpaired electrons. This is usually the lowest energy atomic state because it forces the unpaired electrons to reside in different spatial orbitals. This results in a larger average distance between the two electrons, reducing electron-electron repulsion energy.
[edit] Rule #3
This rule deals again with reducing the repulsion between electrons. It can be understood from the classical picture that if all electrons are orbiting in the same direction (higher orbital angular momentum) they meet less often than if some of them orbit in opposite directions. In that last case the repulsive force increases, which separates electrons. This adds potential energy to them, so their energy level is higher
[edit] Rule #4
This rule considers the energy shifts due to spin-orbit coupling. In the case where the spin-orbit coupling is weak compared to the residual electrostatic, where 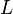 and
and 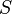 are still good quantum numbers the splitting is given by:
are still good quantum numbers the splitting is given by:
The value of  changes from plus to minus for shells greater than half full. The second term gives the dependence of the ground state on the magnitude of
changes from plus to minus for shells greater than half full. The second term gives the dependence of the ground state on the magnitude of 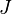 .
.
[edit] Example
As an example, consider the ground state of silicon. The electronic configuration of Si is  . Applying the first rule, only the outer
. Applying the first rule, only the outer 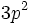 electrons need be considered. The possible multiplets are
electrons need be considered. The possible multiplets are  ; of those,
; of those,  and
and  are not allowed because of the exclusion principle. The second rule now states that the triplet state
are not allowed because of the exclusion principle. The second rule now states that the triplet state 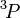 with
with  has the lowest energy. There is no choice of triplets
has the lowest energy. There is no choice of triplets  states, so the third rule is not required. [If the
states, so the third rule is not required. [If the  state were allowed, then the third rule would come into force and state that it was more favourable than the
state were allowed, then the third rule would come into force and state that it was more favourable than the 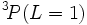 state.] The triplet
state.] The triplet 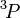 consists of three states,
consists of three states,  . With only two of six possible electrons in the shell, it is less than half-full and thus
. With only two of six possible electrons in the shell, it is less than half-full and thus  is the ground state.
is the ground state.

