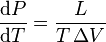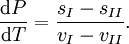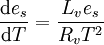Clausius-Clapeyron relation

From Wikipedia, the free encyclopedia

(Redirected from Clausius-Clapeyron equation)

Jump to: navigation, search

In thermodynamics, The Clausius-Clapeyron relation, named after Rudolf Clausius and Émile Clapeyron, is a way of characterizing the phase transition between two states of matter, such as solid and liquid. On a pressure-temperature (P-T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius-Clapeyron relation gives the slope of this curve. Mathematically,

$\frac{\mathrm{d}P}{\mathrm{d}T} = \frac{L}{T\,\Delta V}$

where $d P / d T$ is the slope of the coexistence curve, $L$ is the latent heat, $T$ is the temperature, and $Δ V$ is the volume change of the phase transition.

1 Derivation
2 Applications
- 2.1 Chemistry
- 2.2 Chemical engineering
- 2.3 Meteorology
3 Example
4 References
5 Bibliography

[edit] Derivation

Suppose two phases, I and II, are in contact and at equilibrium with each other. Then the chemical potentials are related by $μ I = μ I I$ . Along the coexistence curve, we also have $dμ I = dμ I I$ . We now use the Gibbs-Duhem relation $dμ = - s d T + v d P$ , where $s$ and $v$ are, respectively, the entropy and volume per particle, to obtain

- (s I - s I I)d T + (v I - v I I)d P = 0.

Hence, rearranging, we have

$\frac{\mathrm{d}P}{\mathrm{d}T} = \frac{s_I-s_{II}}{v_I-v_{II}}.$

From the relation between heat and change of entropy in a reversible process δQ = T dS, we have that the quantity of heat added in the transformation is

L = T (s I - s I I).

Combining the last two equations we obtain the standard relation.

[edit] Applications

[edit] Chemistry

This equation gives the quantitative dependence of the vapor pressure of a liquid on its temperature. It can be used to predict the temperature at a certain pressure, given the temperature at another pressure, or vice versa. If the corresponding temperature and pressure is known at two points, the enthalpy of vaporization can also be determined from this equation.

$\ln \left(\frac{P_2}{P_1} \right) = \left(\frac{\mathcal 4 H_{vap}}{R} \right) \times \left(\frac{1}{T_1} - \frac{1}{T_2} \right)$

where

$T 1$ and $P 1$ are a corresponding temperature (K) and pressure
$T 2$ and $P 2$ are the corresponding temperature and pressure at another point
$\mathcal 4 H_{vap}$ is the enthalpy of vaporization
$R$ is the gas constant (8.314)

[edit] Chemical engineering

A specific derivation of the equation is used in chemistry and chemical engineering to estimate the vapor pressure of a substance based on the heat of vaporization of that substance, and on the temperature of the system under consideration. The equation is as follows:

$\ln p^* = -\frac{\Delta \hat H _v}{RT}+B$

where

$p *$ is the vapor pressure (mmHg)
${\Delta \hat H_v}$ is the enthalpy of vaporization (kJ/mole)
$R$ is the gas constant
$T$ is the temperature (Kelvin)
$B$ is a constant based on the substance and the system parameters

[edit] Meteorology

In meteorology, a specific derivation of the Clausius-Clapeyron equation is used to describe dependence of saturated water vapor pressure on temperature. This is similar to its use in chemistry and chemical engineering.

It plays a crucial role in the current debate on climate change because its solution predicts exponential behavior of saturation water vapor pressure (and, therefore water vapor concentration) as a function of temperature. In turn, because water vapor is a greenhouse gas, it might lead to further increase in the sea surface temperature leading to runaway greenhouse effect. Debate on iris hypothesis and intensity of tropical cyclones dependence on temperature depends in part on “Clausius-Clapeyron” solution.

Clausius-Clapeyron equations is given for typical atmospheric conditions as

$\frac{\mathrm{d}e_s}{\mathrm{d}T} = \frac{L_v e_s}{R_v T^2}$

where:

$e s$ is saturation water vapor pressure
$T$ is a temperature
$L v$ is latent heat of evaporation
$R v$ is water vapor gas constant.

One can solve this equation to give^[1]

$e_s(T)= 6.112 \exp \left( \frac{17.67 T}{T+243.5} \right)$

where:

$e s (T)$ is in hPa
$T$ is in Celsius.

Thus, neglecting the weak variation of (T+243.5) at normal temperatures, one observes that saturation water vapor pressure changes exponentially with $T$ .

[edit] Example

One of the uses of this equation is to determine if a phase transition will occur in a given situation. Consider the question of how much pressure is needed to melt ice at a temperature $Δ T$ below 0°C. We can assume

${\Delta P} = \frac{L}{T\,\Delta V} {\Delta T}$

and substituting in

L

= 3.34×10⁵ J/kg (latent heat of water),

T = 273

K (absolute temperature), and

Δ V

= -9.05×10^-5 m³/kg (change in volume from solid to liquid),

we obtain

$\frac{\Delta P}{\Delta T}$ = -13.1 MPa/°C.

To provide a rough example of how much pressure this is, to melt ice at -7°C (the temperature many ice skating rinks are set at) would require balancing a small car (mass = 1000 kg^[2]) on a thimble (area = 1 cm²).