Exponent Laws Examples

Lesson Objective

This lesson shows you some examples on using the exponent laws that you have learned in the previous lessons.

About This Lesson

After learning the exponent laws in the previous two lessons, it's time to learn on how you can apply them.

This lesson shows you some examples on using these laws.

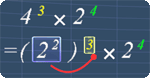
Study Tips

Tip #1

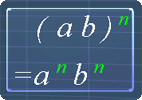
Exponent law shown in the previous lesson

In the last lesson, we have learned three more laws. Let's recall them here. The picture shows one of the law. Here is an example on how to use it:

       a² x (ab)³= a² x a³b³
                       = a^{2 + 3}b³
                       = a⁵b³

Tip #2

As for the next law, here are some examples:

       2⁰ ÷ e⁰ = 1 ÷ 1
                  = 1

       (a¹⁰ q^r+s z^-10 + 5b)⁰ = (whatever)⁰
                                    = 1

Tip #3

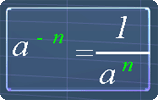
Changing negative exponent to positive exponent

Finally, the picture below shows the last law. Here is an example on how to use it:

Now, watch the following math video see more examples.

Math Video

Lesson Video

If the above player doesn't work, try this direct link.

Math Video Transcript

00:00:01.090
This lesson shows you some example questions on the exponent laws. Now, let's simplify the following.

00:00:09.200
Let's consider this example, 4 to the power of 3 multiply by 2 to the power of 4.

00:00:16.190
Now, if we consider this law, we’ll realize that we can not use it because the base for these terms are not the same.

00:00:24.190
Therefore, we need to find a way to make these bases to be the same. 

00:00:29.170
To do so, notice that 4 here is equals to, 2 multiply by 2, which is also equals to, 2 to the power of 2.

00:00:39.130
Therefore, we can replace 4 with 2 to the power of 2.

00:00:44.130
Alright, notice that to proceed, we need to simplify this term.

00:00:49.150
To do so, we can use this law. 

00:00:53.180
Before we use it, let's match the colors first. 

00:00:58.060
Now, 2 to the power of 2, to the power 3 is equals to, 2 to the power of 2 multiply by 3.

00:01:06.150
2 multiply by 3 gives 6.

00:01:12.040
Now, we can use this exponent law to further simplify these terms. Let's match the colors first.

00:01:20.110
2 to the power of 6 multiply 2 to the power of 4, gives 2 to the power 6 plus 4.

00:01:27.050
Now, 6 plus 4 gives 10. This is the simplest  term. So, the answer is 2 to the power of 10.

00:01:38.200
Next example, let's simplify this.

00:01:42.140
To do so, we can use this exponent law.
00:01:46:040
Now, 3 to the power of 2 to the power of 3 is equals to, 3 to the power of 2 multiply by 3.

00:01:53.240
2 multiply by 3 gives 6.

00:01:58.240
Next, let's simplify this term.

00:02:02.080
3 to the power of negative 3, to the power of 4 is equals to, 3 to the power of negative 3 multiply by  4.
 
00:02:10.150
Now, negative 3 multiply by 4 gives negative 12.

00:02:17.000
To simplify further, we can use this exponent law. 

00:02:21:110
Let's match the colors first.

00:02:25.010
Now, by using the exponent law to simplify these terms, we get 3 to the power of 6 plus negative 12.

00:02:33.070
Notice that, positive multiply by negative gives negative. 

00:02:39.130
With this, when we multiply these terms, we get 3 to the power of 6 minus 12.

00:02:46.060
6 minus 12 gives negative 6. Now we have 3 to the power of negative 6.

00:02:52.220
It is better not to leave the answer in the form of negative exponent. So let’s change this to a positive exponent term. 

00:03:00.160
Now, referring to this exponent law. We can see that, 3 to the power of negative 6  is equals to, 1 divides by 3 to the power of 6. 

00:03:13.240
Alright, next  example. 

00:03:16.100
Let's simplify this term.

00:03:19.200
8 divides by 4 gives 2.  Now, referring to this exponent law, we can see that, p to the power of 5 divides by p to the power of 2 gives p to the power of 5 minus 2.

00:03:32.200
Similarly, q to the power of 8 divides by q to the power of 7 gives q to the power of 8 minus  7. 

00:03:40.010
Let's put this term back.

00:03:42.210
Now, 5 minus 2 gives 3.

00:03:48.210
Similarly, 8 minus 7 gives 1.

00:03:52.230
It is a good practice to  write, q to the power of 1 as "q". So, we can remove the number 1 here.

00:04:00.050
We can no longer simplify this term. So, the answer is 2 p to the power of 3 q. 

00:04:07.020
That’s all for this lesson. Try out the practice questions for reinforce your understanding.

Practice Questions & More

Multiple Choice Questions (MCQ)

Now, let's try some MCQ questions to understand this lesson better.

You can start by going through the series of questions on exponent laws examples or pick your choice of question below.

Question 1 on the basics on exponent laws
Question 2 on the basics on exponent laws

More Lessons