
Determine Equation of Line Practice
Question 1
Given the points (3,-3) and (-3, 1).
Determine the equation of the line that passes through these points.
You can use the picture shown on the right as reference.
Determine the equation of the line that passes through these points.
You can use the picture shown on the right as reference.
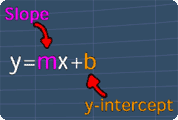
Answer
Select and check your answer...
Check Answer
Step by Step Solution
Step 1
First, to determine the equation of the line, we should start with the Slope-Intercept Form of an equation of a line.
From the picture, we only need to find the values of the slope(m) and y-intercept(b).
After finding them, we just replace m and b with these values. That's it.
From the picture, we only need to find the values of the slope(m) and y-intercept(b).
After finding them, we just replace m and b with these values. That's it.
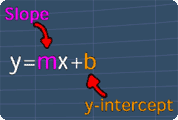
Step 2
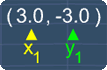
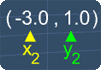
Now, with the given 2 points (3,-3) and (-3,1), we can use them to find m using the Slope Formula as shown on the right.
To use this formula, we need label these points as Point 1 and Point 2. Let's label (3,-3) as Point 1 and (-3,1) as Point 2.
By doing this, we have:
To use this formula, we need label these points as Point 1 and Point 2. Let's label (3,-3) as Point 1 and (-3,1) as Point 2.
By doing this, we have:



Step 3
Now, we substitute these values into the slope formula.
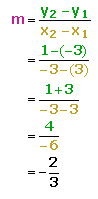
Hence, the we get the slope, m = -2/3
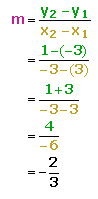
Hence, the we get the slope, m = -2/3
Step 4
With m = -2/3, the equation becomes:

Next, we have to find b. To do so, we can pick a point on the line and substitute its x- and y-coordinates into the equation above.

Next, we have to find b. To do so, we can pick a point on the line and substitute its x- and y-coordinates into the equation above.
Step 5
We can just pick any of the given
points, (3,-3) or (-3, 1). Let's
pick the point (-3, 1) where:
x = -3 and y = 1
Substituting x and y into the equation, we get:
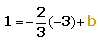
Now, let's solve for b:
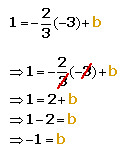
With this, we have the y-intercept, b as -1
x = -3 and y = 1
Substituting x and y into the equation, we get:
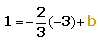
Now, let's solve for b:
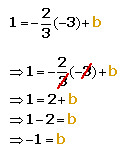
With this, we have the y-intercept, b as -1
Step 6
With b = -1, the equation becomes:
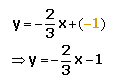
From the equation of the line above, clearly the answer is C.
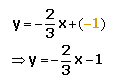
From the equation of the line above, clearly the answer is C.
To close the all the steps, reload
equation of line practice page