In general, there is no single formula for finding the median of a binomial distribution, and it may even be non-unique. However, several special results have been established:
If
Any median
A median
The median is unique and equal to
When
There are also conditional binomials. If
The binomial distribution is a special case of the Poisson binomial distribution, which is a sum of n independent non-identical Bernoulli trials Bern(pi). If X has the Poisson binomial distribution with p1=…=pn=pp1=\ldots =pn=p then ∼B(n,p)\sim B(n, p).
Usually the mode of a binomial B(n, p) distribution is equal to where is the floor function. However, when
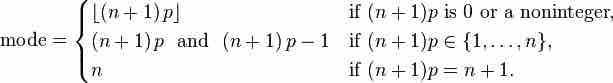
Summary of Modes
This summarizes how to find the mode of a binomial distribution.

Floor Function
Floor function is the lowest previous integer in a series.

Mode
This formula is for calculating the mode of a binomial distribution.
If two binomially distributed random variables X and Y are observed together, estimating their covariance can be useful. Using the definition of covariance, in the case n = 1 (thus being Bernoulli trials) we have .
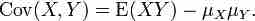
Covariance 1
The first part of finding covariance.
The first term is non-zero only when both X and Y are one, and μX and μY are equal to the two probabilities. Defining pB as the probability of both happening at the same time, this gives and for n independent pairwise trials .
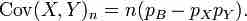
Covariance 3
The final formula for the covariance of a binomial distribution.
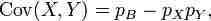
Covariance 2
The next step in determining covariance.
If X and Y are the same variable, this reduces to the variance formula given above.