Cohen's d

Cohen's $d$ is a method of estimating effect size in a $t$-test based on means or distances between/among means . An effect size is a measure of the strength of a phenomenon—for example, the relationship between two variables in a statistical population (or a sample-based estimate of that quantity). An effect size calculated from data is a descriptive statistic that conveys the estimated magnitude of a relationship without making any statement about whether the apparent relationship in the data reflects a true relationship in the population. In that way, effect sizes complement inferential statistics such as $p$-values. Among other uses, effect size measures play an important role in meta-analysis studies that summarize findings from a specific area of research, and in statistical power analyses.

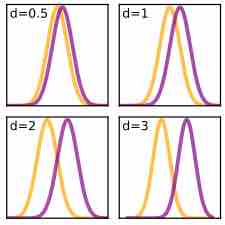
Cohen's $d$

Plots of the densities of Gaussian distributions showing different Cohen's effect sizes.

The concept of effect size already appears in everyday language. For example, a weight loss program may boast that it leads to an average weight loss of 30 pounds. In this case, 30 pounds is an indicator of the claimed effect size. Another example is that a tutoring program may claim that it raises school performance by one letter grade. This grade increase is the claimed effect size of the program. These are both examples of "absolute effect sizes," meaning that they convey the average difference between two groups without any discussion of the variability within the groups.

Reporting effect sizes is considered good practice when presenting empirical research findings in many fields. The reporting of effect sizes facilitates the interpretation of the substantive, as opposed to the statistical, significance of a research result. Effect sizes are particularly prominent in social and medical research.

Cohen's $d$ is an example of a standardized measure of effect. Standardized effect size measures are typically used when the metrics of variables being studied do not have intrinsic meaning (e.g., a score on a personality test on an arbitrary scale), when results from multiple studies are being combined, when some or all of the studies use different scales, or when it is desired to convey the size of an effect relative to the variability in the population. In meta-analysis, standardized effect sizes are used as a common measure that can be calculated for different studies and then combined into an overall summary.

As in any statistical setting, effect sizes are estimated with error, and may be biased unless the effect size estimator that is used is appropriate for the manner in which the data were sampled and the manner in which the measurements were made. An example of this is publication bias, which occurs when scientists only report results when the estimated effect sizes are large or are statistically significant. As a result, if many researchers are carrying out studies under low statistical power, the reported results are biased to be stronger than true effects, if any.

Relationship to Test Statistics

Sample-based effect sizes are distinguished from test statistics used in hypothesis testing in that they estimate the strength of an apparent relationship, rather than assigning a significance level reflecting whether the relationship could be due to chance. The effect size does not determine the significance level, or vice-versa. Given a sufficiently large sample size, a statistical comparison will always show a significant difference unless the population effect size is exactly zero. For example, a sample Pearson correlation coefficient of $0.1$ is strongly statistically significant if the sample size is $1000$. Reporting only the significant $p$-value from this analysis could be misleading if a correlation of $0.1$ is too small to be of interest in a particular application.

Cohen's D

Cohen's $d$ is defined as the difference between two means divided by a standard deviation for the data:

$D=\dfrac { { \bar { x } }_{ 1 }-{ \bar { x } }_{ 2 } }{ \sigma }$

Cohen's $d$ is frequently used in estimating sample sizes. A lower Cohen's $d$ indicates a necessity of larger sample sizes, and vice versa, as can subsequently be determined together with the additional parameters of desired significance level and statistical power.

The precise definition of the standard deviation s was not originally made explicit by Jacob Cohen; he defined it (using the symbol $\sigma$) as "the standard deviation of either population" (since they are assumed equal). Other authors make the computation of the standard deviation more explicit with the following definition for a pooled standard deviation with two independent samples.

$\displaystyle{s=\sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 -1) s_2^2}{n_1 + n_2 - 2}}}$