In statistics, statistical inference is the process of drawing conclusions from data that is subject to random variation--for example, observational errors or sampling variation. More substantially, the terms statistical inference, statistical induction, and inferential statistics are used to describe systems of procedures that can be used to draw conclusions from data sets arising from systems affected by random variation, such as observational errors, random sampling, or random experimentation. Initial requirements of such a system of procedures for inference and induction are that the system should produce reasonable answers when applied to well-defined situations and that it should be general enough to be applied across a range of situations.
The outcome of statistical inference may be an answer to the question "what should be done next? " where this might be a decision about making further experiments or surveys, or about drawing a conclusion before implementing some organizational or governmental policy.
Suppose you have been hired by the National Election Commission to examine how the American people feel about the fairness of the voting procedures in the U.S. How will you do it? Who will you ask?
It is not practical to ask every single American how he or she feels about the fairness of the voting procedures. Instead, we query a relatively small number of Americans, and draw inferences about the entire country from their responses. The Americans actually queried constitute our sample of the larger population of all Americans. The mathematical procedures whereby we convert information about the sample into intelligent guesses about the population fall under the rubric of inferential statistics.
In the case of voting attitudes, we would sample a few thousand Americans, drawn from the hundreds of millions that make up the country. In choosing a sample, it is therefore crucial that it be representative. It must not over-represent one kind of citizen at the expense of others. For example, something would be wrong with our sample if it happened to be made up entirely of Florida residents. If the sample held only Floridians, it could not be used to infer the attitudes of other Americans. The same problem would arise if the sample were comprised only of Republicans. Inferential statistics are based on the assumption that sampling is random. We trust a random sample to represent different segments of society in close to the appropriate proportions (provided the sample is large enough).
Furthermore, when generalizing a trend found in a sample to the larger population, statisticians uses tests of significance (such as the Chi-Square test or the T-test). These tests determine the probability that the results found were by chance, and therefore not representative of the entire population.
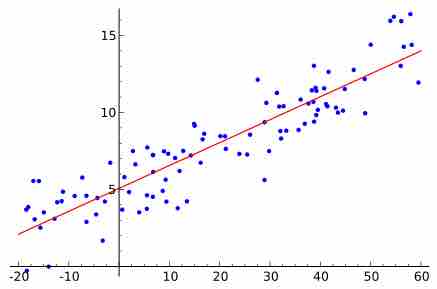
Linear Regression in Inferential Statistics
This graph shows a linear regression model, which is a tool used to make inferences in statistics.