Statistics deals with all aspects of the collection, organization, analysis, interpretation, and presentation of data. It includes the planning of data collection in terms of the design of surveys and experiments.
Statistics can be used to improve data quality by developing specific experimental designs and survey samples. Statistics also provides tools for prediction and forecasting. Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences as well as government and business. Statistical consultants can help organizations and companies that don't have in-house expertise relevant to their particular questions.
Descriptive and Inferential Statistics
Statistical methods can summarize or describe a collection of data. This is called descriptive statistics . This is particularly useful in communicating the results of experiments and research. Statistical models can also be used to draw statistical inferences about the process or population under study—a practice called inferential statistics. Inference is a vital element of scientific advancement, since it provides a way to draw conclusions from data that are subject to random variation. Conclusions are tested in order to prove the propositions being investigated further, as part of the scientific method. Descriptive statistics and analysis of the new data tend to provide more information as to the truth of the proposition.
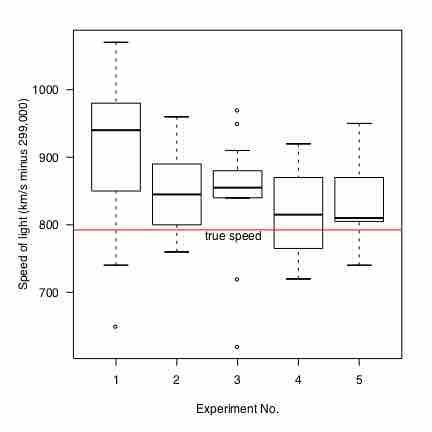
Summary statistics
In descriptive statistics, summary statistics are used to summarize a set of observations, in order to communicate the largest amount as simply as possible. This Boxplot represents Michelson and Morley's data on the speed of light. It consists of five experiments, each made of 20 consecutive runs.
The Statistical Process
When applying statistics to a scientific, industrial, or societal problems, it is necessary to begin with a population or process to be studied. Populations can be diverse topics such as "all persons living in a country" or "every atom composing a crystal". A population can also be composed of observations of a process at various times, with the data from each observation serving as a different member of the overall group. Data collected about this kind of "population" constitutes what is called a time series. For practical reasons, a chosen subset of the population called a sample is studied—as opposed to compiling data about the entire group (an operation called census). Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. This data can then be subjected to statistical analysis, serving two related purposes: description and inference.
Descriptive statistics summarize the population data by describing what was observed in the sample numerically or graphically. Numerical descriptors include mean and standard deviation for continuous data types (like heights or weights), while frequency and percentage are more useful in terms of describing categorical data (like race). Inferential statistics uses patterns in the sample data to draw inferences about the population represented, accounting for randomness. These inferences may take the form of: answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation) and modeling relationships within the data (for example, using regression analysis). Inference can extend to forecasting, prediction and estimation of unobserved values either in or associated with the population being studied. It can include extrapolation and interpolation of time series or spatial data and can also include data mining.
Statistical Analysis
Statistical analysis of a data set often reveals that two variables of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation could be caused by a third, previously unconsidered phenomenon, called a confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables.
To use a sample as a guide to an entire population, it is important that it truly represent the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any random trending within the sample and data collection procedures. There are also methods of experimental design for experiments that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population. Randomness is studied using the mathematical discipline of probability theory. Probability is used in "mathematical statistics" (alternatively, "statistical theory") to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method.