As discussed, a histogram is a bar graph displaying tabulated frequencies. Histograms tend to form shapes, which when measured can describe the distribution of data within a dataset. The shape of the distribution can assist with identifying other descriptive statistics, such as which measure of central tendency is appropriate to use.

The distribution of data item values may be symmetrical or asymmetrical. Two common examples of symmetry and asymmetry are the "normal distribution" and the "skewed distribution. "

Central Tendency and Normal Distributions

In a symmetrical distribution the two sides of the distribution are a mirror image of each other. A normal distribution is a true symmetric distribution of data item values. When a histogram is constructed on values that are normally distributed, the shape of columns form a symmetrical bell shape. This is why this distribution is also known as a "normal curve" or "bell curve. " is an example of a normal distribution:

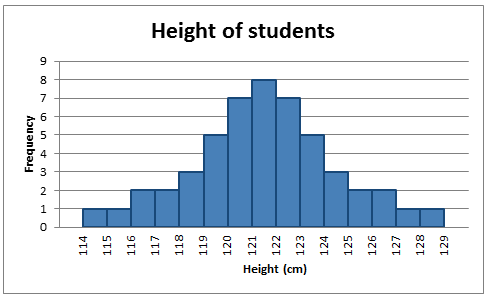
The Normal Distribution

A histogram showing a normal distribution, or bell curve.

If represented as a 'normal curve' (or bell curve) the graph would take the following shape (where $\mu$ is the mean and $\sigma$ is the standard deviation):

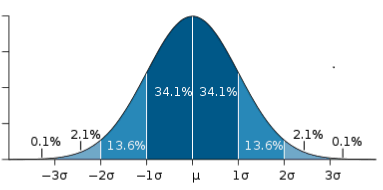
The Bell Curve

The shape of a normally distributed histogram.

A key feature of the normal distribution is that the mode, median and mean are the same and are together in the center of the curve.

Also, there can only be one mode (i.e. there is only one value which is most frequently observed). Moreover, most of the data are clustered around the center, while the more extreme values on either side of the center become less rare as the distance from the center increases (i.e. about 68% of values lie within one standard deviation ($\sigma$) away from the mean; about 95% of the values lie within two standard deviations; and about 99.7% are within three standard deviations. This is known as the empirical rule or the 3-sigma rule).

Central Tendency and Skewed Distributions

In an asymmetrical distribution the two sides will not be mirror images of each other. Skewness is the tendency for the values to be more frequent around the high or low ends of the $x$-axis. When a histogram is constructed for skewed data it is possible to identify skewness by looking at the shape of the distribution. For example, a distribution is said to be positively skewed when the tail on the right side of the histogram is longer than the left side. Most of the values tend to cluster toward the left side of the $x$-axis (i.e, the smaller values) with increasingly fewer values at the right side of the $x$-axis (i.e. the larger values).

A distribution is said to be negatively skewed when the tail on the left side of the histogram is longer than the right side. Most of the values tend to cluster toward the right side of the $x$-axis (i.e. the larger values), with increasingly less values on the left side of the $x$-axis (i.e. the smaller values).

A key feature of the skewed distribution is that the mean and median have different values and do not all lie at the center of the curve.

There can also be more than one mode in a skewed distribution. Distributions with two or more modes are known as bi-modal or multimodal, respectively. The distribution shape of the data in is bi-modal because there are two modes (two values that occur more frequently than any other) for the data item (variable).

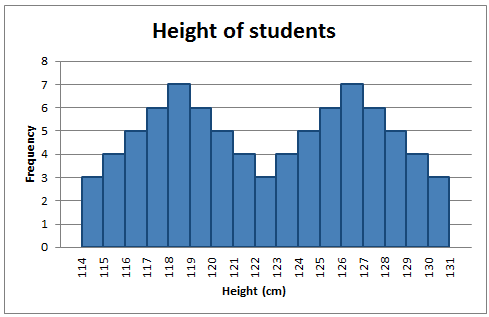
Bi-modal Distribution

Some skewed distributions have two or more modes.