The Regression Method
The best way to understand the regression method is to use an example. Let's say we have some data about students' Math SAT scores and their freshman year GPAs in college. The average SAT score is 560, with a standard deviation of 75. The average first year GPA is 2.8, with a standard deviation of 0.5. Now, we choose a student at random and wish to predict his first year GPA. With no other information given, it is best to predict using the average. We predict his GPA is 2.8
Now, let's say we pick another student. However, this time we know her Math SAT score was 680, which is significantly higher than the average. Instead of just predicting 2.8, this time we look at the graph of averages and predict her GPA is whatever the average is of all the students in our sample who also scored a 680 on the SAT. This is likely to be higher than 2.8.
To generalize the regression method:
- If you know no information (you don't know the SAT score), it is best to make predictions using the average.
- If you know the independent variable, or
$x$ -value (you know the SAT score), the best prediction of the dependent variable, or$y$ -value (in this case, the GPA), is the average of all the$y$ -values for that specific$x$ -value.
Generalization
In the example above, the college only has experience with students that have been admitted; however, it could also use the regression model for students that have not been admitted. There are some problems with this type of generalization. If the students admitted all had SAT scores within the range of 480 to 780, the regression model may not be a very good estimate for a student who only scored a 350 on the SAT.
Despite this issue, generalization is used quite often in statistics. Sometimes statisticians will use interpolation to predict data points within the range of known data points. For example, if no one before had received an exact SAT score of 650, we would predict his GPA by looking at the GPAs of those who scored 640 and 660 on the SAT.
Extrapolation is also frequently used, in which data points beyond the known range of values is predicted. Let's say the highest SAT score of a student the college admitted was 780. What if we have a student with an SAT score of 800, and we want to predict her GPA? We can do this by extending the regression line. This may or may not be accurate, depending on the subject matter.
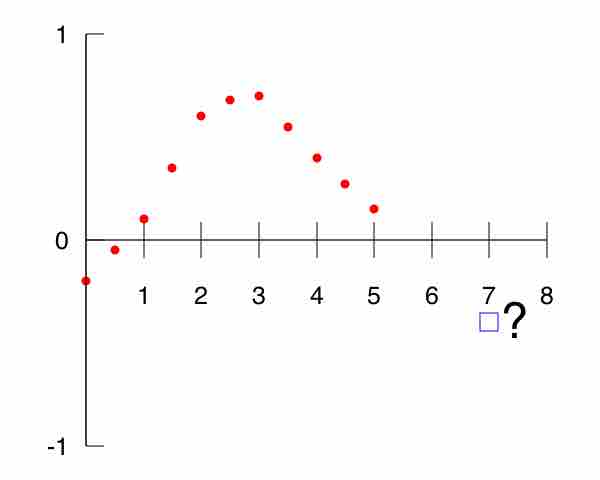
Extrapolation
An example of extrapolation, where data outside the known range of values is predicted. The red points are assumed known and the extrapolation problem consists of giving a meaningful value to the blue box at