The following is an example on how to compute a normal approximation for a binomial distribution.
Assume you have a fair coin and wish to know the probability that you would get 8 heads out of 10 flips. The binomial distribution has a mean of
Standard deviations above the mean of the distribution. The question then is, "What is the probability of getting a value exactly 1.8973 standard deviations above the mean?" You may be surprised to learn that the answer is 0 (the probability of any one specific point is 0). The problem is that the binomial distribution is a discrete probablility distribution whereas the normal distribultion is a continuous distribution.
The solution is to round off and consider any value from 7.5 to 8.5 to represent an outcome of 8 heads. Using this approach, we calculate the area under a normal curve from 7.5 to 8.5. The area in green in the figure is an approximation of the probability of obtaining 8 heads.
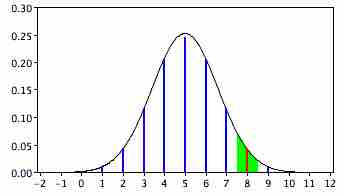
Normal Approximation
Approximation for the probability of 8 heads with the normal distribution.
To calculate this area, first we compute the area below 8.5 and then subtract the area below 7.5. This can be done by finding
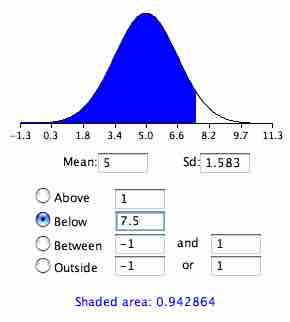
Normal Area 2
This graph shows the area below 7.5.

Normal Area 1
This graph shows the area below 8.5.
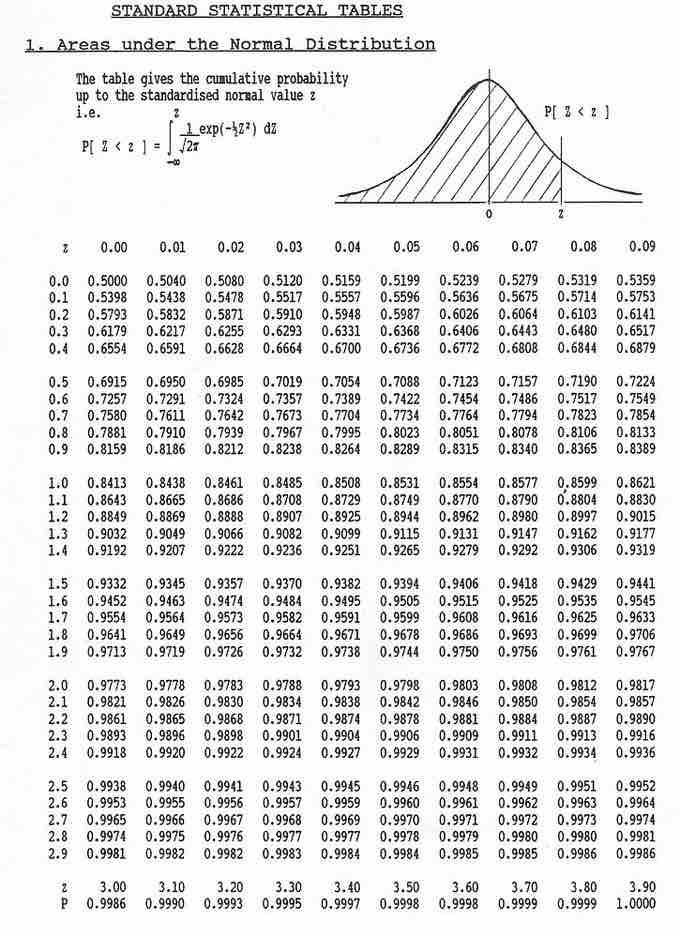
$z$ -Score Table
The
The differences between the areas is 0.044, which is the approximation of the binomial probability. For these parameters, the approximation is very accurate. If we did not have the normal area calculator, we could find the solution using a table of the standard normal distribution (a
- Find a
$Z$ score for 7.5 using the formula$Z=\frac { 7.5-5 }{ 1.5811 } =1.5811$ - Find the area below a
$Z$ of$1.58=0.943$ . - Find a
$Z$ score for 8.5 using the formula$Z=\frac { 8.5-5 }{ 1.5811 } =2.21$ - Find the area below a
$Z$ of$2.21=0.987$ . - Subtract the value in step 2 from the value in step 4 to get 0.044.
The same logic applies when calculating the probability of a range of outcomes. For example, to calculate the probability of 8 to 10 flips, calculate the area from 7.5 to 10.5.