In statistical hypothesis testing, tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance; this can help to decide whether results contain enough information to cast doubt on conventional wisdom, given that conventional wisdom has been used to establish the null hypothesis. The critical region of a hypothesis test is the set of all outcomes which cause the null hypothesis to be rejected in favor of the alternative hypothesis.
Accepting the Null Hypothesis vs. Failing to Reject It
It is important to note the philosophical difference between accepting the null hypothesis and simply failing to reject it. The "fail to reject" terminology highlights the fact that the null hypothesis is assumed to be true from the start of the test; if there is a lack of evidence against it, it simply continues to be assumed true. The phrase "accept the null hypothesis" may suggest it has been proved simply because it has not been disproved, a logical fallacy known as the argument from ignorance. Unless a test with particularly high power is used, the idea of "accepting" the null hypothesis may be dangerous. Nonetheless, the terminology is prevalent throughout statistics, where its meaning is well understood.
Alternatively, if the testing procedure forces us to reject the null hypothesis (
What Does This Mean?
If the
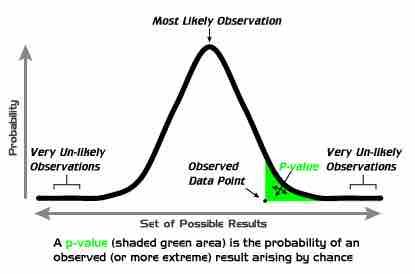
$p$ -Values
A graphical depiction of the meaning of
If the
Whether rejection of the null hypothesis truly justifies acceptance of the research hypothesis depends on the structure of the hypotheses. Rejecting the hypothesis that a large paw print originated from a bear does not immediately prove the existence of Bigfoot. The two hypotheses in this case are not exhaustive; there are other possibilities. Maybe a moose made the footprints. Hypothesis testing emphasizes the rejection which is based on a probability rather than the acceptance which requires extra steps of logic.