Physics Textbooks Boundless Physics Work and Energy Potential Energy and Conservation of Energy
Physics Textbooks Boundless Physics Work and Energy
Physics Textbooks Boundless Physics
Physics Textbooks
Physics
Concept Version 9
Created by Boundless

Springs

When a spring is stretched/compressed from its equilibrium position by x, its potential energy is give as $U = \frac{1}{2} kx^2$.

Learning Objective

  • Explain how potential energy is stored in springs

Key Points

    • The displacement of spring x is usually measured from the position of "neutral length" or "relaxed length". Often, it is most convenient to identify this position as the origin of coordinate reference (x=0).
    • If the block is gently released from the stretched position (x = xf), energy conservation tells us that $\frac{1}{2} m v^2 + \frac{1}{2}k x^2 \\ = \frac{1}{2} k x_f^2 = constant.$.
    • If the block is released from the stretched position (x=xf), by the time the block reaches x=0 position, its speed will be $v(x=0) =\sqrt{\frac{k}{m}}x_f$. The block will keep oscillating between x = -xf and xf.

Terms

  • conservative force

    A force with the property that the work done in moving a particle between two points is independent of the path taken.

  • Hooke's law

    the principle that the stress applied to a solid is directly proportional to the strain produced. This law describes the behavior of springs and solids stressed within their elastic limit.

Full Text

Spring force is conservative force, given by the Hooke's law : F = -kx, where k is spring constant, measured experimentally for a particular spring and x is the displacement . We would like to obtain an expression for the work done to the spring. From the conservation of mechanical energy (Check our Atom on "Conservation of Mechanical Energy), the work should be equal to the potential energy stored in spring. The displacement x is usually measured from the position of "neutral length" or "relaxed length" - the length of spring corresponding to situation when spring is neither stretched nor compressed. We shall identify this position as the origin of coordinate reference (x=0).

Hooke's Law

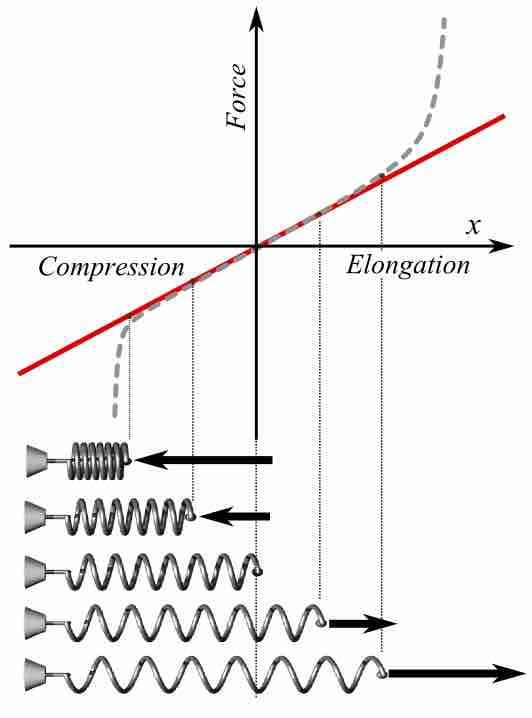
Plot of applied force F vs. elongation X for a helical spring according to Hooke's law (solid line) and what the actual plot might look like (dashed line). Red is used extension, blue for compression. At bottom, schematic pictures of spring states corresponding to some points of the plot; the middle one is in the relaxed state (no force applied).

Let x = 0 and x = xf (>0) be the initial and final positions of the block attached to the string. As the block slowly moves, we do work W on the spring: $W = \int_{0}^{x_f} (kx) dx = \frac{1}{2} k x_f^2$. When we stretch the spring. We have to apply force in the same direction as the displacement. (Technically, work is given as the inner product of the two vectors: force and displacement.$W = \bf{F}\cdot \Delta \bf{x}$). Therefore, the overall sign in the integral is +, not -.

If the block is gently released from the stretched position (x = xf), the stored potential energy in the spring will start to be converted to the kinetic energy of the block, and vice versa. Neglecting frictional forces, Mechanical energy conservation demands that, at any point during its motion,$\begin{aligned} Total ~Energy &= \frac{1}{2} m v^2 + \frac{1}{2}k x^2 \\ &= \frac{1}{2} k x_f^2 = constant. \end{aligned}$

From the energy conservation, we can estimate that, by the time the block reaches x=0 position, its speed will be $v(x=0) =\sqrt{\frac{k}{m}}x_f$. The block will keep oscillating between x = -xf and xf.

[ edit ]
Edit this content
Prev Concept
Gravity
Conservation of Mechanical Energy
Next Concept