A potential energy curve plots the potential energy of an object as a function of that object's position. For example, see . The system under consideration is a closed system, so the total energy of the system remains constant. This means that the kinetic and potential energy always have to sum to be the same value. We observe that the potential energy increases as the kinetic energy decreases and vice versa. The utility of a potential energy curve is that we can quickly determine the potential energy of the object in question at a given position.
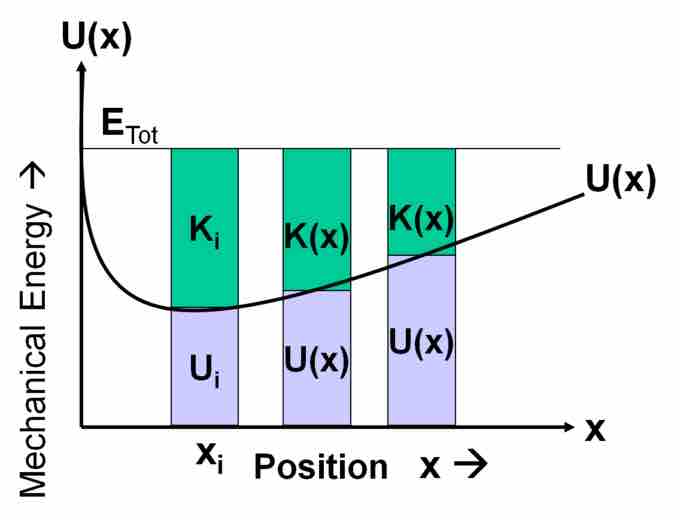
Potential Energy Curve
This figure illustrates the potential energy of a particle as a function of position. The kinetic energy is also shown and is abbreviated K.
Equipotential lines trace lines of equal potential energy. In , if you were to draw a straight horizontal line through the center, that would be an equipotential line. In and , if you travel along an equipotential line, the electric potential will be constant.
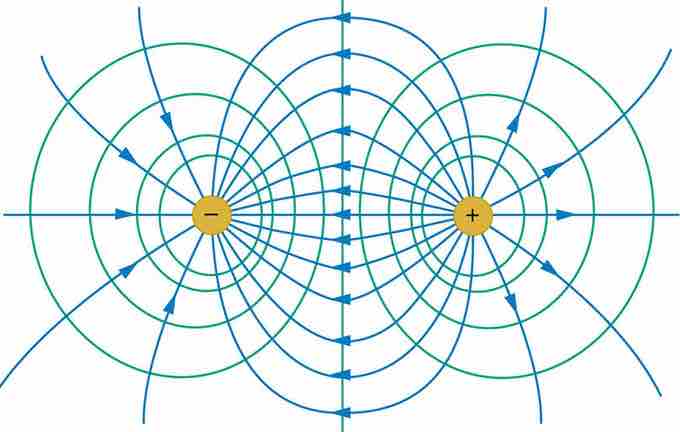
Equipotential Lines for Two Equal and Opposite Point Charges
Electric field (blue) and equipotential lines (green) for two equal and opposite charges
Let us examine the physical explanation for the equipotentials lines in . The equation for the potential of a point charge is V = kQ/r, where V is the potential, k is a constant with a value of 8.99 · 109 N m2/C2, Q is the magnitude of the point charge, and r is the distance from the charge. So, every point that is the same distance from the point charge will have the same electric potential energy. Therefore, if we draw a circle around the point charge, every point on the circle will have the same potential energy.
Work (W) is a measure of the change in potential energy (ΔPE): W = -ΔPE. Since the potential energy does not change along an equipotential line, you do not need to do any work to move along one. However, you do need to do work to move from one equipotential line to another. Recall that work is zero if force is perpendicular to motion; in the figures shown above, the forces resulting from the electric field are in the same direction as the electric field itself. So we note that each of the equipotential lines must be perpendicular to the electric field at every point.