Rotational Angle and Angular Velocity
When an object rotates about an axis, as with a tire on a car or a record on a turntable, the motion can be described in two ways. A point on the edge of the rotating object will have some velocity and will be carried through an arc by riding the spinning object. The point will travel through a distance of
Angle θ and Arc Length s
The radius of a circle is rotated through an angle
The speed at which the object rotates is given by the angular velocity, which is the rate of change of the rotational angle with respect to time. Although the angle itself is not a vector quantity, the angular velocity is a vector. The direction of the angular velocity vector is perpendicular to the plane of rotation, in a direction which is usually specified by the right-hand rule. Angular acceleration gives the rate of change of angular velocity. The angle, angular velocity, and angular acceleration are very useful in describing the rotational motion of an object.
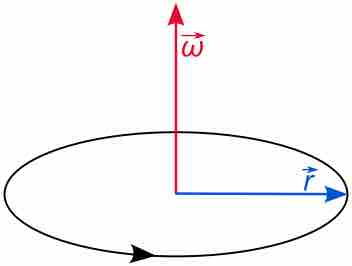
The Direction of Angular Velocity
The angular velocity describes the speed of rotation and the orientation of the instantaneous axis about which the rotation occurs. The direction of the angular velocity will be along the axis of rotation. In this case (counter-clockwise rotation), the vector points upwards.
When the axis of rotation is perpendicular to the position vector, the angular velocity may be calculated by taking the linear velocity
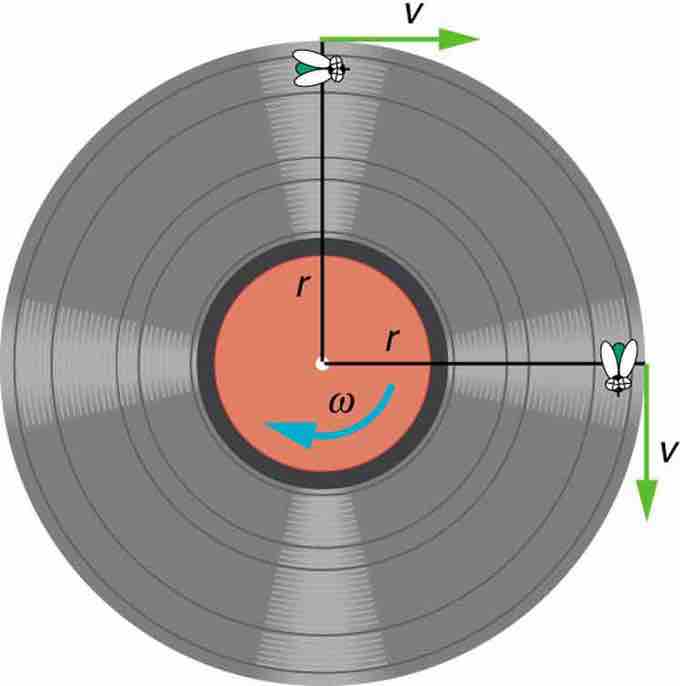
Angular Velocity
A fly on the edge of a rotating object records a constant velocity