Orbital Maneuvers

An orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft (the rest of the flight is called "coasting").

Learning Objective

Explain purpose of an orbital maneuver

Key Points

The ideal rocket equation related the maximum change in velocity attainable by a rocket (delta-v or Δv) as a function of the exhaust velocity (v_e) and the ratio between the mass of the rocket with and without the propellant (m₀/m₁). The equation is given by $\Delta v=v_{e}ln(\frac{m_{0}}{m_{1}})$.
The Oberth effect: where the use of a rocket engine travelling at high speed generates more useful energy than one at low speed. Thus it is more efficient to apply thrust when the spacecraft is nearest to the planet (periastron).
A gravity assist maneuver is the use of the relative movement and gravity of a planet (or other celestial body) to alter the velocity of a spacecraft—typically in order to save propellant, time, and expense. This technique was employed by the Voyager probes (see.
The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes, in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses which move aspacecraft onto and off the transfer orbit. See.

Terms

Hohmann transfer orbit
The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes, in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses, one to move a spacecraft onto the transfer orbit and a second to move off it.
delta-v
The maximum change in the scalar speed of a rocket if the rocket were operated in a vacuum away from external forces (i.e., if no other external forces act).

Full Text

Orbital Maneuvers

In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft. The rest of the flight, especially in a transfer orbit, is called coasting.

Rocket Equation

The Tsiolkovsky rocket equation or ideal rocket equation is an equation useful for considering vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself (a thrust) by expelling part of its mass with high speed and moving due to the conservation of momentum. Specifically, it is a mathematical equation relating the delta-v with the effective exhaust velocity and both the initial and final mass of a rocket (or other reaction engine).

For any such maneuver (or journey involving a number of such maneuvers):

$\Delta v=v_{e}ln(\frac{m_{0}}{m_{1}})$,

where:

m₀ is the initial total mass, including propellant;
m₁ is the final total mass;
v_e is the effective exhaust velocity (v_e=I_{sp •} g₀ where I_sp is the specific impulse expressed as a time period and g0 is the gravitational constant); and
Δv is delta-v the maximum change of speed of the vehicle (with no external forces acting).

See for an illustration plotting the relationship between final velocity and rocket mass ratios (according to the rocket equation).

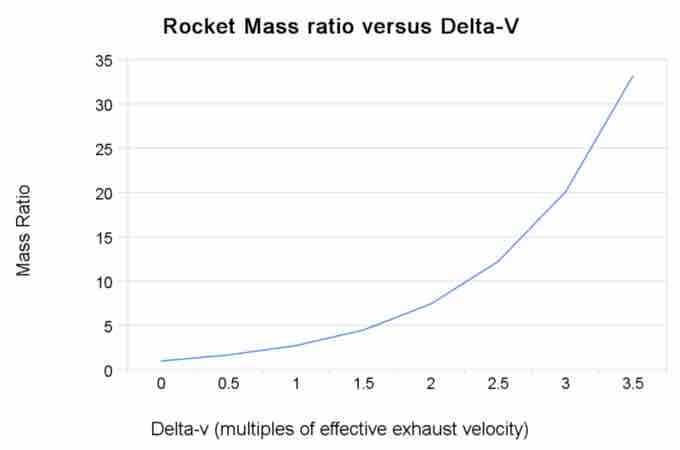
Rocket Equation

Rocket mass ratios versus final velocity calculated from the rocket equation

Delta-v Budget:

The total delta-v for each maneuver estimated for a mission is called a delta-v budget. With a good approximation of the delta-v budget, designers can estimate the fuel to payload requirements of the spacecraft using the rocket equation.

Oberth Effect and Gravitational Assist

In astronautics, the Oberth effect occurs when the use of a rocket engine travelling at high speed generates much more useful energy than one at low speed. This effect is the result of propellant having more usable energy (due to its kinetic energy on top of its chemical potential energy). The vehicle is able to employ this kinetic energy to generate more mechanical power.

Oberth effect is used in a powered flyby or Oberth maneuver in which the application of an impulse (typically from the use of a rocket engine) close to a gravitational body (where the gravity potential is low and the speed is high) allows for more change in kinetic energy and final speed (i.e. higher specific energy) than the same impulse applied further from the body for the same initial orbit.

In orbital mechanics, a gravitational slingshot (or gravity assist maneuver) is the use of the relative movement and gravity of a planet or other celestial body to alter the path and speed of a spacecraft, typically in an effort to save propellant, time, and expense. Gravity assistance can be used to accelerate, decelerate and/or re-direct the path of a spacecraft. This technique was used by the Voyager probes in their fly-bys of Jupiter and Saturn (see ).

Voyager Path Using Gravity Assists

The trajectories that enabled NASA's twin Voyager spacecraft to tour the four gas giant planets and achieve velocity to escape our solar system

Transfer Orbits

Orbit insertion is a general term used for a maneuver when it is more than a small correction. It may be used in a maneuver to change a transfer orbit or an ascent orbit into a stable one, but also to change a stable orbit into a descent (i.e., descent orbit insertion). Also, the term orbit injection is used, especially for changing a stable orbit into a transfer orbit—e.g., trans-lunar injection (TLI), trans-Mars injection (TMI) and trans-Earth injection (TEI).

The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses that move aspacecraft onto and off the transfer orbit, as diagramed in . Hohmann transfer orbits are the most efficient with fuel. Other non-Hohmann types of transfer orbits that are less efficient with fuel exist, but these may be more efficient with other resources (such as time).

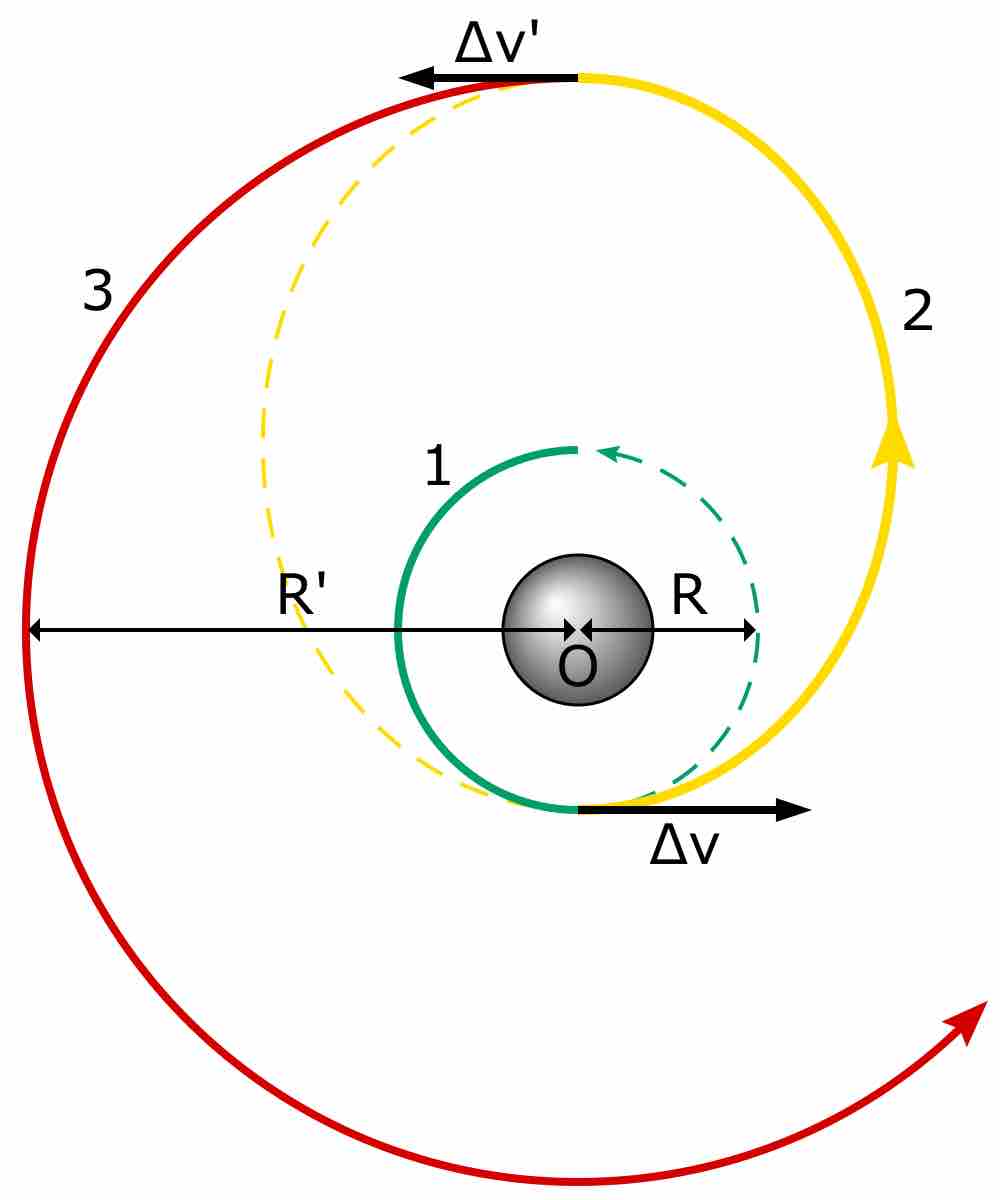
Hohmann Transfer Orbit

A diagram of the Hohmann Transfer Orbit.

Orbital inclination change is an orbital maneuver aimed at changing an orbiting body's orbit inclination (this maneuver is also known as an orbital plane change as the plane of the orbit is tipped). The maneuver requires a change in the orbital velocity vector (delta-v) at the orbital nodes (i.e., the point at which the initial and desired orbits intersect: the line of orbital nodes is defined by the intersection of the two orbital planes).

[ edit ]

Prev Concept

Kepler's Third Law

Satellites

Next Concept