Angular Quantities
Under uniform circular motion, angular and linear quantities have simple relations. When objects rotate about some axis, each point in the object follows a circular arc. The rotation angle is the amount of rotation and is analogous to linear distance. We define the rotation angle
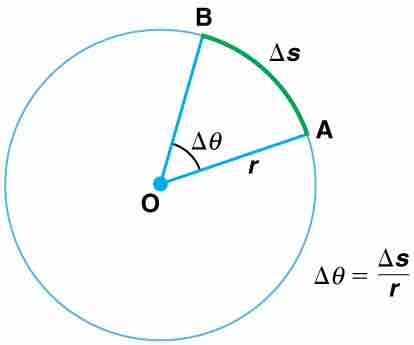
Angle $\theta$ and Arc Length $s$
The radius of a circle is rotated through an angle
We define angular velocity
Under uniform circular motion, the angular velocity is constant. The acceleration can be written as:
This acceleration, responsible for the uniform circular motion, is called centripetal acceleration.
Centripetal Force
Any force or combination of forces can cause a centripetal or radial acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth's gravity on the Moon, friction between roller skates and a rink floor, a banked roadway's force on a car, and forces on the tube of a spinning centrifuge.
Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of curvature, the same as the direction of centripetal acceleration. According to Newton's second law of motion, net force is mass times acceleration. For uniform circular motion, the acceleration is the centripetal acceleration: