Escape Speed

Escape speed is the required starting speed required by an object to go from a starting point in a gravitational potential field to an ending point that is infinitely far away. It is assumed that the velocity of the object at the ending point will be zero.

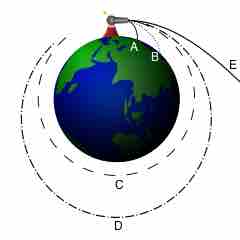
Isaac Newton's Analysis of Escape Speed

In this figure, Objects A and B don't have the required escape speed and so they fall back to Earth after launch. Objects C and D don't either, they achieve a circular and an elliptical orbit respectively. Object E is launched with sufficient escape velocity and escapes the Earth.

Imagine a situation in which a spaceship that does not have a propulsion system is launched straight away from a planet. (It is moot to discuss escape speed for objects with propulsion systems.) Let us assume that the only significant force that is acting on the spaceship is the force of gravity from the planet. The escape speed of the spaceship can calculated through a simple analysis of conservation of energy. The gravitational potential energy of the spaceship is:

$\displaystyle U = \frac{-GMm}{r}$

Where $G$ is the universal gravitational constant ($G = 6.67 \cdot 10^{-11} \text{m}^3\text{kg}^{-1}\text{s}^{-2}$), $M$ is the mass of the planet, $m$ is the mass of the spaceship, and $r$ is the distance of the spaceship from the planet's center of gravity.

At the ending point of the spaceship, $r$ goes to infinity. As $r$ goes to infinity, the value of the gravitational potential energy expression goes to 0.

The kinetic energy of the spaceship can be found from:

$\displaystyle \frac{1}{2}mv^2$

Where $m$ is the mass of the spaceship and $v$ is the velocity of the spaceship.

At the starting point of the spaceship, the velocity must have a magnitude equal to the escape speed ($s_e$). The velocity of the spaceship is 0 at its ending point, and so consequently its kinetic energy is 0 in the end as well.

Summarizing the kinetic energy ($K$) and potential energy ($U$) of the spaceship at it's initial ($i$) and final ($f$) states:

$\displaystyle (K + U)_i = \frac{1}{2}ms_e^2 + \frac{-GMm}{r}$

$(K + U)_f= 0 + 0$

Due to conservation of energy, the initial energy must equal the final energy and so we can solve for $s_e$:

$\displaystyle s_e = \sqrt{\frac{2GM}{r}}$

Interestingly, if the spaceship were to fall to the planet from a point infinitely far away it would obtain a final speed of ses_e at the planet.

It should be noted that if an object is launched from a rotating body, such as the Earth, the speed at which the body rotates will affect the required velocity that an object must have relative to the surface of the body. If a rocket is launched tangentially from the Earth's equator in the same direction that the Earth is turning, it will require a lower velocity relative to the Earth than if it were launched in the opposite direction to meet escape speed requirements.

Additionally, it is a misconception that powered vehicles (such as rockets) require escape speed to leave orbit and travel through outer-space. If the vehicle has a propulsion system to provide it with energy once it has left the surface of the planet, it is not necessary to initially meet escape speed requirements.