In addition to adding vectors, vectors can also be multiplied by constants known as scalars. Scalars are distinct from vectors in that they are represented by a magnitude but no direction. Examples of scalars include an object's mass, height, or volume.
When multiplying a vector by a scalar, the direction of the vector is unchanged and the magnitude is multiplied by the magnitude of the scalar . This results in a new vector arrow pointing in the same direction as the old one but with a longer or shorter length. You can also accomplish scalar multiplication through the use of a vector's components. Once you have the vector's components, multiply each of the components by the scalar to get the new components and thus the new vector.
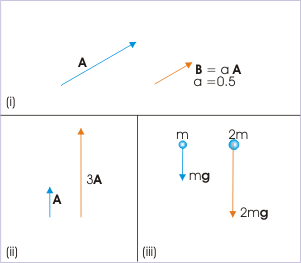
Scalar Multiplication
(i) Multiplying the vector A by 0.5 halves its length. (ii) Multiplying the vector A by 3 triples its length. (iii) Increasing the mass (scalar) increases the force (vector).
A useful concept in the study of vectors and geometry is the concept of a unit vector. A unit vector is a vector with a length or magnitude of one. The unit vectors are different for different coordinates. In Cartesian coordinates the directions are x and y usually denoted