We have previously discussed projectile motion and its key components and basic equations. Using that information, we can solve many problems involving projectile motion. Before we do this, let's review some of the key factors that will go into this problem-solving.

What is Projectile Motion?

Projectile motion is when an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning, after which the only influence on the trajectory is that of gravity.

What are the Key Components of Projectile Motion?

The key components that we need to remember in order to solve projectile motion problems are:

• Initial launch angle, $\theta$
• Initial velocity, $u$
• Time of flight, $T$
• Acceleration, $a$
• Horizontal velocity, $v_x$
• Vertical velocity, $v_y$
• Displacement, $d$
• Maximum height, $H$
• Range, $R$

Now, let's look at two examples of problems involving projectile motion.

Example 1

Let's say you are given an object that needs to clear two posts of equal height separated by a specific distance. Refer to for this example. The projectile is thrown at $25\sqrt{2}$ m/s at an angle of 45°. If the object is to clear both posts, each with a height of 30m, find the minimum: (a) position of the launch on the ground in relation to the posts and (b) the separation between the posts. For simplicity's sake, use a gravity constant of 10. Problems of any type in physics are much easier to solve if you list the things that you know (the "givens").

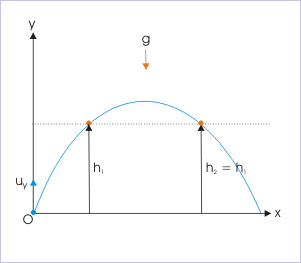
Diagram for Example 1

Use this figure as a reference to solve example 1. The problem is to make sure the object is able to clear both posts.

Solution: The first thing we need to do is figure out at what time $t$ the object reaches the specified height. Since the motion is in a parabolic shape, this will occur twice: once when traveling upward, and again when the object is traveling downward. For this we can use the equation of displacement in the vertical direction, $y-y_0$_:

$y-y_0=(v_y\cdot t)-(\frac{1}{2}\cdot g\cdot {t^2})$

We substitute in the appropriate variables:

$v_y=u\cdot \sin\theta = 25\sqrt{2} \text{ m/s} \cdot \sin\ 45^{\circ}=25 \text{ m/s}$

Therefore:

$30 \text{m} = 25\cdot t-\frac{1}{2}\cdot 10\cdot {t^2}$

We can use the quadratic equation to find that the roots of this equation are 2s and 3s. This means that the projectile will reach 30m after 2s, on its way up, and after 3s, on its way down.

Example 2

An object is launched from the base of an incline, which is at an angle of 30°. If the launch angle is 60° from the horizontal and the launch speed is 10 m/s, what is the total flight time? The following information is given: $u=10 \frac{\text{m}}{\text{s}}$; $\theta = 60$°; $g = 10 \frac{\text{m}}{\text{s}^2}$.

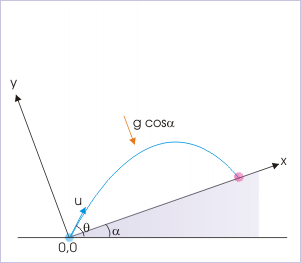
Diagram for Example 2

When dealing with an object in projectile motion on an incline, we first need to use the given information to reorient the coordinate system in order to have the object launch and fall on the same surface.

Solution: In order to account for the incline angle, we have to reorient the coordinate system so that the points of projection and return are on the same level. The angle of projection with respect to the $x$ direction is $\theta - \alpha$, and the acceleration in the $y$ direction is $g\cdot \cos{\alpha}$. We replace $\theta$ with $\theta - \alpha$ and $g$ with $g \cdot \cos{\alpha}$:

$\displaystyle{{T=\frac{2\cdot u\cdot \sin(\theta)}{g}=\frac{2\cdot u\cdot \sin(\theta-\alpha)}{g\cdot \cos(\alpha)}\\ T=\frac{2\cdot 10\cdot \sin(60-30)}{10\cdot \cos(30)}}=\frac{20\cdot \sin(30)}{10\cdot \cos(30)}\\ T=\frac2{\sqrt3}\text{s}}$