Thermal expansion is the tendency of matter to change in volume in response to a change in temperature. (An example of this is the buckling of railroad track, as seen in . ) Atoms and molecules in a solid, for instance, constantly oscillate around its equilibrium point. This kind of excitation is called thermal motion. When a substance is heated, its constituent particles begin moving more, thus maintaining a greater average separation with their neighboring particles. The degree of expansion divided by the change in temperature is called the material's coefficient of thermal expansion; it generally varies with temperature.

Fig 1
Thermal expansion of long continuous sections of rail tracks is the driving force for rail buckling. This phenomenon resulted in 190 train derailments during 1998–2002 in the US alone.
Expansion, Not Contraction
Why does matter usually expand when heated? The answer can be found in the shape of the typical particle-particle potential in matter. Particles in solids and liquids constantly feel the presence of other neighboring particles. This interaction can be represented mathematically as a potential curve. Fig 2 illustrates how this inter-particle potential usually takes an asymmetric form rather than a symmetric form, as a function of particle-particle distance. Note that the potential curve is steeper for shorter distance. In the diagram, (b) shows that as the substance is heated, the equilibrium (or average) particle-particle distance increases. Materials which contract or maintain their shape with increasing temperature are rare. This effect is limited in size, and only occurs within limited temperature ranges.
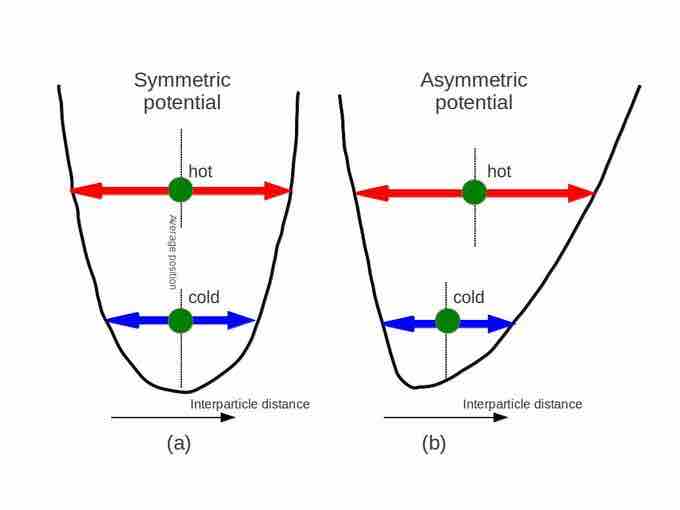
Fig 2
Typical inter-particle potential in condensed matter (such as solid or liquid).
Linear Expansion
To a first approximation, the change in length measurements of an object (linear dimension as opposed to, for example, volumetric dimension) due to thermal expansion is related to temperature change by a linear expansion coefficient. It is the fractional change in length per degree of temperature change. Assuming negligible effect of pressure, we may write:
where L is a particular length measurement and dL/dT is the rate of change of that linear dimension per unit change in temperature. From the definition of the expansion coefficient, the change in the linear dimension
This equation works well as long as the linear-expansion coefficient does not change much over the change in temperature. If it does, the equation must be integrated.