Relativistic Momentum

Relativistic Momentum

Newtonian physics assumes that absolute time and space exist outside of any observer. This gives rise to Galilean relativity, which states that the laws of motion are the same in all inertial frames. It also results in a prediction that the speed of light can vary from one reference frame to another. However, this is contrary to observation. In the theory of special relativity, Albert Einstein keeps the postulate that the equations of motion do not depend on the reference frame, but assumes that the speed of light c is invariant. As a result, position and time in two reference frames are related by the Lorentz transformation instead of the Galilean transformation.

Albert Einstein

Albert Einstein in 1921

Consider, for example, a reference frame moving relative to another at velocity v in the x direction. The Galilean transformation gives the coordinates of the moving frame as

$t' = t$

$x' = x -vt$

while the Lorentz transformation gives

$t' = \gamma (t - \frac{vx}{c^{2}})$

$x' = \gamma (x - vt)$

where $\gamma$ is the Lorentz factor:

$\gamma = \frac{1}{\sqrt{1 - (v/c)^{2}}}$.

Conservation laws in physics, such as the law of conservation of momentum, must be invariant. That is, the property that needs to be conserved should remain unchanged regardless of changes in the conditions of measurement. This means that the conservation law needs to hold in any frame of reference. Newton's second law [with mass fixed in the expression for momentum (p=m*v)], is not invariant under a Lorentz transformation. However, it can be made invariant by making the inertial mass m of an object a function of velocity:

$m = \gamma m_{0}$

where $m_{0}$ is the object's invariant mass.

The modified momentum,

$p = \gamma m_{0}v$

obeys Newton's second law:

$F = \frac{dp}{dt}$.

It is important to note that for speeds much less than the speed of light, Newtonian momentum and relativistic momentum are approximately the same. As one approaches the speed of light, however, relativistic momentum becomes infinite while Newtonian momentum continues to increases linearly. Thus, it is necessary to employ the expression for relativistic momentum when one is dealing with speeds near the speed of light .

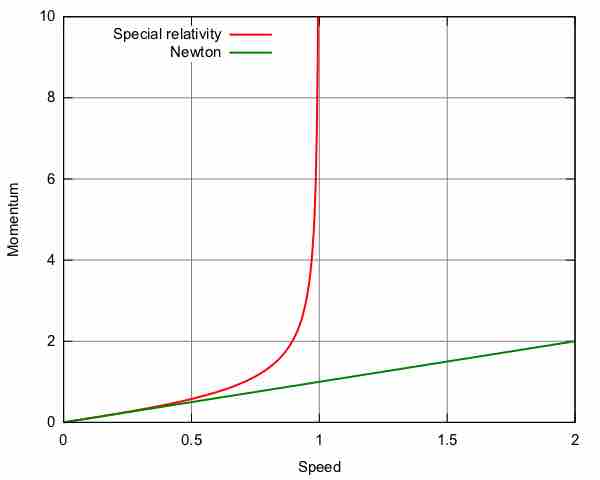
Relativistic and Newtonian Momentum

This figure illustrates that relativistic momentum approaches infinity as the speed of light is approached. Newtonian momentum increases linearly with speed.