Moment of Inertia

The Moment of Inertia

The moment of inertia is a property of the distribution of mass in space that measures mass's resistance to rotational acceleration about one or more axes. Newton's first law, which describes the inertia of a body in linear motion, can be extended to the inertia of a body rotating about an axis using the moment of inertia. That is, an object that is rotating at constant angular velocity will remain rotating unless it is acted upon by an external torque. In this way, the moment of inertia plays the same role in rotational dynamics as mass does in linear dynamics: it describes the relationship between angular momentum and angular velocity as well as torque and angular acceleration .

The moment of inertia I of an object can be defined as the sum of mr² for all the point masses of which it is composed, where m is the mass and r is the distance of the mass from the center of mass. It can be expressed mathematically as: I = ∑mr². Here, I is analogous to m in translational motion.

As an example, consider a hoop of radius r. Assuming that the hoop material is uniform, the hoop's moment of inertia can be found by summing up all the mass of the hoop and multiplying by the distance of that mass from the center of mass. Since the hoop is a circle and the mass is uniform around the circle, the moment of inertia is mr^2. All of the mass m is at a distance r from the center.

Moment of inertia also depends on the axis about which you rotate an object. Objects will usually rotate about their center of mass, but can be made to rotate about any axis. The moment of inertia in the case of rotation about a different axis other than the center of mass is given by the parallel axis theorem. The theorem states that the moment of inertia for an object rotated about a different axis parallel to the axis passing through the center of mass is $I_{cm}+mr^2$where r is now the distance between the two axes and $I_{cm}$is the moment of inertia when rotated about the center of mass which you learned how to calculate in the previous paragraph.

A general relationship among the torque, moment of inertia, and angular acceleration is: net τ = Iα, or α = (net τ)/ I. Net τ is the total torque from all forces relative to a chosen axis. Such torques are either positive or negative and add like ordinary numbers. The relationship in τ = Iα is the rotational analog to Newton's second law and is very applicable. This equation is actually valid for any torque, applied to any object, and relative to any axis.

As can be expected, the larger the torque, the larger the angular acceleration. For example, the harder a child pushes on a merry-go-round, the slower it accelerates for the same torque. The basic relationship between the moment of inertia and the angular acceleration is that the larger the moment of inertia, the smaller the angular acceleration. The moment of inertia depends not only on the mass of an object, but also on its distribution of mass relative to the axis around which it rotates. For example, it wil be much easier to accelerate a merry-go-round full of children if they stand close to its axis than if they all stand at the outer edge .

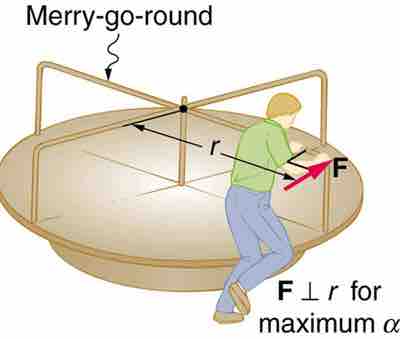
Moment of Inertia on a Merry-Go-Round

A father pushes a playground merry-go-round at its edge and perpendicular to its radius to achieve maximum torque.