Magnetic Field Lines
Einstein is said to have been fascinated by a compass as a child, perhaps musing on how the needle felt a force without direct physical contact. His ability to think deeply and clearly about action at a distance, particularly for gravitational, electric, and magnetic forces, later enabled him to create his revolutionary theory of relativity. Since magnetic forces act at a distance, we define a magnetic field to represent magnetic forces. A pictorial representation of magnetic field lines is very useful in visualizing the strength and direction of the magnetic field . The direction of magnetic field lines is defined to be the direction in which the north end of a compass needle points. The magnetic field is traditionally called the B-field.
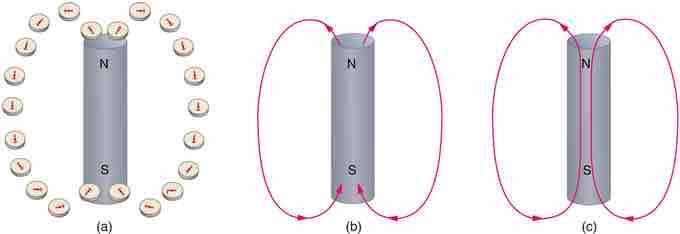
Visualizing Magnetic Field Lines
Magnetic field lines are defined to have the direction that a small compass points when placed at a location. (A) If small compasses are used to map the magnetic field around a bar magnet, they will point in the directions shown: away from the north pole of the magnet, toward the south pole of the magnet (recall that Earth's north magnetic pole is really a south pole in terms of definitions of poles on a bar magnet. ) (B) Connecting the arrows gives continuous magnetic field lines. The strength of the field is proportional to the closeness (or density) of the lines. (C) If the interior of the magnet could be probed, the field lines would be found to form continuous closed loops.
Mapping the magnetic field of an object is simple in principle. First, measure the strength and direction of the magnetic field at a large number of locations (or at every point in space). Then, mark each location with an arrow (called a vector) pointing in the direction of the local magnetic field with its magnitude proportional to the strength of the magnetic field (producing a vector field). You can "connect" the arrows to form magnetic field lines. The direction of the magnetic field at any point is parallel to the direction of nearby field lines, and the local density of field lines can be made proportional to its strength.
Magnetic field lines are like the contour lines (constant altitude) on a topographic map in that they represent something continuous, and a different mapping scale would show more or fewer lines. An advantage of using magnetic field lines as a representation is that many laws of magnetism (and electromagnetism) can be stated completely and concisely using simple concepts such as the "number" of field lines through a surface. These concepts can be quickly translated to their mathematical form. For example, the number of field lines through a given surface is the surface integral of the magnetic field .

Bar Magnet and Magnetic Field Lines
The direction of magnetic field lines represented by the alignment of iron filings sprinkled on paper placed above a bar magnet.
Various phenomena have the effect of "displaying" magnetic field lines as though the field lines are physical phenomena. For example, iron filings placed in a magnetic field line up to form lines that correspond to "field lines. " Magnetic fields' lines are also visually displayed in polar auroras, in which plasma particle dipole interactions create visible streaks of light that line up with the local direction of Earth's magnetic field.
Small compasses used to test a magnetic field will not disturb it. (This is analogous to the way we tested electric fields with a small test charge. In both cases, the fields represent only the object creating them and not the probe testing them. ) Figure 15051 shows how the magnetic field appears for a current loop and a long straight wire, as could be explored with small compasses. A small compass placed in these fields will align itself parallel to the field line at its location, with its north pole pointing in the direction of B. Note the symbols used for field into and out of the paper. We'll explore the consequences of these various sources of magnetic fields in further sections .
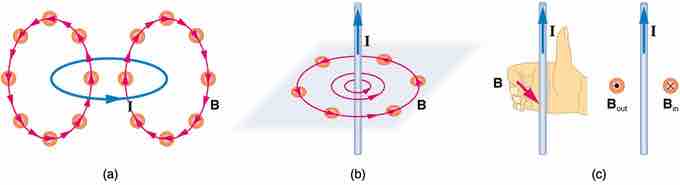
Mapping Magnetic Field Lines
Small compasses could be used to map the fields shown here. (A) The magnetic field of a circular current loop is similar to that of a bar magnet. (B) A long and straight wire creates a field with magnetic field lines forming circular loops. (C) When the wire is in the plane of the paper, the field is perpendicular to the paper. Note that the symbols used for the field pointing inward (like the tail of an arrow) and the field pointing outward (like the tip of an arrow).
Extensive exploration of magnetic fields has revealed a number of hard-and-fast rules. We use magnetic field lines to represent the field (the lines are a pictorial tool, not a physical entity in and of themselves). The properties of magnetic field lines can be summarized by these rules:
- The direction of the magnetic field is tangent to the field line at any point in space. A small compass will point in the direction of the field line.
- The strength of the field is proportional to the closeness of the lines. It is exactly proportional to the number of lines per unit area perpendicular to the lines (called the areal density).
- Magnetic field lines can never cross, meaning that the field is unique at any point in space.
- Magnetic field lines are continuous, forming closed loops without beginning or end. They go from the north pole to the south pole.
The last property is related to the fact that the north and south poles cannot be separated. It is a distinct difference from electric field lines, which begin and end on the positive and negative charges. If magnetic monopoles existed, then magnetic field lines would begin and end on them.