Direction of the Magnetic Force: The Right Hand Rule
So far we have described the magnitude of the magnetic force on a moving electric charge, but not the direction. The magnetic field is a vector field, thus the force applied will be oriented in a particular direction. There is a clever way to determine this direction using nothing more than your right hand . The direction of the magnetic force F is perpendicular to the plane formed by v and B, as determined by the right hand rule, which is illustrated in the figure above. The right hand rule states that: to determine the direction of the magnetic force on a positive moving charge, ƒ, point the thumb of the right hand in the direction of v, the fingers in the direction of B, and a perpendicular to the palm points in the direction of F.
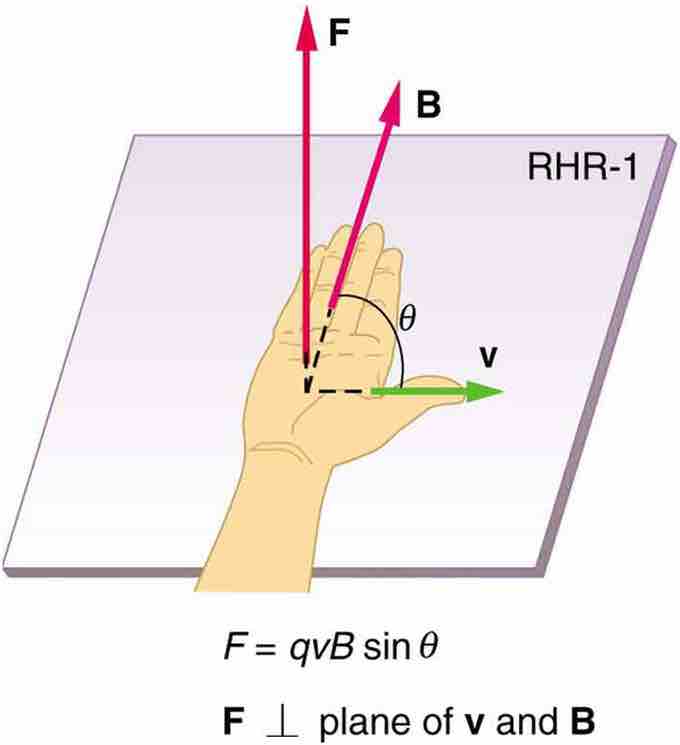
Right Hand Rule
Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is proportional to q, v, B, and the sine of the angle between v and B.
One way to remember this is that there is one velocity, represented accordingly by the thumb. There are many field lines, represented accordingly by the fingers. The force is in the direction you would push with your palm. The force on a negative charge is in exactly the opposite direction to that on a positive charge. Because the force is always perpendicular to the velocity vector, a pure magnetic field will not accelerate a charged particle in a single direction, however will produce circular or helical motion (a concept explored in more detail in future sections). It is important to note that magnetic field will not exert a force on a static electric charge. These two observations are in keeping with the rule that magnetic fields do no work.