In the previous atom on "Center of Mass and Translational Motion," we learned why the concept of center of mass (COM) helps solving mechanics problems involving a rigid body. Here, we will study the rigorous definition of COM and how to determine the location of it.
Definition
The center of mass is a statement of spatial arrangement of mass (i.e. distribution of mass within the system). The position of COM is given a mathematical formulation which involves distribution of mass in space:
where rCOM and ri are vectors representing the position of COM and i-th particle respectively, and M and mi are the total mass and mass of the i-th particle, respectively. This mean means that position of COM is mass weighted average of the positions of particles.
Object with Continuous Mass Distribution
If the mass distribution is continuous with the density ρ(r) within a volume V, the position of COM is given as
where M is the total mass in the volume. If a continuous mass distribution has uniform density, which means ρ is constant, then the center of mass is the same as the center of the volume.
Locating the Center of Mass
The experimental determination of the center of mass of a body uses gravity forces on the body and relies on the fact that in the parallel gravity field near the surface of Earth the center of mass is the same as the center of gravity.
The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.
In two dimensions: An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass .
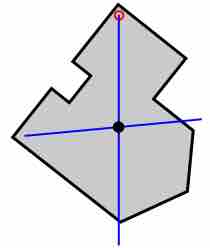
Plumb Line Method for Center of Mass
Suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass.
In three dimensions: By supporting an object at three points and measuring the forces that resist the weight of the object, COM of the three-dimensional coordinates of the center of mass can be determined.