The Heisenberg Uncertainty Principle

The uncertainty principle is any of a variety of mathematical inequalities, asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position x and momentum p or energy E and time t, can be known simultaneously. The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. This can be formulated as the following inequality: $\sigma_x \sigma_y \geq \frac{\hbar}{2}$, where σ_x is the standard deviation of position, σ_p is the standard deviation of momentum, and $\hbar = \frac{h}{2\pi}$. The uncertainty principle is inherent in the properties of all wave-like systems, and it arises in quantum mechanics simply due to the matter wave nature of all quantum objects. Thus, the uncertainty principle actually states a fundamental property of quantum systems, and is not a statement about the observational success of current technology.

The principle is quite counterintuitive, so the early students of quantum theory had to be reassured that naive measurements to violate it were bound always to be unworkable. One way in which Heisenberg originally illustrated the intrinsic impossibility of violating the uncertainty principle is by using an imaginary microscope (see ) as a measuring device.

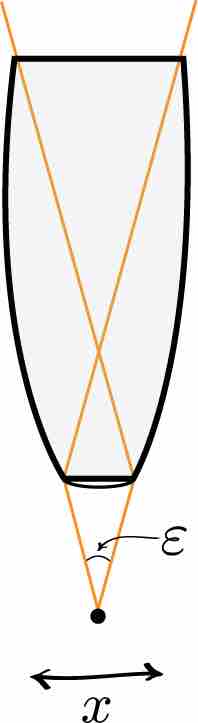
Heisenberg Microscope

Heisenberg's microscope, with cone of light rays focusing on a particle with angle \epsilon

He imagines an experimenter trying to measure the position and momentum of an electron by shooting a photon at it.

Example One

If the photon has a short wavelength and therefore a large momentum, the position can be measured accurately. But the photon scatters in a random direction, transferring a large and uncertain amount of momentum to the electron. If the photon has a long wavelength and low momentum, the collision does not disturb the electron's momentum very much, but the scattering will reveal its position only vaguely.

Example Two

If a large aperture is used for the microscope, the electron's location can be well resolved (see Rayleigh criterion); but by the principle of conservation of momentum, the transverse momentum of the incoming photon and hence the new momentum of the electron resolves poorly. If a small aperture is used, the accuracy of both resolutions is the other way around.

Heisenberg's Argument

Heisenberg's argument is summarized as follows. He begins by supposing that an electron is like a classical particle, moving in the x direction along a line below the microscope, as in the illustration to the right. Let the cone of light rays leaving the microscope lens and focusing on the electron makes an angle $\epsilon$ with the electron. Let $\lambda$ be the wavelength of the light rays. Then, according to the laws of classical optics, the microscope can only resolve the position of the electron up to an accuracy of $\delta x = \frac{\lambda}{sin (\epsilon/2)}$ When an observer perceives an image of the particle, it's because the light rays strike the particle and bounce back through the microscope to their eye. However, we know from experimental evidence that when a photon strikes an electron, the latter has a recoil with momentum proportional to $h/\lambda$ , where is h is Planck's constant.

It is at this point that Heisenberg introduces objective indeterminacy into the thought experiment. He writes that "the recoil cannot be exactly known, since the direction of the scattered photon is undetermined within the bundle of rays entering the microscope". In particular, the electron's momentum in the x direction is only determined up to $\delta p_x \approx \frac{h}{\lambda} sin (\epsilon/2)$. Combining the relations for $\delta x$ and $\delta p_x$ , we thus have that $\delta x \cdot \delta p_x \approx (\frac{\lambda}{sin(\epsilon/2)}) (\frac{h}{\lambda} sin(\epsilon/2)) = h$ , which is an approximate expression of Heisenberg's uncertainty principle.