Induction is the process in which an emf is induced by changing magnetic flux. Transformers, for example, are designed to be particularly effective at inducing a desired voltage and current with very little loss of energy to other forms (see our Atom on "Transformers. ") Is there a useful physical quantity related to how "effective" a given device is? The answer is yes, and that physical quantity is called inductance.
Mutual Inductance
Mutual inductance is the effect of Faraday's law of induction for one device upon another, such as the primary coil in transmitting energy to the secondary in a transformer. See , where simple coils induce emfs in one another.
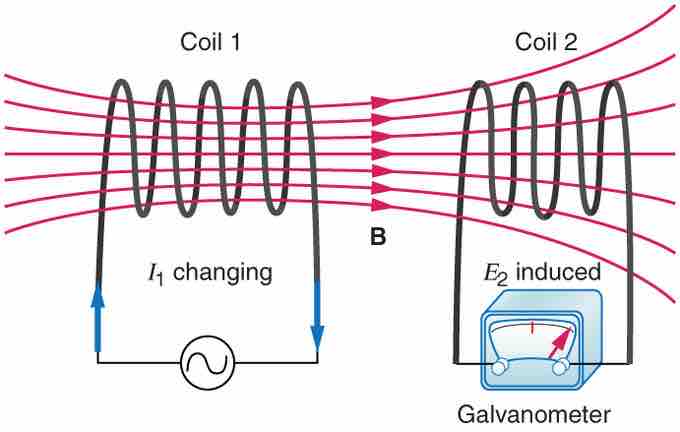
Mutual Inductance in Coils
These coils can induce emfs in one another like an inefficient transformer. Their mutual inductance M indicates the effectiveness of the coupling between them. Here a change in current in coil 1 is seen to induce an emf in coil 2. (Note that "E2 induced" represents the induced emf in coil 2. )
In the many cases where the geometry of the devices is fixed, flux is changed by varying current. We therefore concentrate on the rate of change of current, ΔI/Δt, as the cause of induction. A change in the current I1 in one device, coil 1, induces an EMF2 in the other. We express this in equation form as
where M is defined to be the mutual inductance between the two devices. The minus sign is an expression of Lenz's law. The larger the mutual inductance M, the more effective the coupling.
Nature is symmetric here. If we change the current I2 in coil 2, we induce an emf1 in coil 1, which is given by
where M is the same as for the reverse process. Transformers run backward with the same effectiveness, or mutual inductance M.
Self-Inductance
Self-inductance, the effect of Faraday's law of induction of a device on itself, also exists. When, for example, current through a coil is increased, the magnetic field and flux also increase, inducing a counter emf, as required by Lenz's law. Conversely, if the current is decreased, an emf is induced that opposes the decrease. Most devices have a fixed geometry, and so the change in flux is due entirely to the change in current ΔI through the device. The induced emf is related to the physical geometry of the device and the rate of change of current. It is given by
where L is the self-inductance of the device. A device that exhibits significant self-inductance is called an inductor. Again, the minus sign is an expression of Lenz's law, indicating that emf opposes the change in current.