The electric field of a point charge is, like any electric field, a vector field that represents the effect that the point charge has on other charges around it. The effect is felt as a force and when charged particles are not in motion this force is known as the electrostatic force. The electrostatic force is, much like gravity, a force that acts at a distance. Therefore, we rationalize this action at a distance by saying that charges create fields around them that have effects on other charges.
Given a point charge, or a particle of infinitesimal size that contains a certain charge, electric field lines emanate radially in all directions. If the charge is positive, field lines point radially away from it; if the charge is negative, field lines point radially towards it.
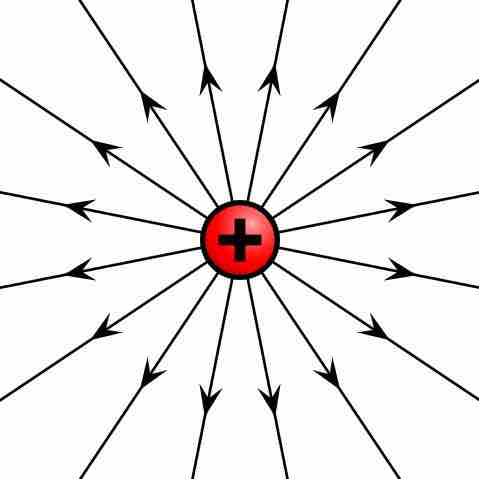
Electric field of positive point charge
The electric field of a positively charged particle points radially away from the charge.
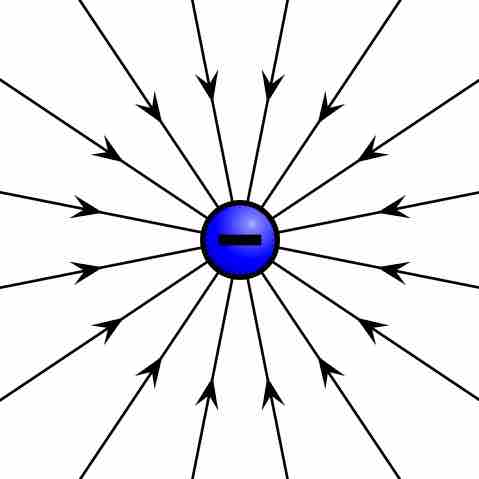
Electric field of negative point charge
The electric field of a negatively charged particle points radially toward the particle.
The reason for these directions can be seen in the derivation of the electric field of a point charge. Let's first take a look at the definition of electric field of a point particle:
In the above equation, q represents the charge of the particle creating the electric field and the constant k is a result of simply lumping the constants together. This charge is either positive or negative. If the charge is positive, as shown above, the electric field will be pointing in a positive radial direction from the charge q (away from the charge) and the following text explains why. The above equation is defined in radial coordinates which can be seen in .
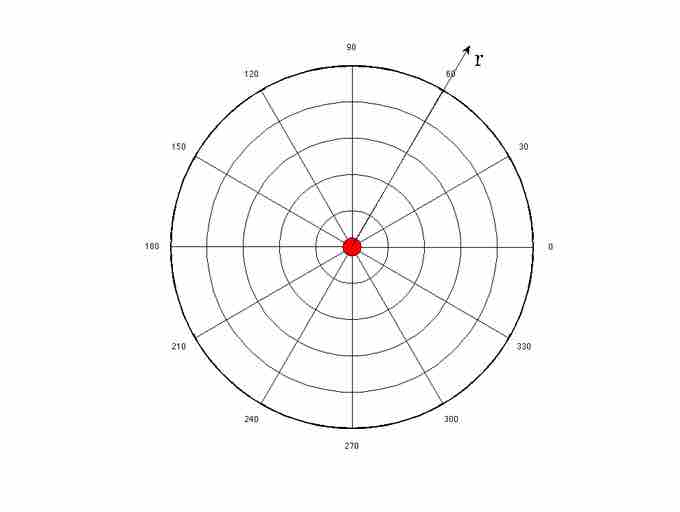
Radial Coordinate System
The electric field of a point charge is defined in radial coordinates. The positive r direction points away from the origin, and the negative r direction points toward the origin. The electric field of a point charge is symmetric with respect to the θdirection.
If we now place another positive charge, Q (called the test charge), at some radial distance, R, away from the original particle, the test charge will feel a force given by
The thing to keep in mind is that the force above is acting on the test charge Q, in the positive radial direction as defined by the original charge q. This means that because the charges are both positive and will repel one another, the force on the test charge points away from the original charge.
If the test charge were negative, the force felt on that charge would be
Notice that this points in the negative